ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
 |
Московский государственный университет
Приборостроения и информатики

Кафедра высшей математики
Выборнов А.Н.
ПОСОБИЕ ПО МАТЕМАТИКЕ
Часть 1
Основы линейной алгебры
Москва 2015
Матрицы.
Матрицей называется прямоугольная таблица чисел 
В этой матрице k строк и n столбцов. (Матрица (k x n) – размер). Двойной индекс принято писать без разделителей, читается:  - «a один, два». Матрицы мы будем обозначать большими латинскими буквами.
- «a один, два». Матрицы мы будем обозначать большими латинскими буквами.
Примеры матриц:
1) А=  3) С=
3) С=  - столбец, т.е. матрица (3x1)
- столбец, т.е. матрица (3x1)
2) B= 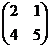 4) D=
4) D=  - строка (1x4)
- строка (1x4)
Матрица – квадратная, если число строк равно числу столбцов.
Линейные операции над матрицами.
Линейные операции – это сложение, вычитание, умножение на число.
Термин «линейный» связан с тем, что прямая линия на плоскости задаётся, так называемым, линейным уравнением (см. ниже).
Сложение и вычитание матриц.
Складывать можно только матрицы одинакового размера. Эта операция выполняется поэлементно, т.е. складывают элементы с одинаковыми индексами. Аналогично происходит операция вычитания матриц.
А=  , B=
, B= 

Пример:  +
+  =
= 
Умножение на число.
При умножении матриц на число все её элементы умножаются на это число.

Пример: 
Линейные операции над матрицами обладают очевидными свойствами, легко следующими из соответствующих свойств арифметических операций над действительными числами:
1) A+B= B+A
2) (A+B) +C=A+(B+C)
3) 
4) 
5) 
(свойства выполнимы для любых матриц А, В, С и любых действительных чисел  для которых определён результат написанных операций).
для которых определён результат написанных операций).
Замечание. Как видно, в линейных операциях прямоугольная двухмерная структура матриц не имеет роли, здесь используются только то, что в матрицах каждый элемент имеет однозначно определённое место.
Транспонирование матриц.
Операция транспонирования меняет местами строки и столбцы, превращая матрицы размера (kxn) в матрицы (nxk).
Примеры:
1) 
2) 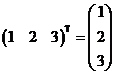
3) 
Очевидно, что для любой матрицы А выполнено равенство 
Умножение матриц.
Замечание. Так исторически сложилось, что этим термином «умножением» названа весьма специфическая операция, а не (ожидаемая по аналогии со сложением матриц) операция поэлементного умножения. Тем не менее, есть ряд причин оправдывающих использование слова «умножение». См. ниже.
Определим сначала умножение строки на столбец.
Пусть  , тогда
, тогда  - число (или матрица (1x1)).
- число (или матрица (1x1)).
Перейдём к общему случаю.
Перемножать можно только матрицы согласованного размера и в определённом порядке.
Произведение матриц АВ определено только в случае когда длина строки матрицы А равна длине столбца матрицы В, т.е. А- матрица (kx n), B- матрица (n x l).
Матрицу А будем писать, как набор строк, а матрицу В, как набор столбцов.

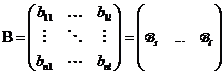
Тогда матрица АВ будет иметь размер (kx l)

Примеры:
1)
 (2x2), (2x2).
(2x2), (2x2).
В этом случае определены оба произведения АВ и ВА.
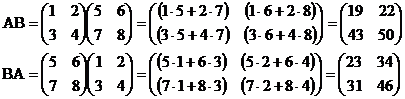
Как видим АВ  ВА – порядок умножения существенен даже для квадратных матриц одинакового размера.
ВА – порядок умножения существенен даже для квадратных матриц одинакового размера.
Замечание. Бывает, что для квадратных матриц АВ=ВА, тогда говорят, что матрицы А и В коммутируют.
2)


Пример умножения квадратной матрицы на столбец:
3)  здесь умножение в обратном порядке неосуществимо, как и в следующем примере умножения строки на квадратную матрицу:
здесь умножение в обратном порядке неосуществимо, как и в следующем примере умножения строки на квадратную матрицу:
4) 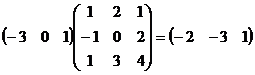

Операция умножения матриц обладает следующими свойствами:
1) (АВ)С=А(ВС) (ассоциативность)
2) (А 
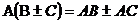
3) 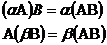
4) 
Свойства имеют место для любых матриц А,В,С и чисел  , для которых выполняются все записанные операции.
, для которых выполняются все записанные операции.
Единичная матрица.
Среди квадратных матриц размера n x n, есть матрица, которая ведёт себя по отношению к операции умножения как единица среди действительных чисел. Т.е. умножение на такую матрицу не меняет умножаемую матрицу.
Такая матрица называется единичной и обозначается буквой I (размер матрицы обычно виден из контекста).
Пример:
1)  2)
2) 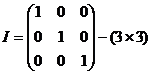 и т.д.
и т.д.

Имеет место следующее утверждение:
Утверждение. Для любых (не обязательно квадратных) матриц А и В, для которых определены АI и IB, будут выполнены равенства: AI=A и IB=B.
Таким образом, единичная матрица ведёт себя как единица, при умножении её на любую матрицу, на которую её можно умножить справа или слева.
Замечание. Среди матриц (n x n) существуют только одна матрица, удовлетворяющая свойствам приведённого утверждения, а именно указанная матрица I.
Действительно, если бы их было две  и
и  , следовательно
, следовательно 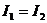 .
.
Определители.
Приступим к определению важного понятия определителя. Его роль проявится по мере дальнейшего изучения курса математики.
Замечание. Впервые понятие определителя появилось в работе великого учёного Г.Лейбница, которая была опубликована в 1684 году. В ней рассматривалось условие совместности трех уравнений с двумя неизвестными. Но систематически определители начали изучаться на полвека позже в работах Крамера и Вандермонда.
Определитель (или детерминант) – это число, связанное с квадратной матрицей А, обозначение: 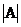 или det A.
или det A.
1. Определители 1-го порядка для матрицы А=  (1x1): det A=
(1x1): det A=  2. Определитель 2-го порядка:
2. Определитель 2-го порядка:  , det A=
, det A= 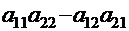
3. Определитель 3-го порядка: А=  ,
,
det A= 
4. Определитель 4-го порядка состоит из 4! «четыре факториал» =  произведений, в каждом произведении 4 сомножителя, являющихся элементами матрицы, из которых никакие два не стоят в одной строке и одном столбце.
произведений, в каждом произведении 4 сомножителя, являющихся элементами матрицы, из которых никакие два не стоят в одной строке и одном столбце.
Половина произведений берётся со знаком «+», другая половина со знаком «-», по некоторому правилу, которое мы не будем здесь излагать.
Определитель k-того порядка также состоит из 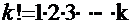 произведений, каждое из которых включает в себя k сомножителей.
произведений, каждое из которых включает в себя k сомножителей.
Функция k! растёт очень быстро:

…
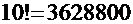
Поэтому прямое вычисление определителя высокого порядка даже с помощью вычислительной техники, очень трудоёмкая задача.
Если матрица записана в прямых чертах, то это обозначает определитель матрицы.
Пример:

Говоря о строках или столбцах определителя, имеют в виду строки или столбцы соответствующей матрицы.
Свойства определителей.
1. При перемене местами любых двух строк определитель меняет знак на противоположный.
2. При умножении всех элементов любой строки на некоторое число, определитель умножается на это число.
3. Если любую строку определителя разбить в сумму двух строк, то определитель можно представить как сумму соответствующих определителей:

4. Определитель, имеющий две одинаковые строки равен нулю. (Это свойство следует из свойства 1.).
5. Определитель, содержащий строку из нулей, равен нулю. (Это свойство следует из свойства 2.).
6. К любой строке определителя можно прибавить любую другую строку, умноженную на любое число. Определитель при этом не меняется. (Это свойство следует из свойств 2., 3., 4.).
7. Транспонирование не меняет определителя:


Ввиду свойства 7., т.к. транспонирование меняет строки со столбцами, все свойства 1.-6. выполнены и для столбцов определителя.
Указанные свойства легко проверяют для определителей 2-го порядка, но имеют место для определителей любого порядка.
Правило разложения определителя по строке (столбцу).
Это правило сводит вычисление определителя n-го порядка к вычислению нескольких определителей (n-1)-го порядка.
Дадим предварительные определения. Рассмотрим определитель n-го порядка.

Дополнительным минором (обозн.  ) к элементу
) к элементу  называется определитель, полученный из исходного вычёркиванием той строки и того столбца, в которых стоит элемент
называется определитель, полученный из исходного вычёркиванием той строки и того столбца, в которых стоит элемент  .
.
Например, рассмотрим определитель 3-го порядка. 
Тогда 
Замечание. Вообще, минором k-того порядка в матрице называется определитель, состоящий из элементов, стоящих на пересечении каких-то выбранных k строк и k столбцов. В рассмотренном выше примере 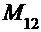 состоит из элементов, стоящих на пересечении 1-ой, 3-й строки и 2-го, 3-го столбца:
состоит из элементов, стоящих на пересечении 1-ой, 3-й строки и 2-го, 3-го столбца:

Алгебраическим дополнением к элементу  называется число
называется число  , т.е.
, т.е.  , если (i+j) – чётное число, и
, если (i+j) – чётное число, и
 , если (i+j) – нечётное.
, если (i+j) – нечётное.
Следующая схема показывает, какие знаки нужно брать пред минором, для определителей 3-го порядка: 
Теорема (правило разложения определителя).
Сформируем для определителя 3-го порядка.
 (по 1-ой строке)=
(по 1-ой строке)=
= 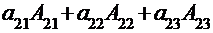 (по 2-ой строке)= =
(по 2-ой строке)= = 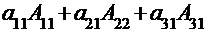 (по 1-му столбцу).
(по 1-му столбцу).
Таким образом, при вычислении определителя можно элементы выбранной (любой) строки (столбца) умножить на алгебраические дополнения к этим элементам и результаты сложить.
Правило выполнено для определителя любого порядка, начиная со второго.
Замечание. Рассмотрим  . Тогда
. Тогда 

 , как и должно быть.
, как и должно быть.
Замечание. Правило разложения определителя по строке (столбцу) иногда принимают за определение, и дальше теорию определителей строят индуктивно, определив определители 1-го порядка, затем, используя правило, определители 2-го порядка, затем 3-го и т.д.
Пример.

Определители и умножение матриц.
Имеет место следующая теорема:
Теорема. Если А и В – две квадратные матрицы одинакового размера, то
 .
.
Т.е. определитель произведения матриц равен произведению их определителей.
Замечание. Вот и аргумент (не единственный), оправдывающий термин “произведение” для введённой операции над матрицами.
Обратная матрица.
Будем рассматривать квадратные матрицы nxn.
Заметим, во-первых, что det I=1.
Утверждение. Определитель единичной матрицы (любого размера) равен единице.
Доказательство проведём для матрицы 3x3, но оно, очевидно, проходит по той же схеме и для единичной матрицы любого размера.
Используем разложение по 1-ой строке:
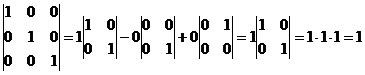
Замечание. Таким же образом доказывается, что определитель диагональной матрицы (у которой все элементы, кроме, может быть, элементов главной диагонали, равны нулю) равен произведению элементов, стоящих на главной диагонали:

Определение. Рассмотрим квадратную матрицу А, размером (nxn). Матрица  называется обратной для А, если
называется обратной для А, если 
Замечание. Понятие обратной матрицы позволяет организовать в квадратных матрицах, что-то вроде деления (это умножение на обратную). Сравните для чисел: 
Определение. Матрица А называется обратимой, если существует  .
.
Замечание. Не все числа обратимы. (Правда, почти все: только ноль необратим). Так и не все матрицы обратимы.
Утверждение. Если А обратима, то det A 
Доказательство:
 det A
det A  и det
и det 
Определение. Матрица А, для которой det A=0 называется вырожденной, а для которой  (естественно) невырожденной.
(естественно) невырожденной.
Замечание. Термин «вырожденная матрица» связан с понятием вырожденного линейного преобразования (оператора). Мы будем рассматривать это понятие позже в нашем курсе.
Итак обратимая матрица обязательно невырожденна. Оказывается, верно и обратно: всякая невырожденная матрица обратима.
ТЕОРЕМА
Рассмотрим квадратную матрицу А,  .
.
Если det A  , то существует обратная матрица
, то существует обратная матрица  , причём
, причём  может быть найдена следующим образом:
может быть найдена следующим образом:

где  - это матрица, состоящая из алгебраических дополнений, к элементам матрицы А.
- это матрица, состоящая из алгебраических дополнений, к элементам матрицы А.
Здесь мы должны вычислить  определителей (n-1)-го порядка.
определителей (n-1)-го порядка.
Замечание. Есть и другие способы нахождения обратной матрицы, помимо приведённой формулы. Но всегда, задача обращения матрицы высокого порядка- это трудоёмкая задача.
Замечание: Для обратной матрицы А существует только одна обратная. Действительно, если бы их было две:  и
и 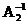 ,то
,то 
Примеры:
1)  det A=2,
det A=2, 

2)  det A=
det A= 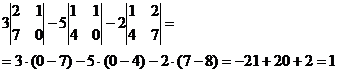


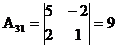


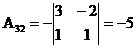




Пример: Решить матричное уравнение АХ = В, где

 3 5 -3 7
3 5 -3 7
А = 1 2; В = 0 2; Х – неизвестная матрица 2х2.

 2 -5
2 -5
Решение: Заметим, что det = 1 = 0, поэтому существует  = -1 3.
= -1 3.
Умножим равенство АХ = В слева на 
АХ = В ó  (AX) =
(AX) =  B ó
B ó
( A)X =
A)X =  B ó
B ó
I X =  B ó
B ó
X =  B
B


 2 -5 -3 7 -6 4
2 -5 -3 7 -6 4
X = -1 3 0 2 = 3 -1.
Пример: Решить матричное уравнение ХА = В, где
 2 1 -3
2 1 -3
А = 1 1 1; В = (6 4 -3); Х – неизвестная строка 1х3.
3 2 -1
Решение: Используем обратную матрицу.





 1 1 1 1 1 1
1 1 1 1 1 1
det A = 2 2 -1 - 3 -1 - 3 3 2 = 2(- 3) – (- 4) – 3(- 1) =








 1 1 1 -3 1 -3
1 1 1 -3 1 -3





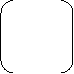
 A11 = 2 -1 = - 3 A21 = - 2 -1 = - 5 A31 = 1 1 = 4
A11 = 2 -1 = - 3 A21 = - 2 -1 = - 5 A31 = 1 1 = 4
1 1 2 -3 2 -3
A12 = - 3 -1 = 4 A22 = 3 -1 = 7 A32 = - 1 1 = - 5





 1 1 2 1 2 1
1 1 2 1 2 1
 A13 = 3 2 = - 1 A23 = - 3 2 = - 1 A33 = 1 1 = 1
A13 = 3 2 = - 1 A23 = - 3 2 = - 1 A33 = 1 1 = 1
-3 -5 4
 = 4 7 -5
= 4 7 -5
-1 -1 1
XA = B ó (XA)  = B
= B  ó X(A
ó X(A  ) = B
) = B  ó XI = B
ó XI = B  ó
ó
 X = B
X = B 
-3 -5 4
X = (6 4 -3) 4 7 -5 = (1 1 1).
-1 -1 1
Системы линейных уравнений.
Опр. Система к линейных уравнений с n неизвестными:
 а11 х1 + а12 х2 + … + а1n xn = b1
а11 х1 + а12 х2 + … + а1n xn = b1
a21 x1 + a22 x2 +... + a2n xn = b2
......
ak1 x1 + ak2 x2 +... + akn xn = bk, где аij – коэффициенты системы, bi – свободные члены, хj – неизвестные.
Матричная запись системы.
Рассмотрим матрицы:
 a11 … а1n
a11 … а1n
А = ..... – матрица коэффициентов (её называют матрицей системы),
ak1... akn
 b1
b1
В = .. – столбец свободных членов,
bk
 х1
х1
Х = .. – столбец неизвестных.
хn
Система теперь может быть записана в виде матричного уравнения:
АХ = В.






