При выборе методов анализа чувствительности следует иметь ввиду, что в большинстве случаев зависимости выходных показателей объектов от входных параметров задаются в неявном виде. Численные методы анализа чувствительности применяются при условии непрерывности и дифференцируемости этих зависимостей.
Универсальным методом расчета коэффициентов чувствительности является метод приращений, который основан на численном дифференцировании зависимостей yj (xj) в некоторой точке Х0:
 ,
,
где D xi – малое приращение i -го параметра.
Для определения всех элементов матрицы чувствительности aij необходимо выполнить 2 m расчетов выходных показателей при различных значениях входных параметров.
Статистический анализ
Входные параметры могут получать случайные значения, причем их распределение следует определенному закону.
Метод наихудшего случая. Определяются предельные отклонения выходных показателей, наблюдающиеся при самых неблагоприятных сочетаниях предельных отклонений параметров в границах их изменения.
Подобные оценки предельных отклонений выходных показателей дают лишь грубое приближение к действительно наблюдаемым отклонениям, что вызывается неучетом вероятностной природы формирования погрешностей параметров. Например, для случая наиболее распространенного нормального распределения случайных значений параметров вероятность появления граничного значения параметра составляет не более 0,135%, а для совокупности взаимно независимых параметров эта вероятность значительно уменьшается.
Вероятностный метод статистического анализа основан на применении операции дисперсии к уравнениям математической модели объекта yj = fj (x 1,..., xi,..., x m); j = 1,..., n:
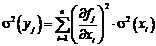 ,
,
где s(yj) и s(xi) – средние квадратичные отклонения соответственно выходных показателей и входных параметров; ∂ fj /∂ xi –коэффициент чувствительности при средних значениях всех параметров.
Вероятностный метод дает возможность определить средние значения (математическое ожидание) выходных показателей по средним значениям параметров и рассчитать средние квадратичные отклонения yj по средним квадратичным отклонениям xi при следующих условиях:
- все параметры являются взаимно независимыми случайными величинами;
- погрешности параметров и показателей подчинены нормальному распределению вероятностей;
- математическая модель объекта анализа линейна или может быть принята таковой при реальных отклонениях xi от номинальных значений.
Сущность метода статистических испытаний состоит в воспроизведении случайных значений входных параметров с последующим расчетом показателей объекта, соответствующих этим параметрам. По завершении некоторого числа таких расчетов статистическая обработка полученных значений по каждому показателю дает необходимую информацию о характере распределения этих значений. В данном случае на математическое описание объекта не накладывается ограничений по явновыраженности, дифференцируемости и линейности.
Чем больше число испытаний, тем более точную информацию удается получить. Применение метода статистических испытаний немыслимо без использования ЭВМ.






