УСЛОВИЯ ЗАДАЧ ПО РАДИОСИСТЕМАМ УПРАВЛЕНИЯ СТАЦИОНАРНЫМИ C ПУТНИКАМИ СВЯЗИ
Условия задачи 6.1
Пояснить принцип управления моментами излучения сигналов наземных станций методом опорного сигнала в системе связи через стационарный спутник с глобальными антеннами при многостанционном доступе с временным разделением (МДВР) сигналов наземных станций.
Условия задачи 6.2
Определить ширину диаграммы направленности антенны стационарного спутника связи с глобальным лучом. Обеспечивает ли система связи на основе таких спутников связь на всей поверхности Земли? Если нет, то тогда определить зону поверхности Земли, где такая связь не обеспечивается. Предложить модификации орбит спутников, которые бы обеспечили связь на всей поверхности Земли.
Условия задачи 6.3
Определить среднее расстояние между стационарным спутником связи и земной станцией, расположенной на северной широте φ = 50º и долготе, отличающейся от долготы точки стояния стационарного спутника на Δλ = 40º. Определить диапазон изменения этого среднего расстояния и диапазон изменения радиальной скорости движения стационарного спутника относительно земной станции при условии, что эксцентриситет орбиты спутника равен 
, а наклонение 
плоскости его орбиты стационарного к плоскости экватора равно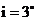 
,
Условия задачи 6.4
Определить московское время входа 
стационарного спутника, имеющего долготу точки стояния 30º восточной долготы, в тень Земли и выхода 
его из этой тени ежегодно 2 апреля.
Условия задачи 6.5
Земная станция находится на северной широте 30º и долготе, отличающейся от долготы точки стояния стационарного спутника на Δλ = 30º. Определить максимальную длительность и дату перерыва в связи 
этой станции через стационарный спутник, вызываемого прохождением стационарным спутником диска Солнца. Ширина диаграммы направленности антенны земной станции 2º30′.
РЕШЕНИЯ ЗАДАЧ ПО РАДИОСИСТЕМАМ УПРАВЛЕНИЯ СТАЦИОНАРНЫМИ СПУТНИКАМ СВЯЗИ
Решение задачи 6.1
На рисунке 6.1.1 показан пример образования кадра сигнала на входе приёмника стационарного спутника из сигналов, излучаемых станциями в направлении на стационарный спутник. Из рисунка 6.1.1 видим, что для реализации многостанционного доступа с временным разделением (МДВР) моменты начала излучения сигналов разных станций должны учитывать удаление этих станций от стационарного спутника. Например, третья станция на рис. 6.1.1 расположена к стационарному спутнику ближе, чем вторая. Но групповой сигнал третьей станции должен поступать на вход ретранслятора после сигнала второй станции. Этого можно добиться задержкой излучения третьей станции относительно второй.
Для временной синхронизации работы станций в системах связи через стационарный спутник с глобальными антеннами и МДВР получил распространение метод опорного сигнала. Идея этого метода иллюстрируется рисунком 6.1.2 а и б. В методе опорного сигнала одна из передающих станций, называемая ведущей, излучает периодический опорный сигнал, совмещаемый по времени с сигналом кадровой синхронизации. Этот сигнал ретранслируется стационарным спутником и принимается всеми остальными передающими станциями. На рисунке 6.1.2 а и б символы 
, 
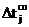, указанные над осью времени t, обозначают времена распространения опорного сигнала от ведущей станции до стационарного спутника и от стационарного спутника до j-й передающей станции соответственно.
Каждая передающая станция так же излучает на спутник свой сигнал кадровой синхронизации и принимает его после переизлучения со спутника. На рисунке 6.1.2 а и б символы 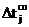, указанные под осью времени t, обозначают времена распространения сигнала кадровой синхронизации от j-й передающей станции до стационарного спутника и обратно. Моменты времени излучения сигналов кадровой синхронизации j-й передающей станцией на рисунках 6.1.2 а и б показаны жирными точками. В процессе осуществления синхронизации каждая j-я передающая станция путём изменения положения начала кадра (положение жирных точек на оси времени) стремится свести к нулю интервал времени между моментами приёма опорного сигнала ведущей станции и своего ретранслированного сигнала кадровой синхронизации. Этот интервал времени выделен на рисунке 6.1.2 а фигурными скобками и обозначен символами 
. После сведения интервала времени к нулю, возникает ситуация, показанная на рисунке 6.1.2 б.
Рисунок 6.1.1 Взаимное расположение во времени сигналов разных станций для обеспечения их временного разделения в бортовой аппаратуре стационарного спутника
Сигнал, излучаемый j-й передающей станцией в моменты времени, обозначенные на рис. 6.1.2 б жирными точками будет достигать стационарного спутника в моменты начала кадра на входе ретранслятора. Для того, чтобы сигнал j-й передающей станции достигал стационарного спутника в моменты времени, выделенные в кадре для этой станции, его необходимо сместить относительно начала кадра на станции (жирные точки на рис. 6.1.2 б) на величину смещения 
сигнала рассматриваемой станции относительно начала кадра. Эти смещения определяют положение временных интервалов, выделяемых разным станциям в кадре, показанном на рис. 6.1.3.
Рисунок 6.1.2 Распространение сигналов в методе синхронизации по опорному сигналу
Рисунок 6.1.3 Структура кадра группового сигнала, поступающего на вход ретранслятора
Решение задачи 6.2
Для решения поставленной задачи будем использовать идеальную орбиту стационарного ИСЗ, т. е. полагать, что ИСЗ неподвижно висит над определенной точкой экватора Земли. Для выполнения этого условия, необходимо, чтобы угловая скорость вращения ИСЗ вокруг Земли была бы равна угловой скорости вращения самой Земли. Для этого требуется, чтобы период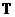 
обращения спутника вокруг Земли, был бы равен длительности сидерических (звёздных) суток. Под сидерическими сутками понимается период обращения Земли вокруг своей оси относительно звёзд. Этот интервал времени несколько меньше, чем средние солнечные сутки, доля которых (
) принята в качестве секунды, как единицы измерения времени. Период обращения Земли вокруг своей оси относительно звёзд короче того же периода обращения относительно Солнца потому, что за одни солнечные сутки Земля совершает один оборот вокруг своей оси (т. е. относительно звёзд) плюс дополнительную часть оборота (относительно звёзд), поскольку она так же проходит за это же время ещё ~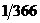 
часть своего пути по орбите вокруг Солнца. Длительность сидерических суток равна 
(
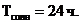). Т. е. сидерические сутки приблизительно на 4 минуты короче среднесолнечных. Отличие в длительности среднесолнечных и сидерических суток можно пояснить так же следующим образом. В результате движения Земли вокруг Солнца, наблюдаемое с поверхности Земли количество оборотов, которое звёзды делают за год вокруг Земли, на единицу больше, чем наблюдаемое с поверхности земли количество оборотов Солнца за тот же период. (
).
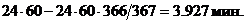Из формулы 2.26, приведенной на стр. 89 в учебнике [1], нетрудно получить следующее выражение для вычисления радиуса идеальной орбиты стационарного спутника по его периоду обращения 
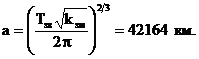(6.2.1)
где 
‑ гравитационный параметр Земли.
Учитывая, что средний радиус Земли равен ~6378 км., получаем, что высота идеальной орбиты стационарного спутника равна 
(экваториальный радиус Земли 6378.165 км.) больше её полярного радиуса (6356.785 км.) на 21.4 км.). Плоскость идеальной орбиты стационарного ИСЗ строго совпадает с плоскостью экватора Земли.
Из очевидных соотношений, представленных на рисунке 6.2.1, следует, что ширина диаграмы направленности антенны стационарного спутника с глобальным лучом равна 
, а максимальная широта видимости 
Рисунок 6.2.1 Определение ширины диаграмм направленности антенны 2α и максимальной широты β видимости стационарного спутника
Из рис. 6.2.1 видим, что диаграмма направленности антенны стационарного спутника связи с глобальным лучом охватывает область Земли ±81.3° по широте и 162.6° по долготе. Для охвата всех возможных долгот на поверхности Земли в системе связи необходимо использовать три стационарных спутника, показанных на рис. 6.2.2. Но даже в этом случае полярные области Земли южнее 81.3° южной широты и севернее 81.3° северной широты не охватываются такой системой связи.
Для того, чтобы обеспечить видимость спутника связи с Северного и Южного полюсов Земли или просто расширить зону обслуживания до более высоких (северных) и низких (южных) широт, плоскость орбиты стационарного спутника можно намеренно сделать наклонной к плоскости экватора Земли. Такие орбиты называются геосинхронными. Вследствие наклонения орбиты стационарного спутника к плоскости экватора подспутниковая точка непрерывно перемещается по трассе похожей на восьмёрку. На рисунке 6.2.3 показаны трассы движения подспутниковой точки для геосинхронных (24-часовых) идеальных круговых орбит при разных углах наклонения, включая случай идеальной геостационарной и полярной орбиты.
Рисунок 6.2.2 Схема размещения трёх спутников связи на геостационарной орбите для глобального покрытия
Для идеальной геостационарной орбиты трасса движения подспутниковой точки вырождается в точку на экваторе Земли. В случае полярной геосинхронной орбиты трасса в районе экватора вырождается в прямую линию.
Рисунок 6.2.3 Геосинхронные (24-часовые) орбиты спутников Земли (а) и трассы движения подспутниковой точки (б)
Если на наклонной геосинхронной орбите равномерно разместить три (показаны на рис. 6.2.3) или более спутников, то в любой момент времени из точки расположения северного либо южного полюса будет виден один из этих геосинхронных спутников. Система связи с такими орбитами охватывает всю поверхность Земли.
Решение задачи 6.3
Вычисление среднего расстояния 
для идеальной орбиты стационарного спутника связи иллюстрируется рисунком 6.3.1,
Рисунок 6.3.1 Вычисление среднего расстояния между земной станцией и стационарным спутником
где
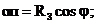
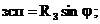(6.3.1)
и по теореме косинусов
(6.3.2)
Из (6.3.2) с учетом (6.3.1) получаем
(6.3.3)
Подставляя в (6.3.3) значения φ = 50º и Δλ = 40º получаем 
.
Наклонение орбиты к плоскости экватора и эксцентриситет отличные от нуля приводят к тому, что расстояние между земной станцией и стационарным спутником отклоняется от . Максимальные вариации дальности 
в км и радиальной скорости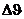 
в м/c, с которыми стационарный спутник движется относительно земной станции, могут быть вычислены с помощью диаграммы, представленной на рисунке 6.3.2 [6]. На этом рисунке по вертикальной оси отложена широта земной станции, а по горизонтальной оси разность между долготой земной станции и средней долготой точки расположения стационарного спутника.
Рисунок 6.3.2 Диаграмма для вычисления диапазонов изменения дальности и ΔR км и радиальной скорости 
м/с движения стационарного спутника относительно земной станции
Диаграмма построена для угла наклонения плоскости орбиты к плоскости экватора 
. Для других углов наклонения, отличных от 1о, величины, извлекаемые из диаграммы, следует умножать на величину угла наклонения, выраженную в градусах. Величину северной широты для станций, расположенных в южных широтах, следует определять как их южную широту с обратным знаком.
Для значений φ = 50º и Δλ = 40º, заданных по условию задачи 6.3 из диаграммы, представленной на рис. 6.3.2, получаем 
, 
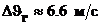. Учитывая, что наклон плоскости орбиты стационарного спутника к плоскости экватора по условию задачи равен 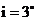, получаем 
, 
.
Отличный от нуля эксцентриситет е орбиты спутника, вызывает изменение расстояния между спутником и наблюдателем, находящимся на экваторе, на величину [6]
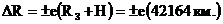(6.3.4)
Используя значение эксцентриситета орбиты спутника, заданное по условию задачи, получаем 
Решение задачи 6.4
Как видно из рисунка 6.4.1,а,б на интервале времени вблизи равноденствий стационарные спутники будут один раз в сутки входить в тень Земли.
Рис. 6.4.1 Геометрическая схема возникновения затенений стационарного спутника
и проекции шумового диска при движении Земли вокруг Солнца
Определение времени входа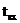 
стационарного спутника в тень Земли и времени выхода 
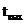его из этой тени в зависимости от времени года, осуществляется с помощью графика, показанного на рисунке 6.4.2 (график заимствован из [7]).
Рис. 6.4.2 График для определения времени входа стационарного спутника в тень Земли и
выхода из нее
По вертикальной оси графика на рисунке 6.4.2 откладывается московское время входа и выхода стационарного спутника из тени Земли, при условии, что долгота точки стояния спутника λ = 0о. Для долгот точек стояния 
, значения московского времени входа 
и 
могут быть вычислены по формуле
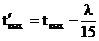(6.4.1)
где 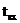и 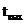определяются с помощью рисунка 6.4.2.
Из рис. 6.4.2 для даты 2 апреля, заданной в условии задачи, находим 
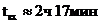или 
, 
или 
. Однако долгота точки стояния стационарного спутника по условию задачи равна 
. Поэтому для этой долготы осуществляем пересчет по формулам (6.4.1)
, 
(6.4.2)
Переход к иному не московскому времени осуществляется с учетом смещения часовых поясов.
Решение задачи 6.5
Как видно из рисунка 6.5.1а,б, на интервале времени вблизи равноденствий для наземных станций могут возникать перерывы в связи, вызываемые прохождением спутником диска Солнца. Это явление возникает тогда, когда углы наведения от земной станции на спутник и Солнце настолько близки, что спутник и солнце находятся в пределах ширины основного лепестка диаграммы направленности антенны земной станции.
В такой ситуации земная станция воспринимает Солнце как диск с очень малым угловым диаметром, равным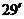 
(0.48o) и с чрезвычайно большой интенсивностью теплового шума, на фоне которого выделение сигнала стационарного спутника становится невозможным. Например, для больших антенн диаметром 30 м. на частоте 4 гГц угловое отклонение α электрической оси антенны земной станции от направления на центр Солнца, в пределах которого прием сигнала стационарного спутника является невозможным, приближённо равно α = 0.6о. Таким образом, для земной станции, долгота которой совпадает с долготой точки стояния стационарного спутника, Солнце соответствует шумовому диску с эффективным диаметром d, находящимся на расстоянии стационарного спутника от поверхности Земли, где d =2Ssinα ≈ 775 км., S ≈ 37·103 км. – дальность до стационарного спутника. Для антенн меньшего диаметра эффект прохождения спутником диска Солнца проявляется на большей территории, так как основной лепесток диаграммы направленности таких антенн шире и поэтому диск Солнца дольше находится в пределах этого лепестка. Например, если диаметр антенны равен 10 м., то на частоте 4 гГц требуемое угловое смещение α = 1о.
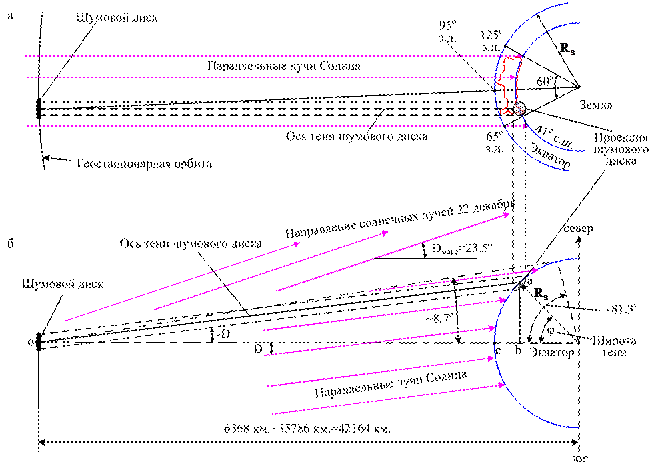
Рис. 6.5.1 Геометрическая схема образования проекции шумового диска на поверхности Земли, при прохождении стационарным спутником диска Солнца. Долгота точки стояния стационарного спутника 95o з. д.
На рисунке 6.5.1 показана проекция шумового диска на поверхность Земли (прохождение спутником диска Солнца). Склонение солнца относительно экватора Земли при этом равно ~ 6.5о. Северная широта центра проекции шумового диска равна ~ 41о.
Размер шумового диска d максимален для земных станций, долгота расположения которых равна долготе точки стояния стационарного спутника, и равен d = 2Ssinα. При отклонении долготы расположения земной станции от долготы точки стояния стационарного спутника на Δλ, максимальный размер шумового диска и проекции следует умножать на cosΔλ.
Время перерыва в связи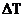 
- это время, за которое проекция шумового диска с диаметром d = 2Ssinα·cosΔλ проходит Земную станцию, или иными словами, Земля и вместе с нею стационарный спутник смещаются на угол 2α. Следовательно, если ширина диаграммы направленности антенны земной станции равна 2α=2о, то максимальное время перерыва связи для земной станции, долгота расположения которой отличается от долготы точки стояния стационарного спутника на Δλ=30о, будет равно
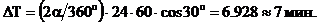(6.5.1)
Найдём связь между широтой центра проекции шумового диска и склонением солнца D. Из треугольника oab, показанного на рисунке 6.5.1б имеем:
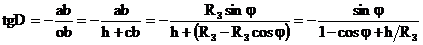(6.5.2)
На рисунке 6.5.2 показаны широты северной и южной границ проекции шумового диска в зависимости от угла склонения солнца D.
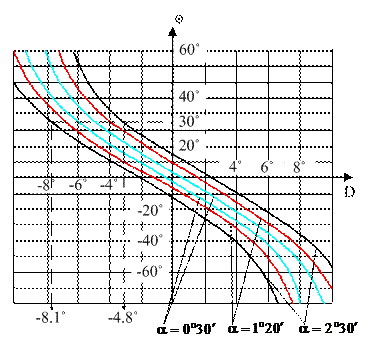
Рис. 6.5.2 Зависимость широты φ верхней и нижней границ проекции шумового диска,
от склонения Солнца D при различных углах α.
Параметром графиков, представленных на рисунке 6.5.2, является угловое смещение α электрической оси антенны земной станции от направления на центр Солнца, в пределах которого прием сигнала стационарного спутника невозможен. Графики были построены путем нахождения решения нелинейного уравнения, которое возникает при задании в выражении (6.5.2) определённого значения склонения солнца D. Для каждого D определялось значение широты земной станции φ, удовлетворяющей указанному уравнению. Далее вычислялись широты верхней и нижней границ области проекции шумового диска в зависимости от углового смещения α.
По условию задачи, земная станция находится на северной широте 30º. Из рис. 6.5.2 находим, что проекция шумового диска на поверхность земли при ширине диаграммы направленности антенны земной станции 2º30′ будет двигаться по поверхности Земли на северной широте в 30º в период времени, кода склонение Солнца будет изменяться в пределах от ≈ -8.1º до ≈ -4.8º. Конкретные значения дат в перерыве связи устанавливаются с помощью астрономического ежегодника как даты, в пределах которых склонение солнца будет изменяться в пределах от ≈ -8.1º до ≈ -4.8º.
