При вытеснении из пластов нефтей обычной водой нефтеотдача снижается с увеличением отношения вязкостей нефти и воды. При разработке нефтяных залежей с высоковязкими нефтями вода «находит» высокопроницаемые участки пласта (трещины, отдельные участки пласта с повышенной проницаемостью, вода прорывается вдоль кровли и подошвы пласта и т.п.) и прорывается по ним к забоям добывающих скважин, преждевременно обводняя их. Более того, так вода имеет гораздо меньшую вязкость в сравнении с нефтью, то она фильтруется гораздо быстрее чем нефть – вода неравномерно (как по вертикали так и по горизонтали) прорывается вглубь пласта образуя так называемые «гидродинамические языки». С течением времени эти «гидродинамические языки» смыкаются, оставляя позади фронта вытеснения нефти водой не затронутые процессом вытеснения участки пласта – «целики» нефти. Динамика образования гидродинамических языков в зависимости от соотношения вязкостей нефти и вытесняющего агента (воды, раствора ПАА и т.п.) представлена на рисунке 7.1
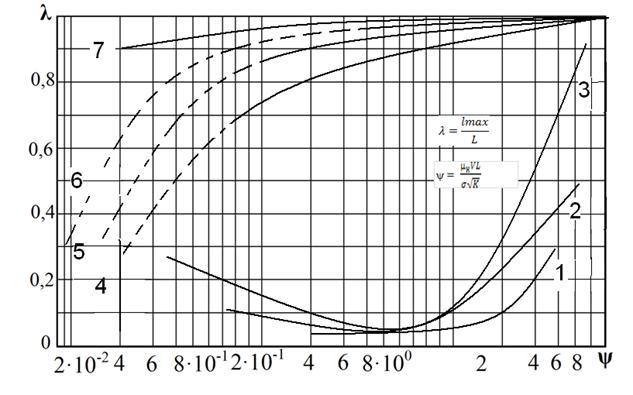
Рисунок 7.1 – Зависимость критерия устойчивости l от безразмерной скорости вытеснения Ѱ μн/ μв: 1-2; 2-5; 3-10; 4-13; 5-16; 6-19; 7-27.
На рисунке 7.1 изображены кривые зависимости максимальной длины гидродинамических языков от скорости фильтрации, представленной в безразмерных координатах
l=f(ѱ) (7.1)
Где:
l= lmax/L
Ѱ = μн VL/ s 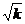
lmax– максимальная длина языков неустойчивости; L – длина модели пласта, μн - вязкость нефти, s - поверхностное натяжение на границе нефть –вода, V – скорость фильтрации, к – проницаемость.
Из рисунка видно, что для значений отношения вязкостей нефти и воды μ< 13, (μ=μн/μв) существует область устойчивого вытеснения нефти (значение l близко к пулю), т. е. длина языков неустойчивости очень мала (lmax» 0). При больших значениях μ (μ> 13) движение водонефтяного контакта становится неустойчивым – возникает вязкостная неустойчивость ( l»1). Все это приводит к резкому снижению безводной нефтедобычи и к увеличению водного периода вытеснения нефти и самое неблагоприятное к снижению коэффициента нефтеотдачи. Извлечение нефти в этот период происходит, с одной стороны, за счет расширения существующих и образования новых языков воды, и, с другой стороны, за счет «рассасывания» целиков нефти, оставшихся за фронтом вытеснения, под действием капиллярных сил. В этом случае для достижения удовлетворительной нефтеотдачи приходится добывать большое количество попутной воды (что очень затратно).
Для дальнейшего анализа данных приведенного рисунка обратимся к соотношению (7.1). Из него следует, что наиболее доступно управляемыми величинами для данной системы являются вязкость нефти μн и скорость фильтрации V. Следовательно, уменьшая скорость фильтрации при заданном значении параметра Ѱ, можно уменьшить скорости образования гидродинамических языков.
Однако, как следует из анализа промышленной практики и кривых (рисунок 7.1), устойчивое продвижение фронта вытеснения при «сверхмалых» скоростях удалось реализовать только при μ< 20 [9]. Скорости вытеснения, при которых удалось получить ровный фронт, оказываются весьма малыми, порядка 40—80 м/год – что недопустимо медленно [11].
Существование предельного значения отношения μн/ μв=μпред. после которого процесс вытеснения становится неустойчивым, объясняется тем, что при этом значении (μпред) отношение подвижности за фронтом и перед ним становится неблагоприятным. Предельное значение μпред зависит от фильтрационных свойств системы (пористая среда, нефть, вода), т. е. формы кривых относительных проницаемостей для данной системы, и обычно составляет величину от 7 до 15. Как указывалось выше, верхнее значение предельного отношения вязкостей может быть увеличено при реализации малых скоростей вытеснения.
Обращаясь к 7.1 легко определить, что увеличив вязкость вытесняющего агента (воды) можно добиться снижения соотношения вязкости нефти и вытесняющего ее агента.
Для уменьшения этого отношения и, следовательно, увеличения нефтеотдачи закачивают в нефтяные пласты водные растворы полимеров (чаще применяют полиакриламид ПАА).
Молекулы ПАА состоят из атомов углерода, водорода и азота. В определенных условиях молекула полимера представляет собой цепочку, длина которой соизмерима с размерами пор пласта [8]. Молекулы полимера в водном растворе, продвигаясь в пористой среде, сорбируются на зернах поверхности пород, (как бы «цепляются» за зерна этой среды), создавая дополнительное фильтрационное сопротивление [8].
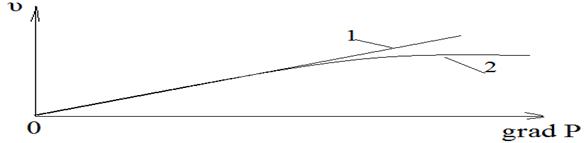
Pисунок 7.2 – Зависимость скоростей фильтрации воды и дилатантной жидкости от градиента давления grad р
При фильтрация водного раствора полимеров с увеличением градиента давления скорость его движения возрастает все медленнее по сравнению со скоростью воды по закону Дарси. Жидкость, скорость фильтрации которой нелинейно зависит от градиента давления и, притом, с каждым приращением градиента давления она возрастает на все меньшую величину, называется дилатантной. На рисунке 7.2 показана зависимость скорости фильтрации от градиента давления для обычной воды (кривая 1) и для водного раствора полимера (кривая 2). Формулу закона фильтрации водного раствора ПАА можно представить при n<1в виде:
 (7.1)
(7.1)
где μвп - вязкость водного раствора полимера.
С учетом фактора сопротивления R эту формулу записывают так:
 (7.2)
(7.2)
Если прокачивать водный раствор ПАА через пористую среду, то перепад давления возрастает более существенно, чем это следует из закона Дарси. Фильтрация водного раствора ПАА сопровождается его сорбцией пористой средой. При незначительных концентрациях полимера можно с определенным приближением пользоваться изотермой Генри.
Считается, что водный раствор ПАА целесообразно использовать для вытеснения нефти из пластов при ее вязкости от 10 до 30 мПа∙с.
В результате сорбции ПАА пористой средой в процессе вытеснения нефти образуется фронт сорбции. Впереди фронта сорбции полиакриламида в пласте движется вода, практически очищенная от него. Картина вытеснения нефти из пласта водным раствором ПАА аналогична таковой при вытеснении нефти с помощью ПАВ (но механизмы вытеснения совершенно различны). Расчеты по вытеснению нефти водным раствором ПАА можно провести по методике, изложенной для вытеснении нефти с помощью ПАВ.
Водный раствор ПАА можно применить для регулирования процесса вытеснения нефти водой, пользуясь его дилатантными свойствами. Для этого закачивают водный раствор ПАА в высокопроницаемые пропластки, снижая этим скорость движения по ним воды. Затем повышают давление нагнетания и увеличивают скорость вытеснения нефти из низкопроницаемых пропластков.
В методе полимерно-мицеллярного заводнения стремятся при использовании небольшого количества углеводорода-растворителя (нефти, спирта, ПАВ) достичь на контакте нефть и комплексный раствор полного смешивания нефти с этим раствором, либо резко снизить на нем поверхностное натяжение (до 10-6 Н/м). При достижении нужного соотношения составляющих раствора образуются физико-химически связанные группы молекул-мицеллы и раствор называют мицеллярным. Важно, что эффективная вязкость мицеллярного раствора больше вязкостей веществ его составляющих. Если вблизи нагнетательных скважин этот раствор переходит в воду, то менее вязкая вода должна будет вытеснять более вязкий мицеллярный раствор при низком коэффициенте вытеснения раствора. Поэтому для продвижения оторочки мицеллярного раствора по пласту используют водный раствор полимера. Такое воздействие на пласт называют мицеллярно-полимерным заводнением.
Вопросы для самоконтроля
1.Почему с увеличением отношения вязкостей нефти и воды нефтеотдача снижается?
2. Запишите формулу закона фильтрации водного раствора ПАА.
3. Что понимают под дилатантными свойствами полимеров?
4. Перечислите критерии применимости полимерного заводнения нефтяных пластов?
5. По какой причине для продвижения оторочки мицеллярного раствора по пласту используют водный раствор полимера?
ЛЕКЦИЯ 8. ВОПРОСЫ ТЕОРИИ ДВИЖЕНИЯ В ПЛАСТЕ ТЕМПЕРАТУРНОГО ФРОНТА ПРИ ВЫТЕСНЕНИЯ НЕФТИ ГОРЯЧЕЙ ВОДОЙ, ПАРОМ
Начальная пластовая температура и ее распределение на месторождении определяются геотермическими условиями. Обычно пластовая температура соответствует среднему геотермическому градиенту в геологическом регионе. Однако наблюдаются и существенные отклонения. Зоны земной коры с высокой температурой называются геотермальными. Температурным режимом месторождения называют распределение пластовой температуры и ее изменение за счет теплопроводности и конвекции.
Изменение содержания тепла в пласте и, следовательно, пластовой температуры происходит в основном при закачке в пласт воды, с иной температурой, чем начальная пластовая, при отборе нефти, а также при экзотермических реакциях в пласте.
Рассмотрим процесс вытеснения нефти водой из однородного прямолинейного пласта при закачивании воды с температурой большей чем пластовая. Для вывода уравнения переноса тепла рассмотрим элемент прямолинейного пласта. Слева в элемент пласта длиной ∆ х, высотой h и шириной b поступает вода с температурой Т. В пласте начинается перенос тепла за счет конвекции и теплопроводности. Если 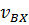 – скорость фильтрации воды в направлении оси х, то скорость ввода тепла в элемент пласта за счет конвекции через его левую грань будет
– скорость фильтрации воды в направлении оси х, то скорость ввода тепла в элемент пласта за счет конвекции через его левую грань будет 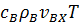 . Через правую грань элемента пласта происходит теплоотдача со скоростью:
. Через правую грань элемента пласта происходит теплоотдача со скоростью:
 (8.1)
(8.1)
где сВ – удельная теплоемкость воды; ρ в – плотность воды.
За счет теплопроводности через левую грань элемент получает тепло со скоростью  и через правую грань он отдает тепло со скоростью
и через правую грань он отдает тепло со скоростью  . В элементе пласта содержатся остаточная нефть и вода. Поэтому приращение теплосодержания в нем выражается так:
. В элементе пласта содержатся остаточная нефть и вода. Поэтому приращение теплосодержания в нем выражается так:
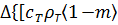 +
+ 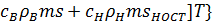 (8.2)
(8.2)
где 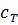 – массовая удельная теплоемкость минералов, слагающих горные породы;
– массовая удельная теплоемкость минералов, слагающих горные породы; 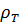 – плотность минералов; s – водонасыщенность.
– плотность минералов; s – водонасыщенность.
Скорость  распространения тепла за счет теплопроводности выражается законом Фурье. Если
распространения тепла за счет теплопроводности выражается законом Фурье. Если  то согласно балансу тепла в элементе пласта получим:
то согласно балансу тепла в элементе пласта получим:
 (8.3)
(8.3)
Здесь 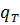 - скорость отдачи тепла с единицы площади кровли и подошвы пласта за счет теплопроводности. Теплоотдача идет через две границы- через кровлю и через подошву пласта, что учитывается множителем 2 в последнем члене правой части формулы.
- скорость отдачи тепла с единицы площади кровли и подошвы пласта за счет теплопроводности. Теплоотдача идет через две границы- через кровлю и через подошву пласта, что учитывается множителем 2 в последнем члене правой части формулы.
Механизм переноса тепла в нефтяном пласте при вытеснении нефти водой имеет важную для разработки нефтяных месторождений особенность. Граница охлаждаемой или нагреваемой водой зон в пористой среде перемещается в пласте значительно медленнее чем движется вода. При закачке в пласт воды с температурой, отличающейся от пластовой, образующаяся при этом в пласте охлажденная или нагретая зона, отстает от фронта вытеснения нефти водой.
Покажем это, решая приведенное выше уравнение. Для простоты пренебрежем переносом тепла за счет теплопроводности вдоль оси х и отдачей тепла в кровлю и подошву.
Выносим за знаки соответствующих производных скорость конвективного переноса тепла 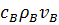 и величину:
и величину:
 (8.4)
(8.4)
учитывая, что  .
.
В результате, исключив из рассматриваемого уравнения взаимно уничтожающиеся члены, и, полагая  , получим уравнение тепло- переноса:
, получим уравнение тепло- переноса:
 5)
5)
В прямолинейный пласт слева через границу х = 0 закачивается холодная вода при постоянном расходе q и температуре Т1 < Тпл (Тпл – начальная пластовая температура).
B пласте образуется фронт охлаждения с координатой  . Темпера- тура в области до координаты
. Темпера- тура в области до координаты  составит
составит 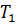 , а перед этой координатой температура равна пластовой Тпл. Фронт охлаждения по мере закачки холодной воды перемещается со скоростью:
, а перед этой координатой температура равна пластовой Тпл. Фронт охлаждения по мере закачки холодной воды перемещается со скоростью:
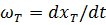 . (8.6)
. (8.6)
Решение уравнения (16.1) ищем в виде:
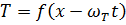 (8.7)
(8.7)
где f – функция от переменной 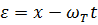 .
.
Имеем:
 ;
;  . (8.8)
. (8.8)
Подставив (16.4) в (16.1), получим:
 . (8.9)
. (8.9)
В общем случае 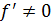 . Откуда следуeт:
. Откуда следуeт:  (8.10)
(8.10)
Оценим величину  при данных, характерных для нефтяных пластов, при
при данных, характерных для нефтяных пластов, при  ;
;  ;
; 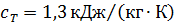 ;
; 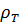 = 2,5
= 2,5 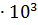 кг/
кг/  ; m=0,2;
; m=0,2;  ;
; 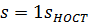 = 0,6;
= 0,6;  =2,1 кДж/(кг
=2,1 кДж/(кг  К);
К); 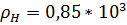 кг/
кг/  ;
;  = 0. Получим:
= 0. Получим:

Следовательно фронт охлаждения в 1,29 раза двигается быстрее чем фильтруется вода в пласте. Если же отнести скорость фронта охлаждения к истинной скорости фронта поршневого вытеснения нефти водой 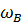 , то получаем:
, то получаем:

Следовательно, фронт охлаждения в каждый момент времени отстает от фронта вытеснения нефти водой в 1/0,155 = 6,45 раза. Это значит, что нефть будет вытесняться из пласта поршневым образом не закачиваемой холодной водой, а водой с пластовой температурой.
Однако рассмотренный пласт однороден, кровля и подошва теплоизолированы. В реальном пласте закачиваемая холодная вода в основном проникает в наиболее высокопроницаемый пропласток. Нефть в нем значительное время вытесняется водой с пластовой температурой. В течении этого времени в нем не ухудшаются условия вытеснения нефти по сравнению с условиями в процессе закачки воды при пластовой температуре. В соседних же менее проницаемых пропластках температура будет уменьшаться (из-за опережающего движения холодной воды в высокопроницаемых прослоях) и ухудшатся условия вытеснения, особенно если нефть резко увеличивает вязкость с понижением температуры или в нефти кристаллизуется парафин и она приобретает неньютоновские свойства.
Заметим, что при закачке горячей воды или пара в соседних менее проницаемых пропластках температура будет повышаться, вязкость нефти снижаться и вытеснение возможно будет происходить при улучшенных условиях.
Во время закачки в пласт воды с температурой большей пластовой образуется тепловая зона. Переднюю границу ее называют фронтом нагрева или тепловым фронтом. Скорость его продвижения можно определить аналогично фронту охлаждения. Но при закачке горячей воды из прогретой зоны 0  (
(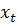 - координата теплового фронта на рисунке 8.1) будет дополнительно вытесняться нефть. В момент времени t распределение насыщенности пласта водой и остаточной нефтью показано на рисунке 8.1. Если моменту t в пласт закачан объем воды, равный
- координата теплового фронта на рисунке 8.1) будет дополнительно вытесняться нефть. В момент времени t распределение насыщенности пласта водой и остаточной нефтью показано на рисунке 8.1. Если моменту t в пласт закачан объем воды, равный 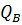 , то его величина определится выражением:
, то его величина определится выражением:
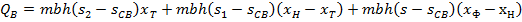
Разделив его левую и правую части на bh, продиффенцировав его по t, раскрыв скобки, получим:
 , (8.11)
, (8.11)
 (8.12)
(8.12)
Рассматривая баланс нефти, вытесненной из зоны 0  в зону
в зону  , имеем:
, имеем:
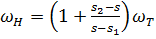 (8.13)
(8.13)
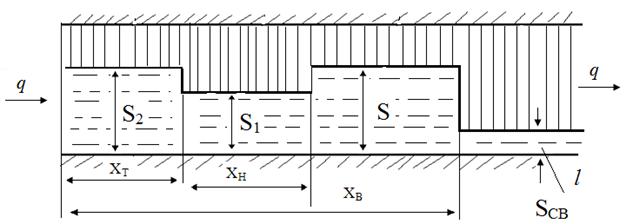
Рисунок 8.1 – Схема вытеснения нефти из прямолинейного пласта горячей водой
Теперь из (8.11)найдем:
 .
.
Таким образом, и в случае вытеснения нефти из пласта горячей водой с температурой t, тепловой фронт отстает от фронта вытеснения нефти. Нефть будет вытесняться сначала водой с пластовой температурой и только в зоне 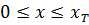 станет вытесняться горячей водой. Дополнительная нефть начнет добываться спустя время, после которого «передняя координата» нефтяного вала
станет вытесняться горячей водой. Дополнительная нефть начнет добываться спустя время, после которого «передняя координата» нефтяного вала  достигнет конца пласта.
достигнет конца пласта.
При расчетах неизотермических процессов разработки нефтяных месторождений используют уравнение теплопереноса, учитывающих отдачу тепла в кровлю и подошву пласта.
1. При оценочных расчетах неизотермических процессов реальных пластов прибегают к способу Ньютона:
qT = 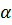 *(T - T пл) (8.14)
*(T - T пл) (8.14)
где 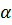 - коэффициент теплопередачи пласта.
- коэффициент теплопередачи пласта.
Однако способ Ньютона более пригоден в лабораторных условиях для физических моделей пластов.
2. Ловерье решал уравнение теплопереноса при следующих упрощениях. Температура пласта в каждом вертикальном сечении или в каждом элементе пласта длиной  принималась одинаковой, пренебрегалось теплопроводностью пласта по горизонтали. Перенос тепла в кровле и подошве за счет теплопроводности принимался происходящим только по вертикали. Условно считалось, что кровля и подошва пласта простираются соответственно вверх и вниз до бесконечности (так как отдача тепла за счет теплопроводности происходит медленно). Не учитывалась слабая зависимость теплоемкости воды и горных пород от температуры.
принималась одинаковой, пренебрегалось теплопроводностью пласта по горизонтали. Перенос тепла в кровле и подошве за счет теплопроводности принимался происходящим только по вертикали. Условно считалось, что кровля и подошва пласта простираются соответственно вверх и вниз до бесконечности (так как отдача тепла за счет теплопроводности происходит медленно). Не учитывалась слабая зависимость теплоемкости воды и горных пород от температуры.
В результате Ловерье записал уравнение теплопереноса в прямолинейном пласте при поршневом вытеснении нефти водой в виде:
 (8.15)
(8.15)
Для расчета движения вала нефти и воды в пласте используем схему распределения нефтеводонасыщенности, приведенную на рисунке 8.1.
При учете ухода тепла по Ньютону в уравнение (8.15) подставим выражение для 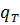 , определяемое формулой (8.14). Ловерье же использовал решение задачи о распространении тепла в прямолинейном стержне. Если, например, кровлю пласта считать сечением соответствующим Z =0, то с элемента пласта длиной
, определяемое формулой (8.14). Ловерье же использовал решение задачи о распространении тепла в прямолинейном стержне. Если, например, кровлю пласта считать сечением соответствующим Z =0, то с элемента пласта длиной  и шириной b при постоянном перепаде температур будет уходить в единицу времени количество тепла, равное:
и шириной b при постоянном перепаде температур будет уходить в единицу времени количество тепла, равное:
 (8.16)
(8.16)
Следовательно:
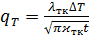 , (8.17)
, (8.17)
где  - коэффициенты теплопроводности и температуропроводности горных пород кровли и подошвы пласта.
- коэффициенты теплопроводности и температуропроводности горных пород кровли и подошвы пласта.
Из (8.11) видно, что скорость отдачи тепла в кровлю и подошву пласта с течением времени t уменьшается.
Формула (8.16) пригодна при 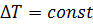 . При переменном перепаде температур следует использовать интеграл Дюамеля.
. При переменном перепаде температур следует использовать интеграл Дюамеля.
Если учитывать непоршневой характер вытеснения нефти водой, то уравнение (8.15) перед производной ∂Т/∂х должно содержать не 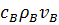 , а член
, а член  Гидродинамическая часть расчета в этом случае основывается, как и при изотермическом вытеснении нефти водой, на использовании относительных проницаемостей для нефти и воды и функции:
Гидродинамическая часть расчета в этом случае основывается, как и при изотермическом вытеснении нефти водой, на использовании относительных проницаемостей для нефти и воды и функции:
 (8.18)
(8.18)
Расчеты непоршневого вытеснения нефти водой в неизотермических условиях производят обычно численными методами на ЭВМ.
Вытеснение нефти из пласта водяным паром может осуществляться вблизи паронагнетательных скважин. При нагнетании насыщенного пара в нефтяной пласт По мере продвижения насыщенного пара в нефтяном пласте его сухость уменьшается.В итоге пар полностью сконденсируется и превратится в горячую воду.
Закономерности премещения области насыщенного пара с постоянной температурой в пласте можно установить по формуле Маркса– Лангенгейма, которая выводится непосредственно на основе баланса тепла в пласте:
 (8.19)
(8.19)
Здесь q – количество тепла, вводимого в пласт в единицу времени с паром;  – изменение за единицу времени тепла в нагретой области;
– изменение за единицу времени тепла в нагретой области; 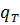 – измене- ние за единицу времени тепла, отдаваемого в кровлю и подошву. В расчетной схеме Маркса-Лангенгейма использована схема теплопотерь Ловерье.
– измене- ние за единицу времени тепла, отдаваемого в кровлю и подошву. В расчетной схеме Маркса-Лангенгейма использована схема теплопотерь Ловерье.
В нагретой области пласта 1, содержащей насыщенный пар и остаточную нефть с насыщенностью 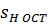 , температура равна температуре
, температура равна температуре  нагнетаемого пара. В области 2, расположенной перед областью 1, температура равна пластовой.
нагнетаемого пара. В области 2, расположенной перед областью 1, температура равна пластовой.
Допустим, что тепловой фронт, продвинувшись в глубь пласта, занял положение x =  в некоторый момент времени
в некоторый момент времени  .Только с этого момента начнется уход тепла в кровлю и подошву по вновь образовавшейся площадке
.Только с этого момента начнется уход тепла в кровлю и подошву по вновь образовавшейся площадке 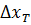 . Отдача тепла из пласта в кровлю и подошву в соответствии с полученной ранее формулой выражается так:
. Отдача тепла из пласта в кровлю и подошву в соответствии с полученной ранее формулой выражается так:

 (8.20)
(8.20)
Для нагретой области 1 имеем:
 ; (8.21)
; (8.21)

Подставляя (8.20) и (8.21) в уравнение баланса тепла (8.15), и, переходя к пределу при  и
и  , получим:
, получим:
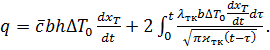 (8.22)
(8.22)
Решение уравнения (8.22) найдено с использованием преобразования Лапласа:

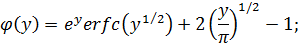
 ;
;  (8.23)
(8.23)
Подставляя время t в последнюю из формул (8.23), находим соответствующее ему значение y, по нему определяем  и затем по первой формуле (8.23) вычисляем координату теплового фронта
и затем по первой формуле (8.23) вычисляем координату теплового фронта  .
.
Скорость теплового фронта  получаем дифференцированием первого выражения:
получаем дифференцированием первого выражения:
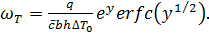 (8.24)
(8.24)
Коэффициент тепловой эффективности процесса определяется выражением:
 . (8.25)
. (8.25)
По графической зависимости  на рисунке 8.2 видно, что с ростом безразмерного времени
на рисунке 8.2 видно, что с ростом безразмерного времени  коэффициент тепловой эффективности процесса
коэффициент тепловой эффективности процесса  уменьшается, поскольку с течением времени все большее количество тепла уходит в кровлю и подошву пласта.
уменьшается, поскольку с течением времени все большее количество тепла уходит в кровлю и подошву пласта.
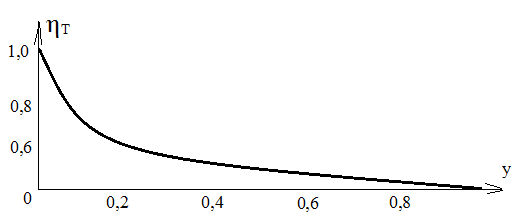
Рисунок 8.2 – Зависимость изменения тепловой эффективности процесса вытеснения нефти паром  от безразмерного времени у
от безразмерного времени у
Рассмотренную схему теплопереноса в пласте при закачке в него пара можно использовать и в случае радиальной фильтрации. При этом вместо первого уравнения выражения (8.23) записываем:
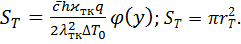 (8.26)
(8.26)
где 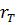 – радиус нагретой области. Функцию
– радиус нагретой области. Функцию  и безразмерное время у определяем по формуле (8.23) как и для прямолинейного пласта. Распределение насыщенностей пласта водой и нефтью при радиальной фильтрации можно установить по модели поршневого вытеснения нефти водой.
и безразмерное время у определяем по формуле (8.23) как и для прямолинейного пласта. Распределение насыщенностей пласта водой и нефтью при радиальной фильтрации можно установить по модели поршневого вытеснения нефти водой.
Вопросы для самоконтроля
1.Почему в случае вытеснения нефти из пласта горячей водой, тепловой фронт отстает от фронта вытеснения нефти?
2. Дайте определения понятиям «насыщенный пар», «сухость пара».
3. Запишите уравнение теплопереноса в прямолинейном пласте при поршневом вытеснении нефти водой; объяснитесхему теплопотерь Ловерье (за счет изменения каких физических величин осуществляется теплоперенос?).
4. От каких параметров зависит коэффициент тепловой эффективности процесса вытеснения нефти горячим паром?
5.От каких параметров зависит скорость отдачи тепла из пласта в его кровлю и подошву?
ЛЕКЦИЯ 9. ВОПРОСЫ ТЕОРИИ ВЫТЕСНЕНИЯ НЕФТИ ИЗ ПЛАСТА ПРИ ПЛАСТОВОМ ГОРЕНИИ
При внутрипластовом горении в пористой среде сгорает в основном тяжелый остаток нефти (кокс). Более легкие фракции нефти испаряются перед областью горения в результате повышения температуры и переносятся в сторону вытеснения к добывающим скважинам.
Начинают работы с возбуждения или инициирования горения в пласте. Для этого в нагнетательную скважину опускают глубинную горелку или электронагреватель и нагнетают воздух. Воздух из-за значительно меньшей вязкости, чем насыщающие пласт нефть и вода, прорывается через них к добывающим скважинам. В результате осуществляется сообщаемость (сбойка) воздухонагнетательных и добывающих скважин. Затем включают глубинное нагревательное устройство и вводят тепло в пласт. Постепенно температура в пласте повышается, скорость окисления нефти возрастает и окисление ее переходит в горение. Окислителем является кислород, находящийся в составе закачиваемого в пласт воздуха. Горение идет в малой зоне пласта (фронте горения шириной в несколько сантиметров). Нефть отбирается скважинами вместе с продуктами горения и водой.
При низкотемпературном окислении (когда давление меньше 5 МПа, а температура находится в пределах 420–450 К) углерод и водород нефти соединяются с кислородом, образуя окислы углеводородов и органические кислоты, а при высокотемпературном горении (когда температура выше 200 оС) образуются в основном углекислый газ и вода.
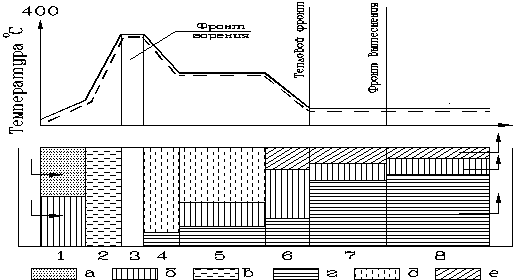
а - воздух; б - вода; в - смесь пара и воздуха; г - нефть; д - смесь пара и газов горения; е - газы горения
Рисунок 9.1 – Схема влажного внутрипластового горения
Скорость горения определяется быстротой подачи воздуха в зону окислительной реакции. Скорость продвижения фронта горения в пласте определяется расходом окислителя q воз (м3/сут) и Rвоз (м3/м3):
ωф = q воз /(Rвоз bh) (9.1)
где q воз - расход воздуха в прямолинейный элемент пласта шириной b и толщиной h, охваченной горением.
Положение фронта горения в момент времени t определяется выражением:
 =
=  . (9.2)
. (9.2)
При плоско-радиальной фильтрации имеем:
 ;
; 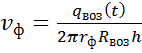 .
.
Отсюда получаем расстояние, на котором находится положение фронта горения в момент времени t:
 . (9.3)
. (9.3)
Если в скважину в радиальном случае нагнетать при стандартных условиях q воз = 30000 м3/сут при h = 10м, Rвоз= 308м3/м3, то через 1 год (365сут) фронт горения продвинется от скважины на расстояние 
Из приведенных формул видно, что при постоянном расходе закачиваемого в пласт воздуха скорость движения фронта горения, тем меньше чем больше кокса содержится в 1м3пласта.
Сухое внутрипластовое горение осуществляется при нагнетании в пласт только воздуха.

Рисунок 9.2 – Кривая изменения температуры при сухом внутрипластовом горении
Наибольшая температура Т* на рисунке 9.2 соответствует положению фронта горения с координатой хф. Излом на линии температуры на расстоянии хТ определяет положение фронта конвекции при конвективном переносе тепла. Скорости перемещения этих фронтов разные потому что они зависят от различных факторов.
При сухом внутрипластовом горении скорость перемещения фронта конвекции в 5–7 раз меньше скорость движения фронта горения. Значит, тепло, генерируемое в зоне горения, мало работает на вытеснение нефти, оно остается позади области горения, бесполезно уходя в кровлю и подошву пласта.
Тепло, генерируемое в зоне горения, станет эффективнее использоваться если оно будет переноситься в область перед фронтом горения. При этом оно будет испарять легкие фракции нефти, которые двинутся к добывающим скважинам, а оставшиеся тяжелые фракции будут сгорать.

Рисунок 9.3 – Схема распределения температуры и насыщенности пористой среды пласта при влажном горении
Такой конвективный перенос тепла возможен при увеличении теплоемкости движущихся в пласте веществ. Что достигается добавлением воды к нагнетаемому в пласт воздуху.
Влажное горение в пласте осуществляется при закачке в него воздуха с водой. При влажном горении в пласте (в некоторых случаях) фронт конвекции примерно в два раза движется быстрее, чем фронт горения.
При интенсивном горении ширина зоны горения с пиковой температурой мала (рисунок 9.3). Перед ней движется паровое плато с постоянной температурой. Она сильно насыщена водяным паром и продуктами горения. В ней в основном и происходит вытеснение нефти. Ее легкие фракции испаряются и вытесняются к добывающим скважинам.
Расчеты процессов горения в пласте сложны и ведутся на мощных вычислительных машинах. Существуют и приближенные способы расчетов.
Вопросы для самоконтроля
1. От чего зависит скорость процесса внутрипластового горения?
2. Раскройте содержание понятий: «конвекция», «теплоперенос»?
3. Почему п ри сухом внутрипластовом горении скорость перемещения фронта конвекции значительно меньше скорости движения фронта горения?
4. Назовите преимущества влажного пластового горения?
5. Изобразите схему внутрипластового горения. Назовите зоны которые образуются при внутрипластовом горении? Укажите какие физические процессы происходят в каждой из зон?
НАИМЕНОВАНИЕ И СОДЕРЖАНИЕ ПРАКТИЧЕСКИХ ЗАНЯТИЙ. ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ






