Кинематическое исследование механизма осуществляется для каждой структурной группы в порядке их присоединения.
Скорости точек механизма определяется графоаналитическим способом для каждого плана положения в зависимости от угла поворота кривошипа. Метод состоит в графическом решении векторных уравнений.
Сначала определяются скорости точек ведущего механизма. Если ведущее звено совершает вращательное движение, то скорость точки А (Рисунки 5, 6, 7) по величине определяется из выражения
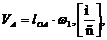
где  -угловая скорость вращения кривошипа.
-угловая скорость вращения кривошипа.
Из полюса Р плана скоростей в направлении вращения кривошипа перпендикулярно к OA откладываем вектор скорости точки A  , где pa - отрезок в мм (обычно длину отрезка выбирают в пределах 60-100 мм), затем определяется масштаб плана скоростей
, где pa - отрезок в мм (обычно длину отрезка выбирают в пределах 60-100 мм), затем определяется масштаб плана скоростей 

Рисунок 5 - Шарнирный четырехзвенник
Построение остальных точек плана зависит от схемы механизма, в частности от присоединённых двухповодковых групп, которые можно разделить на три типа: с вращательными кинематическими парами, с вращательно-поступательными парами и с поступательньно-вращательными парами.
Сначала рассматривается двухповодковая группа, присоединённая к начальному звену, т.е. группа, которой принадлежит шарнир А. Затем определяются точки второй двухповодковой группы, присоединённой к первой и так далее до последней группы.
3.2.2.1. План скоростей двухповодковой группы с вращательными парами.
Построение плана скоростей рассмотрим на примере шарнирного четырёхзвенника О1АВО2 (Рисунок 5).
К кривошипу 1 присоединена группа звеньев 2-3, состоящая из шатуна 2, совершающего плоское движение, и коромысла 3, совершающего вращательное движение. План скоростей точки А уже построен. Вектор 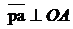 и направлен в сторону вращения ω1.
и направлен в сторону вращения ω1.
Для определения скорости точки В составляем векторное уравнение

в котором двумя чертами подчеркнут вектор известный по величине и направлению, а два других вектора подчеркнуты одной чертой — они известны лишь по направлению.
Строим треугольник скоростей точки В, для чего из полюса плана скоростей Р проводим перпендикуляр к звену 3, а из точки а – перпендикуляр к звену 2. Точка пересечения перпендикуляров определяет положение точки b на плане скоростей, а вектор  изображает вектор скорости
изображает вектор скорости  точки В. Скорости других точек шатуна и коромысла определятся из подобия треугольников или пропорций отрезков. Так положение точки С на плане скоростей определяется пресечением перпендикуляров проведённых из точки а к звену АС, а из точки b к звену ВС. Вектор
точки В. Скорости других точек шатуна и коромысла определятся из подобия треугольников или пропорций отрезков. Так положение точки С на плане скоростей определяется пресечением перпендикуляров проведённых из точки а к звену АС, а из точки b к звену ВС. Вектор  изображает вектор скорости V с точки С. Положения точек S2, S3 и d определяются отрезками
изображает вектор скорости V с точки С. Положения точек S2, S3 и d определяются отрезками 
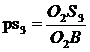 и
и  ; откладываем эти отрезки на плане скоростей. Соединяем полученные точки S2, S3 и d с полюсом плана скоростей Р. Векторы
; откладываем эти отрезки на плане скоростей. Соединяем полученные точки S2, S3 и d с полюсом плана скоростей Р. Векторы  ,
,  ,
,  изображают вектора скоростей точек S2, S3 и d.
изображают вектора скоростей точек S2, S3 и d.
Значения линейных скоростей всех точек определяются выражениями: 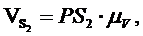


Значения окружных скоростей точек определяются аналогично 
Величины угловых скоростей шатуна и коромысла определяются на основе построения плана скоростей


Для определения направления угловой скорости ω2 следует мысленно перенести вектор  в точку В (первая по записи точка) плана положения механизма и посмотреть куда поворачивается звено относительно точки А (вторая по записи точка). В эту сторону будет направлена угловая скорость.
в точку В (первая по записи точка) плана положения механизма и посмотреть куда поворачивается звено относительно точки А (вторая по записи точка). В эту сторону будет направлена угловая скорость.
Аналогично определяется направление угловой скорости ω3.
3.2.2.2. План скоростей двухповодковой группы с вращательно-поступательными парами.
Построение плана скоростей рассмотрим на примере кривошипно-ползунного механизма (рис.6.)
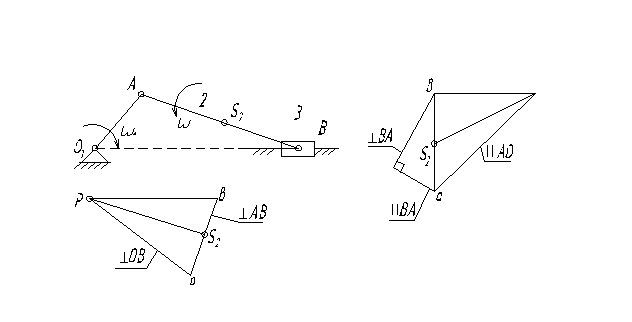
Рисунок 6 -Кривошипно-ползунный механизм
К кривошипу 1 присоединена группа звеньев 2-3, состоящая из шатуна 2, совершающего плоское движение, и ползуна 3, совершающего поступательное движение.
Из произвольной точки Р (полюса плана скоростей) в направлении вращения кривошипа перпендикулярно к OA откладываем вектор скорости точки А  , где
, где 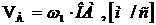 ;
;  ;
; 
Определяем масштаб плана скоростей 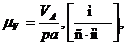
Составляем векторное уравнение скорости точки В

Строим треугольник скоростей точки В в соответствии с уравнением, для чего из точки а проводим прямую, перпендикулярную к звену 2 (линия вектора  ), а через полюс Р проводим прямую параллельную ОВ (линия* вектора
), а через полюс Р проводим прямую параллельную ОВ (линия* вектора  ). Пересечение этих двух прямых определяет точку b, которая является концом вектора
). Пересечение этих двух прямых определяет точку b, которая является концом вектора  , изображающего на плане вектор скорости точки В. Положение других точек шатуна на плане скоростей определяется из подобия треугольников, либо из пропорции отрезков, так
, изображающего на плане вектор скорости точки В. Положение других точек шатуна на плане скоростей определяется из подобия треугольников, либо из пропорции отрезков, так 
Откладываем отрезок 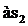 на плане, соединяем точку S2 с полюсом Р плана и получаем вектор
на плане, соединяем точку S2 с полюсом Р плана и получаем вектор  . Значения линейных скоростей точек определяются произведением длин отрезков на масштаб плана скоростей.
. Значения линейных скоростей точек определяются произведением длин отрезков на масштаб плана скоростей.
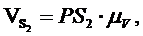


Угловая скорость вращения шатуна по величине будет равна 
Направление ω2 определяется переносом вектора  в точку В плана положения механизма и вращением звена относительно точки А под действием этого вектора.
в точку В плана положения механизма и вращением звена относительно точки А под действием этого вектора.
3.2.2.3. План скоростей двухповодковой группы с поступательно-вращательными кинематическими парами.
Под этой группой понимают такое соединение звеньев при котором поступательная кинематическая пара находится в плоскопараллельном движении. Построение плана скоростей рассмотрим на примере кулисного механизма (Рисунок 7).

Рисунок 7
К кривошипу 1 присоединена группа звеньев 2-3, состоящая из камня кулисы 2 и кулисы 3, совершающей вращательное движение вокруг точки O2.
Из полюса Р плана скоростей в направлении вращения кривошипа, перпендикулярно к O1A откладываем вектор абсолютной скорости точки А1 кривошипа 



Определяем масштаб плана скоростей 
Скорости точки А2 камня кулисы равна скорости точки A1  и равна геометрической сумме скоростей точки в переносном движении
и равна геометрической сумме скоростей точки в переносном движении  и скорости точки в относительном движении
и скорости точки в относительном движении  ,
,  , т.е.
, т.е.

Строим треугольник скоростей в соответствии с уравнением, для чего из начала вектора  проводим перпендикуляр к кулисе 02А, а из конца вектора
проводим перпендикуляр к кулисе 02А, а из конца вектора  проводим линию, параллельную кулисе 02А до взаимного пересечения. Получаем точку а3. Векторы
проводим линию, параллельную кулисе 02А до взаимного пересечения. Получаем точку а3. Векторы  и
и 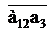 являются векторами переносной
являются векторами переносной  и относительной
и относительной  скоростей точки А соответственно.
скоростей точки А соответственно.
Величины этих скоростей будут равны 

Величина угловой скорости кулисы  Направление ω3 определяется направлением вращения кулисы под действием вектора
Направление ω3 определяется направлением вращения кулисы под действием вектора  .
.
3.3.3. Определение ускорений точек и угловых ускорений звеньев механизма.
Определение линейных ускорений точек звеньев происходит в той же последовательности, что и определение скоростей. Ускорения точек определяются путём построения планов ускорений для каждого положения механизма.
Сначала определяются ускорения точек ведущего звена. Если ведущее звено совершает равномерное вращательное движение, то ускорение наиболее удалённой точки А равно нормальному ускорению  и направлено по радиусу вращения к центру вращения (Рисунки 5 - 7).
и направлено по радиусу вращения к центру вращения (Рисунки 5 - 7).
Из полюса плана ускорений - π откладываем вектор 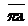 параллельно звену O1A в направлении от точки А и точке 01 в соответствии со схемой механизма. Длина этого вектора изображает на плане ускорений вектор ускорения точки A
параллельно звену O1A в направлении от точки А и точке 01 в соответствии со схемой механизма. Длина этого вектора изображает на плане ускорений вектор ускорения точки A  и выбирается произвольно, исходя из удобства размещения на чертеже. (Обычно ра = 60 -120мм)
и выбирается произвольно, исходя из удобства размещения на чертеже. (Обычно ра = 60 -120мм)
Определяем масштаб плана ускорений μ W

Ускорения остальных точек плана ускорений механизма зависит от присоединённых групп Ассура.
3.3.3.1. План ускорений двухповодковой группы с вращательными парами.
Построение плана ускорений рассмотрим на примере шарнирного черырехзвенника О1АВО2 (Рисунок 5).
Ускорение точки В складывается из ускорения точки А и относительного ускорения точки В при вращении звена 2 вокруг точки А. С другой стороны точка В принадлежит звену 3 и движется по окружности вокруг точки О2. Таким образом, имеем систему двух векторных уравнений

Нормальные составляющие ускорений равны по величине.
 и
и  ,
,
где а b и pb - отрезки, взятые из плана скоростей.
Нормальное ускорение 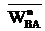 направлено вдоль звена АВ от точки В к точке А, а нормальное ускорение
направлено вдоль звена АВ от точки В к точке А, а нормальное ускорение  - вдоль звена ВО2 от точки В к точке О2.
- вдоль звена ВО2 от точки В к точке О2.
Тангенциальные составляющие ускорений  и
и  по величине неизвестны, известны по направлению:
по величине неизвестны, известны по направлению:  ;
; 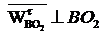
Решаем совместно систему уравнений графически. Из конца вектора  (точки а) откладываем вектор
(точки а) откладываем вектор  || АВ, направленный от точки В к точке А, величина которого равна
|| АВ, направленный от точки В к точке А, величина которого равна 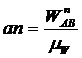 , а из полюса π откладываем вектор
, а из полюса π откладываем вектор  || ВО2 направленный от точки В к точке О2, величина которого равна
|| ВО2 направленный от точки В к точке О2, величина которого равна  . Затем из точки n проводим линию действия вектора
. Затем из точки n проводим линию действия вектора  , которая
, которая  АВ, а из точки n1 — линию действия вектора
АВ, а из точки n1 — линию действия вектора  , которая
, которая 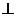 ВO2. На пересечении линий получаем точку b. Соединив точку b с полюсом π, получаем вектор ускорения точки В
ВO2. На пересечении линий получаем точку b. Соединив точку b с полюсом π, получаем вектор ускорения точки В 
Ускорение других точек шатуна и коромысла определяются из подобия треугольников или пропорций отрезков.
Для определения положения точки С на плане ускорений строим треугольник abc, подобный треугольнику ABC на плане положений механизма, для чего отрезок ab на плане ускорений поворачиваем вокруг точки а на угол α, а вокруг точки b на угол β, сохраняя правило обхода контура до пересечения повернутых отрезков.
Положение точек S2, S3 и d определяются отрезками 
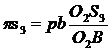 и
и 
Откладываем эти отрезки на плане ускорений. Соединим полученньи точки S2, S3, d с полюсом плана ускорений π. Векторы  ,
,  ,
,  изображают векторы ускорений точек S2, S3, d.
изображают векторы ускорений точек S2, S3, d.
Значения ускорений всех точек определяются выражениями:






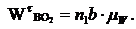
Значения угловых ускорений шатуна 2 и коромысла 3 определяются следующими выражениями:


Направление углового ускорения ε2 определяется направлением вращения звена 2 вокруг точки А под действием вектора касательного ускорения  , приложенного в точке В плана положения механизма. Для данного положения ускорение ε2 направлено по часовой стрелке.
, приложенного в точке В плана положения механизма. Для данного положения ускорение ε2 направлено по часовой стрелке.
Аналогично определяется направление ускорения ε3.
3.3.3.2. План ускорений двухповодковой группы с вращательно-поступательными кинематическими парами.
Построение плана ускорений рассмотрим на примере кривошипно-ползунного механизма (рис. 6).
Из полюса плана ускорений πоткладываем вектор  ускорения точки А кривошипа.
ускорения точки А кривошипа.
Ускорение точки В находим по уравнению

Нормальное ускорение точки В вокруг точки А  величине равна
величине равна  . Из конца вектора ускорения точки А
. Из конца вектора ускорения точки А  откладываем вектор
откладываем вектор  || ВА, направленный от точки В к точке А, величина которого равна
|| ВА, направленный от точки В к точке А, величина которого равна 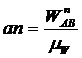 . Затем из точки n проводим линию действия касательного ускорения
. Затем из точки n проводим линию действия касательного ускорения  , которая
, которая  АВ, а из полюса плана ускорений πпроводим линию || ускорению
АВ, а из полюса плана ускорений πпроводим линию || ускорению  (горизонтальная линия). На пересечении линий получаем точку b. Получаем вектор ускорений точки В -
(горизонтальная линия). На пересечении линий получаем точку b. Получаем вектор ускорений точки В -  .
.
Ускорения любой точки шатуна определяются аналогично определению скоростей точек на плане скоростей.
Угловое ускорение шатуна ε2 определяется аналогично тому, как это было сделано ранее.
3.3.3.3. План ускорений двухповодковой группы с поступательно-вращательными кинематическими парами.
Построение плана ускорений рассмотрим на примере кулисного механизма (Рисунок 7).
Первой точкой ускорение которой следует определить, является точка А1 ведущего звена (кривошипа OA). Из полюса плана ускорений πоткладываем вектор параллельно звену AO1 в направлении от точки А к точке О.
Следующая точка А2, принадлежащая камню кулисы. Ускорения точек А1 и А2 будут равны (шарнирное соединение), т.е.  .
.
Точка А2 совершает сложное движение её ускорение складывается из ускорений точки A3 (переносное движение точки) и ускорения точки А2 при движении звена 2 по звену 3 (относительное движение точки), т.е.

Поскольку траекторией движения точки Аз является окружность, то переносное ускорение точки A3 состоит из двух частей  , где
, где 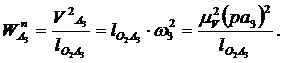
Поскольку звено 3 совершает вращение вокруг неподвижной оси, то относительное ускорение точки состоит из двух частей: 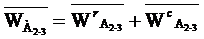 , где
, где  - Кориолисово ускорение точки. Величина ускорения Кориолиса равна
- Кориолисово ускорение точки. Величина ускорения Кориолиса равна 
Для определения направления ускорения Кориолиса следует вектор относительной скорости  повернуть на 90° в сторону вращения, обусловленного угловой скоростью ω3. Итак:
повернуть на 90° в сторону вращения, обусловленного угловой скоростью ω3. Итак:

Строим план ускорений точки А2 согласно уравнению.
Из полюса плана скоростей π откладываем вектор  || О2А,направленный от точки А к точке О2, размер которого определяется
|| О2А,направленный от точки А к точке О2, размер которого определяется  , а из точки n проводим линию действия вектора
, а из точки n проводим линию действия вектора 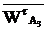 , которая
, которая 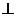 O2А. Далее из конца вектора
O2А. Далее из конца вектора  (точки a 12) откладываем вектор
(точки a 12) откладываем вектор 
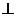 O 2 А, направленный к точке a (вектор
O 2 А, направленный к точке a (вектор  должен подходить к точке a), размер которого определяется
должен подходить к точке a), размер которого определяется 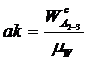 . Затем из точки К проводим линию действия вектора
. Затем из точки К проводим линию действия вектора  , которая || O2А. На пересечении линий получаем точку a 3 Соединяя точки πи a 3, получим ускорение точки
, которая || O2А. На пересечении линий получаем точку a 3 Соединяя точки πи a 3, получим ускорение точки  . Значения ускорений определяется из выражений:
. Значения ускорений определяется из выражений:

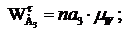

Величина углового ускорения ε3 определяется по выражению:

Направление ε3 определяется направлением вращения звена 3 вокруг точки О2 под действием вектора ускорения 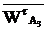 приложенного в точке А плана положения механизма. Для данного положения механизма ускорение ε3 направлено против часовой стрелки.
приложенного в точке А плана положения механизма. Для данного положения механизма ускорение ε3 направлено против часовой стрелки.
3.3.3.4. Графическое определение длин отрезков нормального и Кориолисова ускорений на плане ускорений.
Нормальное и Кориолисово ускорения можно определить путём вычисления по формулам. Однако для построения плана ускорений важно знать не сами ускорения, а длину выражающих их отрезков. Например, длина вектора, выражающего в масштабе  нормальное ускорение точки А равна
нормальное ускорение точки А равна
 или
или 
где (ab) - отрезок на плане скоростей; AB - отрезок на плане положений.
Величина  повторяется при вычислении каждого нового ускорения и её можно вычислить заранее. Целесообразно выбирать
повторяется при вычислении каждого нового ускорения и её можно вычислить заранее. Целесообразно выбирать  так, чтобы указанная величина была равна некоторому круглому числу или ещё лучше, единице.
так, чтобы указанная величина была равна некоторому круглому числу или ещё лучше, единице.
Тогда  и вычисления значительно упрощаются.
и вычисления значительно упрощаются.

Более наглядны и практически безошибочны графические способы вычисления, в качестве примера на рисунке 8а построен отрезок n.

Рисунок 8 - Вычисление ускорений
Берётся произвольный угол, на одной её стороне откладывается отрезок АВ, снятый из плана положений, и на обеих сторонах отрезок ab = ab, снятый с плана скоростей. Точка В и b соединяются прямой линией, а через b проводится прямая, || Вb до пересечения с прямой ab в точке X. Отрезок ах и является искомым.
На рисунке 8б представлено аналогичное построение отрезка С  ;
;  выражающего Кориолисово ускорение
выражающего Кориолисово ускорение  масштабе
масштабе  . Отрезки ра3 и а a 3 снимаются с плана скоростей, отрезок ОгА с плана положений. Построение нормальных и Кориолисовых ускорений выполняются на листе и снабжаются соответствующими заголовками.
. Отрезки ра3 и а a 3 снимаются с плана скоростей, отрезок ОгА с плана положений. Построение нормальных и Кориолисовых ускорений выполняются на листе и снабжаются соответствующими заголовками.
3.4 Кинетостатический расчет механизма
Расчет производится для 2 положений механизма в следующей последовательности:
Задачей силового анализа является:
1) Определение сил инерции звеньев.
2) Определение давлений в кинематических парах.
3) Определение уравновешивающей силы на ведущем звене. Известными являются геометрические размеры звеньев, закон движения ведущего звена, внешние силы и моменты.
Силовой анализ механизмов имеет важное значение, так как по найденным давлениям в кинематических парах подбираются подшипники, производится расчет на прочность и жесткость звеньев механизмов, элементов кинематических пар и т.д.
Силовые исследования выполняются в следующем порядке:
1) Структурным анализом определяют номер семейства кинематической цепи, степень подвижности, класс и порядок механизма.
2) Кинематическим анализом определяют скорости и ускорения точек и звеньев механизма.
3) Собственно силовой анализ начинают с последней группы Ассура. При силовом исследовании механизма используется принцип Даламбера, согласно которому звено или группа звеньев механизма рассматриваются в состоянии равновесия, если к внешним силам и моментам, действующим на них, добавить силы и моменты сил инерции. Уравнения равновесия в этом случае называют уравнениями кинетостатики.
Решая задачу силового анализа механизма в курсовом проекте (работе), рекомендуется, сделав следующие допущения: силы трения в кинематических парах малы, ими следует пренебречь; ведущее звено исполнительного механизма (кривошип) вращается с постоянной угловой скоростью (ω1= const); звенья механизма имеют плоскость симметрии параллельную плоскости их движения, определить:
1) силы полезного сопротивления для всех положений;
2) давление во всех кинематических парах в указанных положениях механизма;
3) уравновешивающий момент в указанных положениях механизма двумя методами (методом плана сил и методом Н. Е. Жуковского: полученные результаты сравнить (расхождение вычисленных уравновешивающих моментов должно быть в пределах 5 %).
3.4.1. Внешние нагрузки, действующие на звенья механизма
Основными силами являются движущие силы, совершающие положительную работу и силы полезного сопротивления, возникающие в процессе выполнения работы и совершающие отрицательную работу.
К движущим силам F д относятся: сила давления рабочей смеси на
поршень цилиндра двигателя; момент, развиваемый электродвигателем на выходном валу насоса или компрессора и т.д.
Силами полезного сопротивления Fc является: силы сопротивления резанию в токарном или строгальном станках, силы сопротивления сжимаемого воздуха и т.д.
Внешние силы могут быть постоянными по величине, такие как, например силы тяжести, силы сопротивления резанию металла при постоянном сечении снимаемой стружки. Они могут зависеть от положения звена, на которое они действуют (силы давления газов, действующие на поршень двигателя внутреннего сгорания или компрессора); от скорости (момент электродвигателя); от времени и т.д.
Значения внешних воздействующих должны быть заданы соответствующими механическими характеристиками. Механические характеристики представляют собой аналитические или графические зависимости внешних сил (моментов) от кинематических параметров (обобщенной координаты, обобщенной скорости, времени). Имея характеристику механизма, можно определить силы механизируемого процесса, приложенные к выходному звену или силы движущие, приложенные к входному звену. Например, если представлена индикаторная диаграмма изменения давления газов 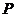 в цилиндре двигателя (компрессора), то силу можно рассчитать по формуле:
в цилиндре двигателя (компрессора), то силу можно рассчитать по формуле:  где
где 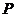 - давление приходящееся на 1 мм2 площади поршня.
- давление приходящееся на 1 мм2 площади поршня.
Силы тяжести звеньев механизма прикладываются в центрах тяжести звеньев и по величине равны 
 где - ускорение свободного падения;
где - ускорение свободного падения;  - масса
- масса 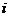 - го звена.
- го звена.
3.4.2. Силы инерции звеньев плоских механизмов
1) Звено совершает поступательное движение (Рисунок 9а). Силы инерции точек звена заменяются главным вектором сил инерции  , приложенным в центре тяжести звена, равным по величине произведению массы звена
, приложенным в центре тяжести звена, равным по величине произведению массы звена  на ускорение центра масс звена
на ускорение центра масс звена  и направленным в сторону, противоположную ускорению центра масс
и направленным в сторону, противоположную ускорению центра масс  . Равнодействующая сил инерции звена
. Равнодействующая сил инерции звена  совпадает в этом случае с главным вектором сил инерции
совпадает в этом случае с главным вектором сил инерции  ;
;
2) Звено совершает вращение вокруг оси с постоянной угловой
скоростью  (Рисунок 9б). Главный вектор сил инерции
(Рисунок 9б). Главный вектор сил инерции  приложен в центре масс
приложен в центре масс  звена, направлен по радиусу кривизны ОА от центра кривизны О и равен
звена, направлен по радиусу кривизны ОА от центра кривизны О и равен  . Равнодействующая сил инерции равна главному вектору сил инерции, т.е.
. Равнодействующая сил инерции равна главному вектору сил инерции, т.е.  ;
;
3) Звено вращается с переменой угловой скоростью  (Рисунок 9в). В этом случае силы инерции точек звена проводятся к главному вектору сил инерции
(Рисунок 9в). В этом случае силы инерции точек звена проводятся к главному вектору сил инерции 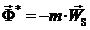 , приложенному в центре масс и к главному моменту сил инерции
, приложенному в центре масс и к главному моменту сил инерции 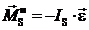 , направленному против углового ускорения звена
, направленному против углового ускорения звена  , где
, где  - момент инерции звена относительно оси, проходящей через центр масс. Главный вектор сил инерции
- момент инерции звена относительно оси, проходящей через центр масс. Главный вектор сил инерции  и главный момент сил инерции
и главный момент сил инерции  могут быть заменены равнодействующей сил инерции
могут быть заменены равнодействующей сил инерции  , векторно-равной главному вектору (
, векторно-равной главному вектору ( ) и приложенной в центре качания звена
) и приложенной в центре качания звена  ,
,  положение которого определяется зависимостями: или
положение которого определяется зависимостями: или
 ;
;
4) Звено совершает плоскопараллельное движение (Рисунок 9г). Силы инерции точек звена проводятся к главному вектору сил инерции,
приложенному в центре масс 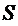 звена и к главному моменту сил инерции относительно центра масс:
звена и к главному моменту сил инерции относительно центра масс:  ;
; 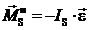 . Главный вектор сил инерции и главный момент сил инерции могут быть заменены равнодействующей сил инерции
. Главный вектор сил инерции и главный момент сил инерции могут быть заменены равнодействующей сил инерции 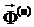 , векторно равной главному вектору (
, векторно равной главному вектору ( )и приложенной в центре инерции, положение которого видно из
)и приложенной в центре инерции, положение которого видно из
построения (Рисунок 9г). Линия  параллельна ускорению полюса
параллельна ускорению полюса  . Линия КТ параллельна относительному ускорению
. Линия КТ параллельна относительному ускорению  .
.

Рисунок 9 – Определение сил инерции звеньев
3.4.3. Последовательность силового анализа механизмов по способу планов сил
Силовой расчет целесообразно проводить в следующей последовательности:
1) Вычертить кинематическую схему механизма в выбранном масштабе и в заданном или указанном преподавателем расчетном положении (желательно в пределах рабочего хода).
2) Определить все внешние силы, приложенные к звеньям механизма: изобразить характеристику рассматриваемой машины (индикаторная диаграмма, график зависимости силы полезного сопротивления от положения ползуна), определить силу полезного сопротивления для всех положений (в пояснительной записке составить таблицу этих сил)
3) Построить или перенести с первого листа курсового проекта план ускорений для рассматриваемого положения механизма, указать на схеме направления угловых ускорений и вычислить силы и моменты сил инерции.
4) Приложить в виде стрелок без масштаба в соответствующие точки кинематической схемы силу полезного сопротивления, силы тяжести, силы и момента сил инерции. К входному звену (кривошипу) приложить уравновешивающий момент при приводе механизма от электродвигателя, направив его по движению звена, или уравновешивающую силу  , чтобы был обеспечен заданный закон движения ведущего звена.
, чтобы был обеспечен заданный закон движения ведущего звена.
5) Произвести расчленение кинематической схемы механизма на группы Ассура и группу начальных звеньев, изобразить каждую группу отдельно и нанести все приложенные силы и моменты, заменив действие «отброшенных» звеньев реакциями, приложенными к элементам кинематических пар.
6) Произвести силовой расчет каждой группы Ассура в отдельности, так как группа Ассура являются статически определимой системой. Расчет следует начинать с группы Ассура присоединенной к механизму при его образовании в последнюю очередь; затем перейти к следующей группе и так до тех пор, пока не будет произведен силовой расчет всех групп, образовавших ведомую часть механизма.
7) В заключение производится силовой расчет ведущего звена, в результате которого определяется идеальный уравновешивающий момент и также нормальная реакция со стороны стойки на кривошип.
3.4.4. Определение уравновешивающего момента (силы) методом «рычага» Н. Е. Жуковского
При решении задач (например, определения мощности двигателя) часто бывает необходимо определить только уравновешивающий момент (силу). Для решения этой задачи удобно применять метод Н. Е. Жуковского.
Н.Е. Жуковский сформулировал теорему, которая гласит: если силу, приложенную к какой либо точке звена плоского механизма, перенести параллельно себе в одноименную точку повернутого на 90° плана скоростей, то момент этой силы относительно полюса плана скоростей будет пропорционален ее мощности.
Согласно общего уравнения динамики системы (принципа Даламбера-Лагранжа) чтобы механическая система, на которую изложены совершенные, голономные, удерживающие связи, находилась в равновесии необходимо и достаточно, чтобы сумма элементарных работ (мощностей) всех заданных сил и сил инерции на возможном перемещение системы равнялась нулю, т.е  или
или 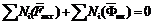 . Согласно теореме Н.Е. Жуковского общее уравнение динамики системы равносильно уравнению моментов всех активных сил и сил инерции относительно полюса повернутого на 90° плана скоростей, т.е
. Согласно теореме Н.Е. Жуковского общее уравнение динамики системы равносильно уравнению моментов всех активных сил и сил инерции относительно полюса повернутого на 90° плана скоростей, т.е  .
.
Для определения уравновешивающей силы на план скоростей в соответствующие точки прикладываем повернутые на 90° в одну сторону внешние силы и силы инерции. Уравновешивающую силу  прикладываем в точке a перпендикулярно вектору
прикладываем в точке a перпендикулярно вектору 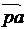 .
.
Составляем уравнение моментов всех сил относительно полюса плана скоростей предварительно измерив плечи сил. Из полученного уравнения определяем  . Если в результате вычислений получается знак минус, то направление уравновешивающей силы следует поменять на противоположное.
. Если в результате вычислений получается знак минус, то направление уравновешивающей силы следует поменять на противоположное.
Уравновешивающий момент определяем по выражению: 
3.4.5. Пример кинетостатического анализа механизма
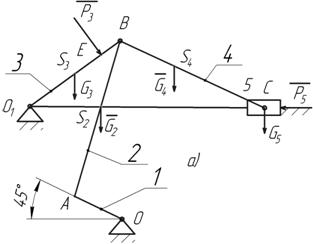

Рисунок 10 - Схема нагружения механизма (а), план ускорений (б)
3.4.5.1. Силы, действующие на звенья механизма
1) Движущая сила Р5;
2) Сила полезного сопротивления Р3;
3) Силы тяжести звеньев 
4) Силы инерции звеньев 
5) Моменты сил инерции звеньев относительно центра масс:

Моменты сил инерции звеньев направлены против направления
угловых ускорений соответствующих звеньев.
Систему, состоящую из силы и пары сил инерции приводим к одной
силе инерции (равнодействующей), равной по величине и направлению той же силе  , но линия действия которой будет смещена от центра тяжести S на расстояние
, но линия действия которой будет смещена от центра тяжести S на расстояние 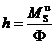 . Направление линии действия равнодействующей относительно центра тяжести S имеет одно и то же направление с инерционным моментом
. Направление линии действия равнодействующей относительно центра тяжести S имеет одно и то же направление с инерционным моментом  .
.
Звено 3 совершает вращательное движение вокруг точки O 1. Сила инерции  звена 3 проходит через центр качания К 3, положение которого определяется по формуле:
звена 3 проходит через центр качания К 3, положение которого определяется по формуле:

Звенья 2 и 4 совершают плоское движение. Равнодействующие сил инерции  и
и  прикладываем в центре инерции Т 2 и Т 4: положения центров качания определяются расстояниями S 2 K 2и S 4 K 4:
прикладываем в центре инерции Т 2 и Т 4: положения центров качания определяются расстояниями S 2 K 2и S 4 K 4:

3.4.5.2. Определение давлений в кинематических парах
Силовой расчет начинаем с последней в порядке присоединения группы Ассура, состоящей из звена 4 и 5, затем группы звеньев 2,3 и заканчиваем силовым расчетом ведущего звена 1.
3.4.5.2.1. Силовой расчет группы Ассура с вращательно-поступательными кинематическими парами (Рисунок 11)
Определяем все внешние силы, действующие на звенья группы 4,5. К звену 5 приложены:  - сила полезного сопротивления;
- сила полезного сопротивления; 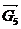 - силы тяжести звена;
- силы тяжести звена; 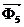 - сила инерции звена; нормальная реакция
- сила инерции звена; нормальная реакция  со стороны стойки на ползун. К звену 4 приложены:
со стороны стойки на ползун. К звену 4 приложены:  - силы тяжести звена;
- силы тяжести звена;  - сила инерции звена, приложенная в центре инерции Т 4 звена. Реакцию со стороны третьего звена на четвертое
- сила инерции звена, приложенная в центре инерции Т 4 звена. Реакцию со стороны третьего звена на четвертое  разложим на две взаимно перпендикулярные составляющие: горизонтальную -
разложим на две взаимно перпендикулярные составляющие: горизонтальную -  и вертикальную -
и вертикальную -  .
.
На группу действует плоская произвольная система сил. Три неизвестные  ,
,  ,
,  определим, составив уравнение равновесия плоской произвольной системы сил. Составим уравнение моментов всех сил относительно точки В.
определим, составив уравнение равновесия плоской произвольной системы сил. Составим уравнение моментов всех сил относительно точки В.

 .
.
Давления  и
и  найдем, построив план сил согласно векторному уравнению равновесия:
найдем, построив план сил согласно векторному уравнению равновесия:
 в масштабе
в масштабе  , откладывая векторы сил в порядке, указанном в уравнении. Векторы, подчеркнутые двумя чертами, известны по величине и направлению, одной чертой – известны по направлению.
, откладывая векторы сил в порядке, указанном в уравнении. Векторы, подчеркнутые двумя чертами, известны по величине и направлению, одной чертой – известны по направлению.
Начинаем построения многоугольника сил из произвольной точки О чертежа, откладывая  , заканчиваем вектором
, заканчиваем вектором  . Затем из начала вектора
. Затем из начала вектора  проводим линию, параллельную
проводим линию, параллельную  , т. е. вертикальную линию, а из конца вектора
, т. е. вертикальную линию, а из конца вектора  линию, параллельную
линию, параллельную  , т. е. горизонтальную линию до пересечения. Получаем замкнутый многоугольник сил, из которого определяем истинные направления реакций
, т. е. горизонтальную линию до пересечения. Получаем замкнутый многоугольник сил, из которого определяем истинные направления реакций  ,
,  ,
,  и их величину, замеряя длины полученных отрезков и умножая их на масштаб плана сил:
и их величину, замеряя длины полученных отрезков и умножая их на масштаб плана сил:
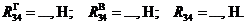
Для более точного определения неизвестных сил составляем аналитические уравнения равновесия в соответствии с условиями равновесия: 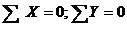 .
.
Давление в кинематическое паре 4-5  определяем из условия равновесия ползуна 5:
определяем из условия равновесия ползуна 5:  . Для чего на плане сил соединяем начало вектора
. Для чего на плане сил соединяем начало вектора 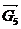 с концом вектора
с концом вектора 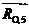


Рисунок 11 – Расчетная схема нагружения и план сил группы звеньев 4,5.
3.4.5.2.2. Силовой расчет группы Ассура с вращательными кинематическими парами

Рисунок 12 – Расчётная схема нагружения и план сил группы звеньев 2,3.
На группу действуют следующие силы:  ,
,  - силы тяжести звеньев;
- силы тяжести звеньев;  ,
,  - равнодействующие силы инерции точек звеньев, приложенные в центре инерции Т 2 и в центре качания К 3 соответственно; реакция
- равнодействующие силы инерции точек звеньев, приложенные в центре инерции Т 2 и в центре качания К 3 соответственно; реакция  , равная по величине известной реакции
, равная по величине известной реакции  , но противоположно ей направленная; а также реакции шарниров
, но противоположно ей направленная; а также реакции шарниров  и
и  , которые раскладываем на нормальные
, которые раскладываем на нормальные 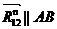 и
и  и тангенциальные
и тангенциальные  и
и  составляющие.
составляющие.
Составляем уравнения равновесия сил в виде суммы моментов всех сил, действующих на звенья 2 и 3 относительно точки В.



Давления 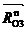 и
и  найдем, построив план сил согласно векторному уравнению равновесия группы в масштабе
найдем, построив план сил согласно векторному уравнению равновесия группы в масштабе 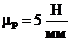 ,
,
 .
.
Из произвольной точки на чертеже откладываем вектор  , затем последовательно пристраиваем векторы сил
, затем последовательно пристраиваем векторы сил  ,
,  ,
,  ,
,  ,
, 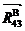 ,
,  ,
,  ,
,  , соблюдая последовательность, масштаб и направление. Далее из начала вектора
, соблюдая последовательность, масштаб и направление. Далее из начала вектора  проводим линию параллельную BO 1, а из конца вектора
проводим линию параллельную BO 1, а из конца вектора  линию параллельную AB, на пересечении которых получим точку, которая замыкая векторный многоугольник, из которого определяем направления реакции
линию параллельную AB, на пересечении которых получим точку, которая замыкая векторный многоугольник, из которого определяем направления реакции  ,
,  ,
,  ,
,  и их величины, замеряя длины соответствующих отрезков и умножаем их на масштаб
и их величины, замеряя длины соответствующих отрезков и умножаем их на масштаб  .
.

Более точные значения давлений  ,
,  ,
,  ,
,  найдем записав уравнения равновесия сил в аналитической форме, используя условия:
найдем записав уравнения равновесия сил в аналитической форме, используя условия: 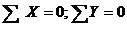 .
.
Давление в шарнире 2,3 является замыкающей стороной многоугольника, построенного на векторах сил, приложенных к звену 2.

3.4.5.2.3. Силовой расчет ведущего звена
На ведущее звено 1 действуют реакции  равная по модулю известной реакции
равная по модулю известной реакции  , но противоположная ей по направлению, уравновешивающая сила
, но противоположная ей по направлению, уравновешивающая сила  , создающая уравновешивающий момент
, создающая уравновешивающий момент 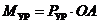 , и реакция шарнира O -
, и реакция шарнира O - 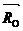 .
.
Уравновешивающую силу определим из уравнения равновесия сил в виде суммы моментов всех сил относительно точки О.
 Откуда
Откуда


Рисунок 13 – Расчетная схема нагружения и план сил ведущего механизма
Для определения реакции в шарнире О составим векторное уравнение равновесия сил, действующих на ведущее звено:

Строим замкнутый многоугольник сил (Рисунок 13) в масштабе  из которого следует, что
из которого следует, что 
3.4.5.2.4. Определение уравновешивающей силы с помощью «рычага» Н.Е. Жуковского
Для определения уравновешивающей силы с помощью «рычага» Н.Е. Жуковского на план скоростей к соответствующим точкам векторов скоростей точек приложения сил прикладываем повернутые на 900 градусов в одном направлении все силы, действующие на звенья механизма.
Уравновешивающую силу 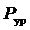 прикладывает в точке а перпендикулярно к вектору
прикладывает в точке а перпендикулярно к вектору  , (Рисунок 13).
, (Рисунок 13).

Рисунок 13 - Проверка методом Жуковского
Из уравнения равновесия «рычага» (плана скоростей) в виде суммы моментов всех сил относительно полюса плана скоростей P найдем величину уравновешивающей силы  .
.


Откуда

3.4.5.2.5. Определение уравновешивающего момента
а) методом планов сил
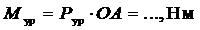
б) методов «рычага» Н.Е. Жуковского

Сравним результаты определения уравновешивающего момента, считая метод планов сил более точным, и определим погрешность

4.Синтез привода
4.1 Синтез эвольвентной зубчатой передачи
Синтез эвольвентной зубчатой передачи производится в следующей последовательности:
1. Производится определение коэффициентов смещения инструмента по таблицам или блокирующим контурам.
2. Производится расчет всех геометрических параметров зубчатых колес.
Масштаб построения выбирается таким образом, чтобы высота зуба на чертеже была не менее 45 мм. Эвольвентный профиль зубьев строится в соответствие с рекомендациями /1/. Вычерчиваются по 3 зуба на каждом колесе. Чертеж зацепления занимает площадь в 0,5…0,7 листа формата А1.
3. Производится расчет и вычерчивание кривых относительного скольжения зубьев. Показываются рабочие участки профилей зубьев, рабочая и теоретическая части линии зацепления, размеры диаметров всех окружностей, угол зацепления.
4.1.1. Построение эвольвентной зубчатой передачи.
Исходными данными для расчета являются модуль зацепления и значения чисел зубьев зубчатого колеса и шестерни, а так же угол профиля зубчатой рейки ( ). Коэффициенты смещения для неравносмещенного зацепления
). Коэффициенты смещения для неравносмещенного зацепления  и коэффициент обратного смещения
и коэффициент обратного смещения  определяются с помощью блокирующего контура (Приложение В) или специальных таблиц (Приложение Г). Коэффициент высоты зуба
определяются с помощью блокирующего контура (Приложение В) или специальных таблиц (Приложение Г). Коэффициент высоты зуба  , коэффициент радиального зазора
, коэффициент радиального зазора  .
.
Коэффициент  отклонения межцентрового расстояния определяем по формуле
отклонения межцентрового расстояния определяем по формуле  .
.
Монтажный угол зацепления определяется с помощью специальной номограммы (Приложение Б).
Остальные параметры зацепления определяются расчетом по следующим формулам:
Шаг зацепления 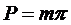 .
.
Радиусы делительных окружностей:  .
.
Толщина зуба по делительной окружности 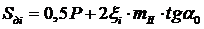 .
.
Радиусы окружностей впадин:  .
.
Межцентровое расстояние:  .
.
Радиусы начальных окружностей: 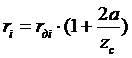 .
.
Глубина захода зубьев:  .
.
Высота зуба 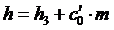 .
.
Радиусы окружностей выступов:  .
.
Масштаб построения 
Построение производится в следующей последовательности:
· Откладывается межцентровое расстояние О1О2 = А.
· Откладывается радиус начально






