Решение:
Пусть  и
и 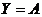 .
.
По определению равенства множеств покажем, что  и
и 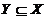 , т.е.
, т.е.  .
.
Пусть  , т.е. по определению объединения и пересечения множеств имеем:
, т.е. по определению объединения и пересечения множеств имеем:
 , т.е.
, т.е. 
Пусть 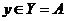 , т.е. по определению объединения и пересечения множеств имеем:
, т.е. по определению объединения и пересечения множеств имеем:
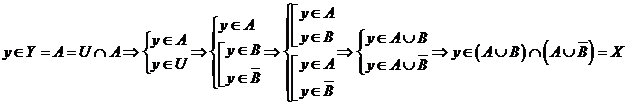 , т.е.
, т.е. 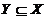 .
.
Т.к.  и
и 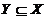 , то
, то  , т.е.
, т.е. 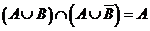 . Ч.т.д.
. Ч.т.д.
5. Пусть 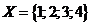 . Отношение
. Отношение  задано характеристическим свойством:
задано характеристическим свойством:

Задать отношение другими возможными способами. Выяснить, какими свойствами оно обладает.
Решение:
Отношение R можно задать перечислением всех элементов:
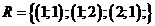 .
.
Область определения отношение R: 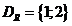 ;
;
Область значений отношение R: 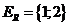 .
.
Наглядно представить отношение R можно с помощью графика:

С помощью схемы:

С помощью графа:

С помощью матрицы отношения:

Выясним, какими свойствами обладает отношение.
Рефлексивность.
При 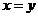 условие
условие  - не выполняется
- не выполняется  - т.е. отношение R не является рефлексивным;
- т.е. отношение R не является рефлексивным;  и не является антирефлексивным.
и не является антирефлексивным.
Симметричность.
Пусть  . Составим пару
. Составим пару 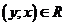 и для нее проверим характеристическое свойство отношения:
и для нее проверим характеристическое свойство отношения:  выполняется. Т.е. отношение
выполняется. Т.е. отношение  - симметрично.
- симметрично.
Транзитивность: пусть  и
и  , т.е.
, т.е.  и
и  выясним выполняется ли неравенство
выясним выполняется ли неравенство 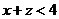 .
.
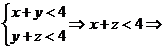
 . Т.е. отношение
. Т.е. отношение  - транзитивно.
- транзитивно.
Отношение R обладает свойствами симметричности и транзитивности, следовательно, не является отношением эквивалентности.
Дано множество и отношение. Показать, что отношение R является отношением порядка. Построить диаграмму Хассе частично упорядоченного множества. Существует ли в множестве X наибольший и наименьший элементы? Существуют ли несравнимые элементы?
Решение:
Покажем, что отношение R рефлексивно, антисимметрично и транзитивно. Рефлексивность имеет место, так как любое число является своим делителем, т.е. 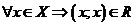 .
.
Пусть одновременно выполняются условия:  и
и 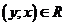 . Тогда
. Тогда 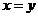 . Действительно,
. Действительно,  означает, что
означает, что  – делитель
– делитель  , т.е. найдется целое число
, т.е. найдется целое число 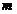 такое, что
такое, что  . Одновременно найдется целое число
. Одновременно найдется целое число  такое, что
такое, что  . Отсюда
. Отсюда  и
и 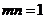 . Последнее равенство выполняется при
. Последнее равенство выполняется при  или
или 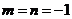 , но все элементы множества X – положительные числа, и второй случай невозможен. Следовательно,
, но все элементы множества X – положительные числа, и второй случай невозможен. Следовательно,  , т.е.
, т.е. 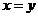 , и отношение R антисимметрично.
, и отношение R антисимметрично.
Пусть  и
и  , значит, найдутся
, значит, найдутся  такие, что
такие, что  ,
,  . Тогда
. Тогда  , где
, где  . Следовательно,
. Следовательно,  является делителем
является делителем  и
и  . Отношение R транзитивно.
. Отношение R транзитивно.
Отношение R рефлексивно, антисимметрично и транзитивно, т.е. является отношением порядка. Построим диаграмму Хассе частично упорядоченного множества  . На первом уровне диаграммы поместим элементы
. На первом уровне диаграммы поместим элементы 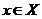 не имеющие других делителей, кроме себя (
не имеющие других делителей, кроме себя (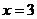 и
и 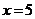 ). На втором уровне – элементы
). На втором уровне – элементы 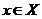 , не имеющие других делителей, кроме себя и элементов нижнего уровня
, не имеющие других делителей, кроме себя и элементов нижнего уровня  . На третьем уровне – элементы
. На третьем уровне – элементы 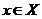 , не имеющие других делителей, кроме себя и элементов второго и первого уровня
, не имеющие других делителей, кроме себя и элементов второго и первого уровня  . Соединяем отрезком элементы соседних уровней, если элемент нижнего уровня является делителем элемента соседнего верхнего уровня.
. Соединяем отрезком элементы соседних уровней, если элемент нижнего уровня является делителем элемента соседнего верхнего уровня.

Диаграмма Хассе построена.
Пара элементов  тогда и только тогда, когда двигаясь по диаграмме только вверх, мы можем пройти от элемента
тогда и только тогда, когда двигаясь по диаграмме только вверх, мы можем пройти от элемента  до элемента
до элемента  . По диаграмме Хассе легко обнаружить несравнимые элементы: 3 и 5. Наибольшим элементом является
. По диаграмме Хассе легко обнаружить несравнимые элементы: 3 и 5. Наибольшим элементом является  (для всех
(для всех 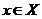 выполнено условие «
выполнено условие « является делителем 30»). Наименьшего элемента нет, но есть два минимальных
является делителем 30»). Наименьшего элемента нет, но есть два минимальных  и
и  .
.
7. Заданы отношения  и
и  :
:
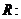

| 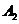
|

| 
|

| 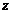
|

| 
|
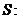
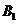
| 
| 
|

| 
| 
|

| 
| 
|

| 
| 
|
Записать обозначения операций реляционной алгебры и выполнить их:
а) проекция отношения S на список (2,1);






