Вариант 8.
Решить задачу, используя диаграмму Эйлера-Венна.
В одной из студентческих групп все студенты умеют программировать. Десять человек умеют работать на Бейсеке. 10 на Паскале, 6 на Си. Два языка знают: 6 человек Бейсик и Паскаль, 4 – Паскаль и Си, 3 – Бейсик и Си. Один человек знает все три языка. Сколько студентов в группе?
Решение:
В задаче идет речь о следующих множествах:
U - – множество студентов в группе;
А – множество студентов умеющие работать на Бейсик;
В – множество студентов умеющие работать на Паскаль;
С – множество студентов умеющие работать на Си.
По условию задачи:
10 человек умеют работать на Бейсик т.е. 
;
10 человек умеют работать на Паскаль, т.е. 
6 человек умеют работать на Си, т.е. 
;
6 человек умеют работать на Бейсик и Паскаль, т.е. 
;
4 человека умеют работать на Паскаль и Си, т.е. 
;
3 человека умеют работать на Бейсик и Си, т.е. 
;
1 человек умеет работать на всех трех языках, т.е. 
.
Требуется найти число число студентов в группе, т.е. 
.
Перенесем эти данные на диаграмму Эйлера-Венна.
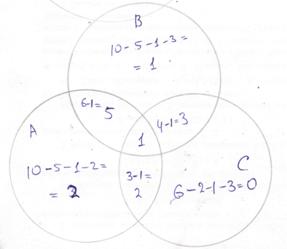
Тогда 
.
Ответ:.
Задано универсальное множество и множества,,. Записать булеан множества X, любое разбиение множества Y, покрытие множества Z. Выполнить действия.
Решение:
Для нахождения множества 
выполним операции над множествами в следующем порядке:
1) 
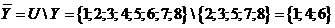- по определению операции отрицания; 2) 
- по определению операции дополнения;
3) 
- по определению операции пересечения.
Итак, 
.
Для построения булеана множества X воспользуемся двоичной записью числа.
Т.к. множество Х содержит 5 элементов, то его булеан содержит 
подмножеств. Будем записывать номер подмножества пятиразрядным двоичным числом от 0 до 31, включая в подмножество только те элементы, которым соответствует единица в двоичном разряде. Результаты внесем в таблицу:
| № подмножества | Двоичная запись номера | Подмножества множества 
| № подмножества | Двоичная запись номера | Подмножества множества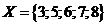 
|
| 0 | 00000 | 
| 16 | 10000 | 
|
| 1 | 00001 | 
| 17 | 10001 |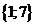 
|
| 2 | 00010 |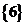 
| 18 | 10010 | 
|
| 3 | 00011 |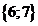 
| 19 | 10011 | 
|
| 4 | 00100 | 
| 20 | 10100 | 
|
| 5 | 00101 |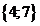 
| 21 | 10101 | 
|
| 6 | 00110 |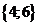 
| 22 | 10110 | 
|
| 7 | 00111 | 
| 23 | 10111 |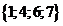 
|
| 8 | 01000 | 
| 24 | 11000 |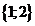 
|
| 9 | 01001 | 
| 25 | 11001 | 
|
| 10 | 01010 | 
| 26 | 11010 | 
|
| 11 | 01011 |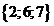 
| 27 | 11011 | 
|
| 12 | 01100 |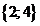 
| 28 | 11100 |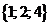 
|
| 13 | 01101 |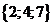 
| 29 | 11101 | 
|
| 14 | 01110 | 
| 30 | 11110 | 
|
| 15 | 01111 | 
| 31 | 11111 | 
|
Итак, в булеан множества Х включаем пустое множество, само множество Х, все одноэлементные подмножества, все двухэлементные подмножества множества Х, все трехэлементные подмножества множества Х, все четырехэлементные подмножества множества Х:
B(X)= ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; 
; ; ; ; ; ; ; ; ; .
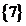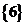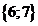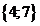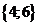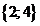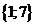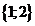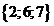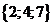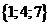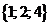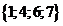Для множества Y построим разбиение, состоящее из трех блоков 
например, таким образом:
.
Определение разбиения выполняется: множества 
не пусты, не пересекаются 
, их объединение равно множеству Y: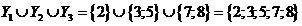 
.
Для построения покрытия выберем подмножества 
и 
. Полученная система множеств 
состоит из двух блоков, объединение которых равно множеству Z: 
.
Упростить, используя законы и тождества алгебры множеств (перечислить используемые законы):.
Решение:
Будем считать операция пересечения имеет более высокий приоритет, чем объединение множеств.
Пользуясь этим правилом, определим порядок действий.
1) По закону дистрибутивности:
.
2) По закону ассоциативности:
.
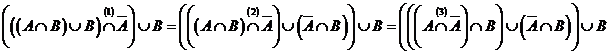3) По свойству пустого множества:
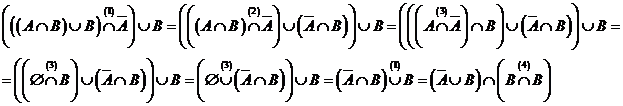
4) По закону идемпотентности:
Ответ:.
