Московский автомобильно-дорожный
Государственный технический университет
(МАДИ)
Кафедра строительной механики
УТВЕРЖДАЮ
ЗАВ. КАФЕДРОЙ
СТРОИТЕЛЬНОЙ МЕХАНИКИ
МАДИ (ГТУ)
Д.Т.Н. ПРОФЕССОР
И.В. Демьянушко
Задания по сопротивлению материалов
И технической механике
Для студентов заочного факультета
Второй семестр
ЗАДАНИЕ № 5а
РАСЧЕТ НА СЛОЖНОЕ СОПРОТИВЛЕНИЕ
(РАСЧЕТ ПРОСТРАНСТВЕННОГО БРУСА)
(для студентов механических специальностей)
Требуется:
1). Построить эпюры изгибающих и крутящих моментов, поперечных и продольных сил;
2). Определить положение опасного сечения и, пользуясь гипотезой прочности потенциальной энергии изменения формы, подобрать размеры сечений брусьев двух типов: трубчатого с отношением диаметров d / D = 0,8 (d - внутренний, D - наружный диаметры) и прямоугольного с отношением сторон h / b =2 (h - большая, b - меньшая стороны прямоугольника). Принять допускаемое напряжение [ s ] = 100 МПа.
3). Для прямоугольного сечения построить:
а). Эпюры нормальных напряжений: от продольной силы - s z (N);
от изгибающего момента Мх - s z (M х), от изгибающего момента Му - s z (M у);
b). Эпюры касательных напряжений –от крутящего момента М z - t (Mz);от поперечной силы Q х - t (Q х); от поперечной силы Q у - t (Q у);
с). Указать опасную точку сечения.
Исходные данные
| Номер группы | Нагрузка | Размеры, [м] | |||||
| р 1, [кН] | Р2, [кН ] | Р3, [кН] | Q, [кН/м] | а | b | с | |
| 3ЗАТ1 | 2,0 | 4,0 | 2,0 | 1,0 | 0,6 | 0,8 | 0,6 |
| 3ЗАТ2 | 4,0 | 5,0 | 8,0 | 2,0 | 0,5 | 0,8 | 0,4 |
| 2ЗбСс1 | 3,0 | 4,0 | 7,0 | 2,5 | 0,4 | 0,6 | 0,7 |
| 2ЗбСс2 | 6,0 | 5,0 | 8,0 | 3,0 | 0,6 | 0,8 | 0,8 |
| 2ЗбСс3 | 8,0 | 6,0 | 8,0 | 4,0 | 0,8 | 1,0 | 0,7 |
| 7,0 | 10,0 | 6,0 | 5,0 | 0,6 | 0,9 | 0,8 | |
| 10,0 | 9,0 | 5,0 | 5,0 | 0,6 | 1,0 | 0,7 | |
| 9,0 | 5,0 | 7,0 | 3,5 | 0,8 | 0,9 | 0,9 | |
| 6,0 | 8,0 | 10,0 | 5,5 | 0,7 | 1,0 | 1,0 | |
Задание № 5-б
Расчет на сложное сопротивление
(внецентренное сжатие)
Для студентов строительных специальностей)_
Требуется:
Определить нормальные напряжения по подошве призматического тела высотой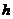 
, сечение которого задано.
Порядок выполнения
1. Изобразить тело в аксонометрии
2. Найти площадь сечения, положение центра тяжести сечения, главные центральные моменты инерции и квадраты радиусов инерции.
3. Определить внутренние силы по подошве тела, найти центр давления, нанести нулевую линию и вычислить напряжение в центре тяжести сечения. Построить плоскую эпюру напряжений в нижнем сечении.
4. Написать уравнение и вычислить нормальные напряжения во всех угловых точках контура подошвы. По вычисленным ординатам построить пространственную эпюру напряжений.
5. Построить ядро сечения и нанести на нем координаты центра давления.
Исходные данные
| Номер |
| Высота
[ м ] | Плотность [ т/м3 ] | |||
| группы | 
| 
| 
| |||
| 2ЗбДс1 | 200 | 650 | 550 | 3,0 | 1,40 | |
| 2ЗбДс2 | 250 | 700 | 500 | 2,6 | 1,9 | |
| 3ЗбДп | 300 | 750 | 450 | 2,5 | 1,2 | |
| 2ЗбДп | 350 | 200 | 400 | 3,2 | 1,5 | |
| 1ЗбДс1 | 400 | 250 | 750 | 2,8 | 1,6 | |
|
| 450 | 300 | 700 | 2,0 | 1,7 | |
|
| 500 | 350 | 650 | 2,0 | 1,3 | |
|
| 550 | 400 | 350 | 2,2 | 1,1 | |
|
| 600 | 450 | 300 | 1,8 | 1,89 | |
Силы [кН]
ЗАДАНИЕ № 6а
(Для студентов механических специальностей)
РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ РАМЫ МЕТОДОМ СИЛ
Требуется:
построить эпюры изгибающих моментов, поперечных и продольных сил в заданной системе. В процессе решения выполнить необходимые контроли вычислений.
Порядок выполнения:
1). Найти степень статической неопределимости и выбрать основную систему;
2). Построить единичные и грузовые эпюры и вычислить единичные и грузовые перемещения;
3). Построить суммарно единичную эпюру и произвести контроли сумм единичных и грузовых перемещений (контроли №№ 1 и 2);
4). Составить и решить систему канонических уравнений метода сил. Подставить результат в исходную систему (контроль № 3);
5). Построить эпюру изгибающих моментов и проверить равновесие узлов (контроль № 4);
6). Выполнить универсальный деформационный контроль решения (контроль № 5);
7). Построить эпюру поперечных сил дифференцированием эпюры изгибающих моментов;
8). Построить эпюру продольных сил способом вырезания узлов;
9). Отбросив связи и заменив их реакциями, проверить равновесие системы в целом (контроль № 6).
Исходные данные
| № группы | l 1 | l 2 | а | Н | 9 | k | Р в долях ql |
| 3ЗАТ1 | 21 | 21 | 1 | 21 | 1|2 | 2 | 3 |
| 3ЗАТ2 | 41 | 61 | 21 | 41 | 1|2 | 3 | 2 |
| 2ЗбСс1 | 61 | 91 | 31 | 61 | 1|3 | 2 | 3 |
| 2ЗбСс2 | 1 | 1 | 1 | 1 | 1 | 2 | 1 |
| 2ЗбСс3 | 21 | 41 | 21 | 21 | 1|2 | 1 | 3 |
| 31 | 61 | 21 | 61 | 1|3 | 3 | 3 | |
| 41 | 21 | 21 | 21 | 1|2 | 2 | 2 |
ЗАДАНИЕ № 6б
