Положение точек объекта (местности) по снимкам определяют в прямоугольной пространственной системе координат OXYZ. В зависимости от решаемой задачи в качестве этой системы координат используют:
- государственную картографическую систему координат (в России – Гаусса – Крюгера);
- геоцентрическую систему координат;
- произвольную систему координат, связанную с характерными точками объекта (местности).
Положение и ориентацию системы координат снимка (или, что то же самое – снимка) в системе координат объекта OXYZ определяют элементы внешнего ориентирования снимка.
Положение центра проекции S в системе координат объекта определяют его координаты Xs,Ys,Zs.
Угловая ориентация системы координат снимка относительно системы координат объекта определяется ортогональной матрицей:
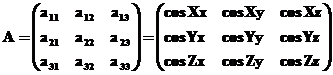(1.2.1)
В матрице А элементы (направляющие косинусы) а ij являются косинусами пространственных углов между осями системы координат объекта OXYZ и снимка Sxyz.
Направляющие косинусы являются координатами единичных векторов (ортов), совпадающих с осями координат снимка в системе координат объекта.
Вследствие особых характеристик ортогональной матрицы:
А-1=Ат,
а Ат A = Е = 
.
Или, раскрыв последнее уравнение видно, что элементы этой матрицы связаны между собой шестью независимыми уравнениями:
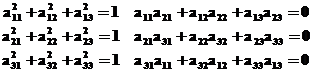
поэтому в матрице направляющих косинусов независимы только 3 элемента, следовательно, элементы этой матрицы являются функцией 3 параметров.
В качестве этих параметров в фотограмметрии используют 3 угла - w, a и À, которые называют угловыми элементами внешнего ориентирования снимка.
Последовательно поворачивая систему координат объекта OXYZ на эти углы вокруг ее осей, можно ориентировать ее параллельно осям системы координат снимка. При этом последовательность и направление вращений могут быть произвольными. Поэтому в фотограмметрии используют различные системы угловых элементов ориентирования снимка.
X
S(O)
w
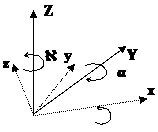a/ b/
Рис. 1.2.
На рис. 1.2 показаны возможные направления вращений вокруг соответствующих осей системы координат SXYZ на углы w, a и À. В первом случае (рис. 1.2а) вращения выполняются против часовой стрелке (правые углы), а во втором случае (рис. 1.2b) - по часовой стрелке (левые углы). Здесь стрелками показаны положительные направления углов.
Рассмотрим наиболее широко используемую систему, в которой система координат объекта OXYZ поворачивается последовательно против часовой стрелки (правые углы) вокруг осей X,Y и Z соответственно на углы w, a и À.
Геометрическая интерпретация угловых элементов внешнего ориентирования показана на рис.1.2.1.
w -поперечный угол наклона. Угол в координатной плоскости YZ между осью Z и проекцией оси z на плоскость YZ;
a - продольный угол наклона. Угол между проекцией оси z на плоскость YZ и осью z;
À - угол разворота снимка. Угол в плоскости снимка Р между следом сечения этой плоскости плоскостью Xz и осью х снимка.
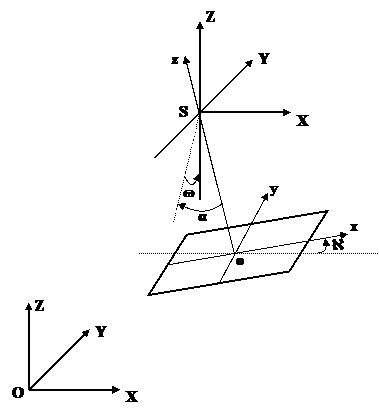
Рис.1.2.1 
Значение элементов aij матрицы А можно получить путем последовательного перемножения матриц составленных для последовательных поворотов системы координат объекта ОХ YZ на углы w, a и À.
В результате поворота системы координат ОХ YZ или что тоже самое системы координат SXYZ на угол w эта система преобразуется в систему координат SX ’Y ’Z ’ (рис.1.2.2)
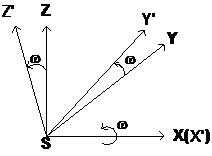
Рис.1.2.2
В соответствии с выражением 1.2.1 матрица
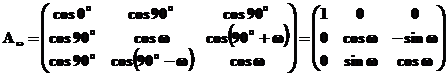
В результате поворота на угол a система координат SX ’Y ’Z ’ преобразуется в систему координат SX ”Y ”Z ” (рис.1.2.3).
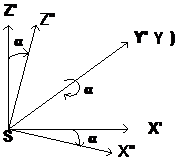
Рис.1.2.3
В соответствии с выражением 1.2.1 матрица
В результате поворота системы координат SX ”Y ”Z ” на угол À эта система преобразуется в систему координат снимка Sxyz (рис.1.2.4).
 |
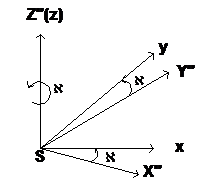Рис.1.2.4
В соответствии с выражением 1.2.1 матрица
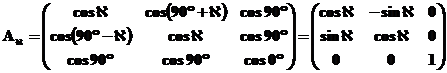
В результате перемножения матриц
,
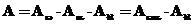получим значения элементов aij, как функции углов w, a и À
(1.2.2)
Если известны значения направляющих косинусов aij, то из выражений (1.2.2) можно получить значения углов w,a,À.
(1.2.3)
