Первой стадией растворения любого полимера является его набухание - процесс поглощения полимером низкомолекулярной жидкости, сопровождающийся увеличением объема полимера и изменением конформаций его макромолекул.
Если процесс растворения самопроизвольно прекращается на стадии набухания, то говорят об ограниченном набухании, которое может быть обусловлено двумя причинами: ограниченным сродством полимера к растворителю и образованием сшитого полимера. Набухание характеризуют степенью набухания 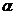 , которую определяют как количество поглощенной полимером жидкости, отнесенное к единице массы или объема полимера:
, которую определяют как количество поглощенной полимером жидкости, отнесенное к единице массы или объема полимера:
 (7.1)
(7.1)
где  ,
, 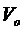 - масса и объем исходного полимера;
- масса и объем исходного полимера;
 ,
,  - масса и объем набухшего полимера.
- масса и объем набухшего полимера.
Скорость набухания лимитируется скоростью взаимной диффузии компонентов системы и для полимеров, находящихся в исходном высокоэластическом состоянии, обычно удовлетворительно описывается кинетическим уравнением первого порядка:
 (7.2)
(7.2)




где  – константа скорости набухания;
– константа скорости набухания;
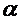 max - максимальная степень набухания;
max - максимальная степень набухания;
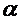
 - степень набухания в момент времени
- степень набухания в момент времени  .
.
После интегрирования этого уравнения получим:
 (7.3)
(7.3)
По тангенсу угла наклона прямолинейной зависимости  от времени можно определить константу скорости набухания.
от времени можно определить константу скорости набухания.
В случае несшитых полимеров при изменении условий (температуры, концентрации и др.) ограниченное набухание может перейти в неограниченное, при этом макромолекулы диффундируют в растворитель вплоть до образования гомогенного раствора.
Одним из распространенных методов определения молекулярной массы высокомолекулярных соединения является осмометрический метод. В случае растворов полимеров уравнение состояния связывает осмотическое давление с температурой, концентрацией раствора и индивидуальными характеристиками компонентов. Приведенное осмотическое давление растворов полимеров описывается уравнением:
 (7.4)
(7.4)
где  - осмотическое давление,
- осмотическое давление,
А1=1/M, А2, А3 – соответственно первый, второй,третий вириальные коэффициенты; M – молекулярная масса полимера.
Коэффициент А2 существенно зависит от природы растворителя и является удобной характеристикой термодинамического качества растворителя, т.е. термодинамического сродства к растворителя полимеру. В хороших растворителях А2 > 0, в плохих – А2 < 0. При А2 = 0 раствор полимера ведет себя как идеальный. Измеряя зависимость  от с и строя ее в координатах уравнения (7.4), можно определить значения М и А2.
от с и строя ее в координатах уравнения (7.4), можно определить значения М и А2.
Вискозиметрический метод определения молекулярной массы является наиболее простым из существующих методов. Растворы полимеров характеризуются следующими вискозиметрическими параметрами:
относительной вязкостью -  ;
;
удельной вязкостью -  ;
;
приведенной вязкостью -  ;
;
характеристической вязкостью -  ,
,
где 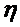 и
и  - вязкости
- вязкости  испытуемого раствора полимера и чистого растворителя, определенные при одинаковых условиях; с – концентрация раствора.
испытуемого раствора полимера и чистого растворителя, определенные при одинаковых условиях; с – концентрация раствора.
Характеристическая вязкость полимера в любом растворителе описывается следующим выражением:
 (7.5)
(7.5)
где М - молекулярная масса полимера; постоянная К=10-2-10-5 и зависит от температуры и природы полимера и растворителя.
Показатель " 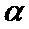 " связан с конформацией макромолекулы в растворе и зависит от всех факторов, влияющих на конформацию цепи. Для компактных частиц типа эйнштейновских
" связан с конформацией макромолекулы в растворе и зависит от всех факторов, влияющих на конформацию цепи. Для компактных частиц типа эйнштейновских  = 0; для гауссовых клубков в
= 0; для гауссовых клубков в  -условиях
-условиях  = 0,5; для гибких макромолекул в хороших растворителях
= 0,5; для гибких макромолекул в хороших растворителях  = 0,6-0,8; для жестких макромолекул, т.е. протекаемых клубков
= 0,6-0,8; для жестких макромолекул, т.е. протекаемых клубков 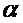 = 1,0-1,5; для палочкообразных частиц
= 1,0-1,5; для палочкообразных частиц  - 2,0.
- 2,0.
Таким образом, в общем случае “  ” изменяется в пределах 0 <
” изменяется в пределах 0 < 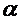 < 2,0. Уравнение (7.6) носит название уравнения Марка-Куна-Хаувинка. Оно справедливо для большого числа полимерных веществ и является основным уравнением вискозиметрии разбавленных растворов полимеров.
< 2,0. Уравнение (7.6) носит название уравнения Марка-Куна-Хаувинка. Оно справедливо для большого числа полимерных веществ и является основным уравнением вискозиметрии разбавленных растворов полимеров.
Очевидно, что для расчета молекулярной массы полимера по формуле (7.6) необходимо предварительное определение констант К и  . Поэтому вискозиметрический метод определения молекулярной массы полимеров является лишь относительным. Константы К и
. Поэтому вискозиметрический метод определения молекулярной массы полимеров является лишь относительным. Константы К и 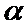 находят, определяя молекулярные массы серии узких фракций полимера с помощью какого-либо абсолютного метода (осмометрии, светорассеяния и др.).
находят, определяя молекулярные массы серии узких фракций полимера с помощью какого-либо абсолютного метода (осмометрии, светорассеяния и др.).
Зависимость приведенной вязкости от концентрации раствора полимера описывается уравнением Хаггинса:
 (7.7)
(7.7)
где  - константа Хаггинса, характеризующая взаимодействие макромолекул в данном растворителе.
- константа Хаггинса, характеризующая взаимодействие макромолекул в данном растворителе.
В хороших растворителях  =0,2-0,3, в плохих-
=0,2-0,3, в плохих-  >0,5.
>0,5.
Характеристическая вязкость определяет поведение изолированных макромолекул. Она представляет собой меру потерь на трение изолированных макромолекул о растворитель при их вращении в результате поступательного движения в потоке с градиентом скорости, отличным от нуля. Характеристическая вязкость зависит от размеров макромолекул в растворе, от природы растворителя и температуры раствора. В хорошем растворителе клубок набухает и вязкость увеличивается.
Оптический метод определения молекулярной массы основан на рассеянии света растворами ВМС. Дебаем был предложен метод определения молекулярной массы, основанный на измерении интенсивности рассеянного света (мутности) разбавленных растворов ВМС. Уравнение Дебая для оптического метода имеет вид:
 (7.8)
(7.8)
где А2 -второй вириальный коэффициент в уравнении состояния растворов полимеров (7,4); H –константа для данной системы полимер – растворитель;

Для определения молекулярной массы измеряют мутность раствора для нескольких концентраций, строят график зависимости  от концентрации, который представляет прямую линию. По величине отрезка, отсекаемого этой прямой на ординате [
от концентрации, который представляет прямую линию. По величине отрезка, отсекаемого этой прямой на ординате [  ] находят величину, обратную величине молекулярной массы и вычисляют молекулярную массу ВМС.
] находят величину, обратную величине молекулярной массы и вычисляют молекулярную массу ВМС.
 (7.9)
(7.9)
Найденное значение для полидисперсных ВМС представляет средневесовое значение молекулярной массы.
Метод Дебая применим только для определения молекулярной массы сравнительно низкомолекулярных полимеров, размер молекул которых не превышает 10-7 м, так как он должен быть меньше 1/20 длины волны рассеянного света. Это условие, однако, обычно соблюдается для растворов высокополимеров, в которых макромолекулы свернуты в клубок.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
При набухании бутадиен-стирольного каучука в веретенном масле получены следующие экспериментальные данные:
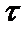 ,мин ,мин
| 0 | 50 | 100 | 200 | 400 | 600 |
| m×103,г | 3,684 | 8,657 | 11,605 | 15,473 | 19,525 | 20,004 |
t- время;
m – масса набухшего полимера
Определите графическим способом константу скорости набухания К.
РЕШЕНИЕ При ограниченном набухании полимеров степень набухания изменяется во времени в соответствии с уравнением

Интегрируя это уравнение, получим

Зависимость  от
от 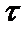 является линейной.
является линейной.
Рассчитываем данные для построения графика этой зависимости:
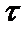 ,мин ,мин
| 50 | 100 | 200 | 400 | 600 |
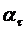
| 1,33 | 2,15 | 3,2 | 4,3 | 4,43 |

| 3,1 | 2,28 | 1,23 | 0,13 | |

| 1,13 | 0,824 | 0,207 | -2,04 |
Из графика (рис. 5) находим К. -К = tg 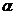 К=6,45.10-3 мин-1
К=6,45.10-3 мин-1
 |
Рис. 5. Определение константы скорости набухания каучука в веретенном масле.
2. Определите молекулярную массу поливинилхлорида и значение второго вириального коэффициента А2, используя экспериментальные данные, полученные методами светорассеяния. Величина постоянной Н=6×10-13, растворитель циклогексан.
| Концентрация раствора с, кг/м3 | 1,69 | 2,12 | 2,66 | 3,26 | 3,75 |
Мутность раствора,  м-1 м-1
| 8,54 | 10,25 | 12,67 | 14,80 | 16,75 |
РЕШЕНИЕ По уравнению Дебая мутность  раствора полимера связана с его массовой концентрацией с и молекулярной массой М следующим образом:
раствора полимера связана с его массовой концентрацией с и молекулярной массой М следующим образом:

Рассчитываем значения  и строим их зависимость от c (рис.6).
и строим их зависимость от c (рис.6).
| C,кг/м3 | 1,69 | 2,12 | 2,66 | 3,26 | 3,75 |
H.c/  .104,кг/м3 .104,кг/м3
| 1,19 | 1,24 | 1,26 | 1,32 | 1,34 |
Экстраполируя зависимость на значение с =0, находим 1/М = 1,05.104,М = 95238.

Рис.6. Зависимость приведенной мутности от концентрации раствора полимера






