Устойчивость дисперсной системы характеризуется неизменностью во времени двух ее основных параметров: дисперсности и равномерного распределения дисперсной фазы в среде. В связи с этим различают седиментационную устойчивость, связанную с сохранением равномерного распределения частиц и агрегативную устойчивость системы, связанную с сохранением размера частиц.
Седиментационной называют устойчивость дисперсной фазы по отношению к силе тяжести, которая зависит от интенсивности теплового движения частиц, влияния на них гравитационного поля и вязкости дисперсионной среды. Коллоидные системы, особенно лиозоли,имеющие частицы размера 10-9-10-7 м обладают достаточно высокой седиментационной устойчивостью. Микрогетерогенные системы, например суспензии или эмульсии, относятся к седиментационно неустойчивым системам.
Агрегативная устойчивость - способность системы к сохранению дисперсности и индивидуальности частиц дисперсной фазы. Лиофобные коллоидные системы являются термодинамически неустойчивыми, так как частицы дисперсной фазы склонны к коагуляции – слипанию частиц, образованию крупных агрегатов с потерей седиментационной и фазовой устойчивости. Причины агрегативной неустойчивости заключены в самих признаках коллоидного состояния системы - ее гетерогенности и высокой дисперсности. Совокупность этих признаков обусловливает достаточно высокое значение свободной поверхностной энергии (∆F > 0), делающей систему неустойчивой.
Снижение поверхностной энергии, а значит более устойчивое состояние системы, возможно либо в результате уменьшения поверхности (коагуляция), либо в результате уменьшения поверхностного натяжения за счет адсорбции третьего компонента – стабилизатора на границе раздела фаз (стабилизация). Следовательно, присутствие в системе стабилизатора может обеспечивать постоянство размера частиц и является необходимым условием существования лиофобной коллоидной системы.
Устойчивость дисперсной системы определяется балансом сил притяжения и сил отталкивания. Общая энергия взаимодействия между двумя пластинами, приходящаяся на единицу их площади, равна
(6.1)
Силы притяжения обусловлены межмолекулярными силами Ван-дер-Ваальса, из которых наиболее универсальными являются лондовские силы дисперсионного взаимодействия, изменяющиеся по степенному закону. По теории ДЛФО (Дерягин, Ландау, Фервей, Овербек), учитывающей только электростатическую составляющую расклинивающего давления, энергия отталкивания убывает с расстоянием по экспоненциальному закону.
Для области малых электрических потенциалов суммарная энергия взаимодействия частиц равна
(6.2)
где 
-электрический потенциал диффузного слоя;
-величина, обратная толщине диффузного слоя;
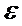- диэлектрическая проницаемость дисперсионной среды;
-электрическая постоянная.
-константа Гамакера;
- расстояние между частицами;
- показатель степени, изменяющийся от I до 3;
При больших потенциалах и расстояниях между частицами эта энергия определяется соотношением
(6.3)
где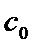 
- концентрация противоионов в дисперсионной среде;
- постоянная, определяемая величиной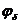 
.
Взаимодействие двух частиц дисперсной фазы принято характеризовать с помощью потенциальных кривых - зависимостей энергии взаимодействия от расстояния (рис.4).
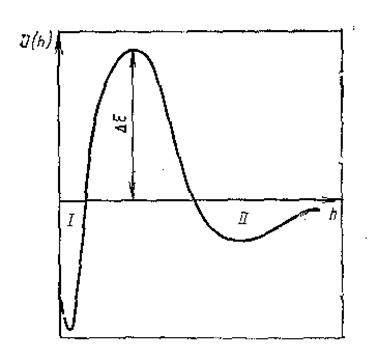
Рис. 4. Зависимость энергии взаимодействия U двух частиц от расстояния h.
Суммарная потенциальная кривая имеет сложный вид. При 
, а 
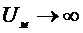. Следовательно, на малых расстояниях преобладает притяжение, поскольку степенная функция убывает значительно медленнее, чем экспонента. В ближнем минимуме происходит необратимая коагуляция частиц, приводящая к образованию конденсационно-кристаллизационный структур, в дальнем - обратимая коагуляция с образованием коагуляционных структур, сохраняющих прослойки среды между частицами. На средних расстояниях преобладают силы отталкивания и система находится в устойчивом состоянии. Возможность сближения частиц в элементарном акте определяется высотой барьера и глубиной ям и зависит от различных внешних воздействий.
Ионностабилизованные коллоидные системы коагулируют при введении электролитов. Коагулирующее действие электролита определяется прежде всего зарядом того иона, знак которого противоположен заряду поверхности коллоидных частиц. Увеличение концентрации электролита в дисперсионной среде приводит к коагуляции, идущей с заметной скоростью лишь при концентрации, превышающей некоторое критическое значение, называемое порогом коагуляции Ск. Ниже этой концентрации (в области медленной коагуляции) скорость коагуляции растет с ростом концентрации до тех пор, пока не достигнет некоторого предела, после которого (в области быстрой коагуляции) перестает зависеть от концентрации электролита.
Сопоставление коагулирующего действия электролитов с их влиянием на электрокинетические свойства коллоидных систем показало, что порог коагуляции соответствует уменьшению электрокинетического потенциала примерно до 30 мВ.
По правилу Щульце-Гарди порог коагуляции определяется в основном валентностью противоионов, так что отношение порогов коагуляции одно-, двух- и трехвалентных противоионов приближенно равно 1:1/20:1/500. По правилу Дерягина – Ландау эти отношения равны 1:1/64:1/729. В лиотропных рядах ионов порог коагуляции уменьшается с увеличением радиуса коагулирующего иона.
Согласно Смолуховскому в случае быстрой коагуляции, можно приближенно считать, что частицы взаимодействуют друг с другом только на расстоянии, близком к расстоянию непосредственного соприкосновения частиц. Тепловое движение частиц дисперсной фазы приводит к их диффузионному сближению друг с другом и как следствие этого - к коагуляции. Для разбавленной системы можно рассматривать процесс коагуляции как совокупность большого числа сближений двух частиц, так как вероятность одновременной встречи трех частиц мала. Теория коагуляции может быть поэтому сведена к теории бимолекулярных реакций. Так как при коагуляции происходит увеличение размеров частиц, необходимо рассматривать цепочку последовательных бимолекулярных реакций между двумя одиночными частицами, одиночной и двойной,одиночной и тройной, двумя двойными и т.д. Поскольку столкновение любой пары частиц уменьшает на единицу число коллоидных частиц в системе, то изменение во времени концентрации коллоидных частиц описывается дифференциальным уравнением:
(6.4)
если объемы частиц отличаются не более чем на порядок величины,можно приближенно считать, что константа скорости коагуляции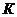 
в уравнении не зависит от размеров частиц и приближенно равна
(6.5) 
где 
- вязкость среды.
Решение уравнения дает
(6.6)
где 
– время половинной коагуляции, представляет собой время, в течение которого число частиц уменьшается вдвое.
Время половинной коагуляции определяется только исходной концентрацией дисперсной системы, вязкостью среды и температурой:
(6.7)
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
1.Определите знак заряда коллоидных частиц и порог коагуляции электролитов, если для того, чтобы вызвать коагуляцию 1·10-5 м3 золя Аl(ОН)3 был израсходован следующий объем раствора электролитов указанной концентрации:
| Электролит | КNОз | Na3Сг04 | Кз[Fе(СN6)] |
| V.106, м3 | 13,3 | 3,4 | 0,074 |
| С, кмоль/м3 | 0,45 | 0.028 | 0.054 |
РЕШЕНИЕ Порог коагуляции электролита определяется по уравнению:
кмоль/м3
Согласно правилам коагуляции электролитами коагуляцию вызывают ионы, заряд которых одинаков с противоионами мицелл. В нашем случае катионы всех электролитов одновалентны, а пороги коагуляции разные, следовательно, коагуляцию вызывают анионы электролитов, валентность которых неодинакова. Поэтому заряд частицы положительный.
2. Порог коагуляции полихлоропренового латекса хлористым натрием составляет 0,28 моль/л. Рассчитайте порог коагуляции для СаС12 и АlCl3, используя правило Шульце-Гарди.
РЕШЕНИЕ По правилу Шульце-Гарди пороги коагуляции, вызываемой электролитами с зарядами противоионов I, 2, 3 находятся в соотношении 1; 1/20; 1/500.
= 1,4.10-2 моль/л;
= 5,6.10-4 моль/л.
3. При изучении коагуляции суспензии бентонитовой глины в воде методом счета частиц в ультрамикроскопе получены следующие данные:
 , с
| 0 | 300 | 500 | 600 | 700 |
| ν.10-14/м3 | 6,0 | 2,97 | 2,25 | 1,95 | 1,8 |
Проверьте применимость уравнения Смолуховского для описания данных по кинетике коагуляции.
РЕШЕНИЕ Согласно теории Смолуховского, время половинной коагуляции не зависит от времени коагуляции. Чтобы проверить применимость теории по экспериментальным данным вычисляется для нескольких значений по уравнению (6.5):
, отсюда 
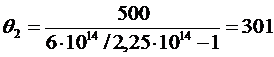с
с
с
с
Величина 
остается постоянной при различных 
, следовательно, в системе происходит быстрая коагуляция и теория Смолуховского применима для описания данного процесса.
4. Рассчитайте и постройте потенциальную кривую взаимодействия сферических частиц диаметром 160 нм в водном растворе NаСl по следующим данным; потенциал 
= 25 мВ; константа Гамакера А= 5,10-20 Дж; параметр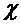 
= 108 м-1 и температура 293 К. Значения суммарной энергии взаимодействия определите при расстояниях I, 3. 5, 10, 20, 40 нм.
РЕШЕНИЕ. Согласно теории устойчивости ДЛФО для слабозаряженных поверхностей и малых расстоянийhр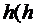 
< 50 нм) суммарная энергия взаимодействия между двумя частицами радиуса рассчитывается по формуле:
Находим значения U при h = I нм
Uэ=2·3,I4·8,85·IО-I2·8I·0,8·IО-7·(2,5·IО-2)2ln(1+е-0,1)= 14,5·10-20 Дж
Дж
U = 14,5.10-20 – 33.10-20 = -18,5 Дж
Аналогично рассчитываем энергию взаимодействия частиц при других расстояниях h:
| ,нм
| 
| 
| 
|  Дж
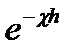
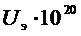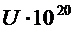|  Дж
|  Дж
|
| 1 | 0,1 | 0,905 | 0,644 | 14,5 | -33 | -18,5 |
| 3 | 0,3 | 0,74 | 0,554 | 12,46 | -11,0 | -1,46 |
| 5 | 0,5 | 0,606 | 0,473 | 10,65 | -6,7 | 3,95 |
| 10 | 1,0 | 0,308 | 0,313 | 7,04 | -3,3 | 3,71 |
| 20 | 2,0 | 0,135 | 0,126 | 2,84 | -1,67 | 1,17 |
| 40 | 4,0 | 0,018 | 0,0178 | 0,4 | -0,83 | -0,43 |
 |
По данным приведенных расчетов строят график зависимостей Uэ, Uм, U от h.
Рис. 5. Зависимость энергии электростатического отталкивания 
, энергии молекулярного притяжения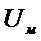 
и суммарной энергии взаимодействия частиц от расстояния.
