ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
Объектом изучения коллоидной химии являются дисперсные системы, обладающие одновременно гетерогенностью и дисперсностью.
В гетерогенных системах на границе раздела фаз существует переходный (межфазный) слой, в котором постепенно меняются свойства и структура при переходе от одной фазы к другой. Межфазный слой обладает набором собственных термодинамических свойств, зависящих от различия свойств образующих его фаз. Молекулы этого слоя втягиваются в соседние фазы с разной интенсивностью, что создает натяжение вдоль поверхности раздела, которое называют поверхностным натяжением на границе раздела конденсированная фаза - газ и межфазным на границе конденсированных фаз. Увеличение этой границы требует затраты энергии по переводу молекул из глубины фазы (более глубокой потенциальной ямы) на поверхность раздела, что эквивалентно избытку свободной энергии, которое является интенсивной величиной, а площадь поверхности раздела Sпл - экстенсивной. Следовательно, общая свободная поверхностная энергия на любой границы раздела будет равна
(1)
Диспергирование (измельчение) конденсированных фаз приводит к увеличению свободной поверхностной энергии и в сильно измельченных системах вносит значительный вклад в общие термодинамические свойства дисперсной системы, который необходимо учитывать. Этот вклад учитывается двумя методами: методом избыточных величин Гиббса и методом слоев конечной толщины Гуггенгейма - Ван-дер-Ваальса.
В методе Гиббса термодинамические свойства межфазного слоя рассматриваются как избытки свойств гетерогенной системы за вычетом свойств чистых фаз:
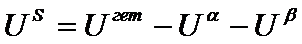(2)
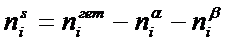(3)
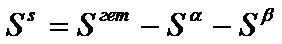(4) и т. д.
Однако в методе Гиббса эти избытки отнесены не к объему слоя (экспериментально практически не определимому), а к единице поверхности раздела фаз, выбранной определенным образом в переходном слое, которую Гиббс назвал разделяющей поверхностью. Таким образом, термодинамические свойства слоя представлены как разность его свойств в реальной и идеализированной системе, где свойства при переходе от одной фазы к другой меняются скачкообразно на разделяющей поверхности.
Используя выражение для объединенного первого и второго закона термодинамики гетерогенной системы и отдельных чистых фаз, Гиббс получил фундаментальное уравнение для межфазного слоя
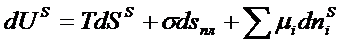(5)
где US -полная энергия межфазного слоя, s - межфазное натяжение, sпл - площадь границы раздела фаз, mi - химический потенциал i – го компонента, niS - число молекул межфазного слоя.
Для уравнения (5) справедливы все соотношения метода термодинамических функций Гиббса, используя которые можно получить и другие фундаментальные уравнения: для энергии Гиббса dGS, Гельмгольца dFS и энтальпии dHS.
Это открывает возможности для получения большого числа термодинамических соотношений для межфазного слоя, наприме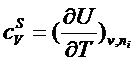р 
, 
и др.
Используя фундаментальное уравнение (5), варьируя интенсивные и экстенсивные величины, можно получить фундаментальное адсорбционное уравнение, устанавливающее связь между изменением межфазного натяжения, составом (через химический потенциал) и температурой:
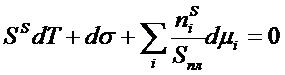(6)
где величины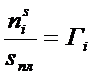 
названа адсорбцией Гиббса.
Для постоянной температуры (6) переходит в изотерму Гиббсовой адсорбции:
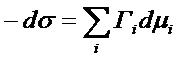(7)
а для двухкомпонентной системы:
(8)
Этого уравнения недостаточно для нахождения адсорбции одного из компонентов (обычно второго растворенного компонента). Поэтому Гиббс выбрал в качестве разделяющей поверхности поверхность, на которой адсорбция растворителя Г1 = 0, и назвал ее эквимолярной. В этом случае, используя выражение для химического потенциала разбавленного раствора, можно получить
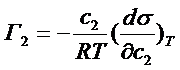(9)
где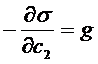 
называют поверхностной активностью, а 
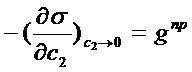– предельной поверхностной активностью, являющейся характеристикой взаимодействия молекул растворителя и растворенного вещества.
Таким образом, в методе Гиббса обязательным является выбор положения разделяющей поверхности в межфазном слое, что аналогично выбору стандартного состояния для химического потенциала, поскольку в переходном слое можно провести сколь угодно много плоскостей, не имеющих толщины.
Существует несколько способов выбора положения разделяющей поверхности; чаще других применяется способ, предложенный самим Гиббсом (Г1 = 0). Применительно к этому случаю удельная свободная энергия Гиббса равна поверхностному натяжению, отсюда
(10)
или
(11)
где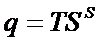 
- скрытая теплота образования новой поверхности.
Соотношение (10) позволяет рассчитать полную поверхностную энергию Us по экспериментально измеренным s и его температурному коэффициенту 
.
Связь между поверхностным натяжением и составом раствора для ПАВ и разбавленных растворов выражается уравнением Шишковского:
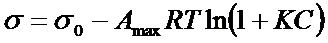(11а)
где s0 - поверхностное натяжение чистого растворителя;
Amax - максимальная адсорбция при полном заполнении монослоя;
K - адсорбционная константа;
C - концентрация ПАВ.
Удельную поверхность можно рассчитать по размеру частиц дисперсной фазы:
(12)
где К - коэффициент формы частицы, d - диаметр частицы, D - ее дисперсность. Для сферических частиц
(13)
Следует заметить, что для плоского поверхностного слоя, как отмечалось выше, величина Гиббсовой адсорбции зависит от выбора положения разделяющей поверхности, а поверхностное натяжение - нет, поскольку плоский поверхностный раздела совпадает с величиной своей проекции на эту поверхность.
Изменение кривизны поверхности разделяющей фазы вызывает изменение давления в фазах, определяемое уравнением Лапласа
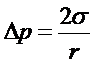(14)
Здесь Dp - избыточное давление, направленное к центру кривизны и называемое капиллярным давлением, или в общем случае
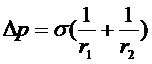(15)
где r1 и r2 - главные радиусы кривизны поверхности.
Изменение термодинамических свойств в реальном переходном слое однокомпонентной системы происходит непрерывно от свойств одной фазы к другой, а в модели Гиббса это приводит к избыткам. В случае многокомпонентной системы происходит процесс перераспределения компонентов между объемом и поверхностью фаз до установления равновесия, приводящее к самопроизвольному снижению межфазного натяжения (свободной энергии). При этом часть компонентов (поверхностно–активных) концентрируются в поверхностном слое (положительная адсорбция Г2>0, 
), а часть уходит из поверхностного слоя (отрицательная адсорбция Г2<0,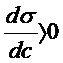 
).
Величину адсорбции выражают двумя способами, как количество вещества в поверхностном слое А, приходящееся на единицу поверхности s (или на единицу массы адсорбента). Это поверхностная концентрация (или емкость монослоя)
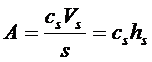(17)
где сs - концентрация адсорбата в поверхностном слое, имеющем объем Vs и толщину hs.
По другому способу выражают величину относительной (избыточной) адсорбции Г как некоторый избыток компонента (адсорбата) в поверхностном слое на единицу поверхности по сравнению с его количеством в равном объеме фазы
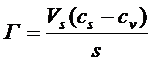(18)
или чаще
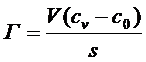(19)
где сv - равновесная концентрация компонента в объеме, с0 - исходная концентрация в том же объеме.
Сравнение (17) и (18) дает
(20)
Очевидно, что если равновесная концентрация после адсорбции мала по сравнению с поверхностной, то абсолютная и относительная адсорбции практически совпадают: Г» A.
Для всех границ раздела фаз жидкость - газ, твердое – газ, твердое – жидкость, жидкость – жидкость справедлив закон действующих масс и равновесие определяется соответствующей константой адсорбционного равновесия, однако существует и некоторое различие.
Так, адсорбцию на границе жидкость – газ можно рассчитать по поверхностной активности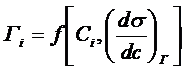 
, используя изотерму Гиббса (9), во всех остальных случаях адсорбция рассчитывается по формуле (19).
Различают мономолекулярную адсорбцию Ленгмюра, описываемую изотермой
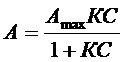(21)
где Аmax - максимальная адсорбция, К - адсорбционная константа, С - концентрация адсорбата. Для определения констант Аmax и К изотерму часто представляют в виде уравнения в линейной форме
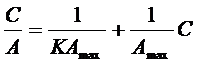(22)
Изотерму адсорбции из растворов на поверхности твердого тела с обменной константой К описывается уравнением (для разбавленных растворов):
(23)
где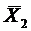 
–молярная доля второго компонента (адсорбата) на поверхности, Х2 – в объеме. Для случая (часто встречающегося) К>>1 и 
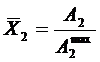(23) переходит в изотерму Ленгмюра (21).
Различают также полимолекулярную адсорбцию газов и паров на твердом адсорбенте, которая описывается изотермой БЭТ:
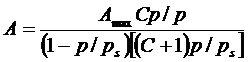(24)
где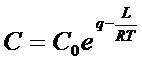 
- константа, в которой q - теплота адсорбции, L - теплота конденсации паров; Ps - давление насыщенных паров; Аmax - ее максимальная величина, соответствующая полному заполнению монослоя (модель Ленгмюра).
Расчет констант Аmax и С осуществляется путем спрямления экспериментальной зависимости 
в координатах линейной формы:
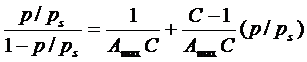(25)
И, наконец, для расчета адсорбции в пористых телах используется изотерма Дубинина – Радушкевича:
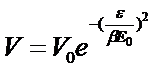(26)
где V - объем адсорбата, поглощенного пористым адсорбентом, V0 – полный объем открытых пор, e - адсорбционный потенциал Поляни, b - коэффициент аффинности, Е0 - характеристическая энергия адсорбции.
К поверхностным явлениям также относятся адгезия, когезия, смачивание и растекание.
Адгезия характеризуется величиной работы адгезии, определяемой по формуле Дюпре:
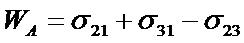(27)
где s21 - поверхностное натяжение твердого тела или жидкости 2 на границе раздела с газом 1, s31 – то же на границе твердого тела 3 с газом 1, s32 - на границе двух конденсированных фаз 2 и 3.
Если одна или две фазы жидкие, то условие равновесия жидкости на поверхности твердого тела или другой жидкости можно характеризовать косинусом краевого угла смачивания по формуле Юнга:
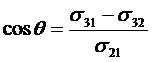(28)
Поскольку нет надежных методов определения поверхностного натяжения на границе раздела твердое – газ, твердое - жидкость, работу адгезии выражают объединенным уравнением Дюпре –Юнга
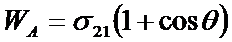(29)
Работа когезии (взаимодействие в однородной фазе) выражается через удвоенное поверхностное натяжение
(30)
Растекание жидкости по поверхности твердого тела или другой жидкости определяется коэффициентом растекания Харкинса
(31)
Если f > 0, нанесенная на поверхность жидкость растекается; если f < 0 - увеличивает первоначальный краевой угол (собирается в каплю).
Поверхностное натяжение зависит от электрического потенциала на границе раздела фаз (ДЭС). Эта зависимость описывается первым и вторым законами Липпмана
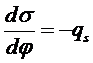(32)
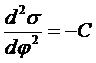(33)
где qs - плотность заряда в ДЭС, С - емкость ДЭС, а j - электрический потенциал. Зависимость поверхностного натяжения от потенциала называют капиллярной кривой.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
1. При конденсации тумана, состоящего из капель кадмия, образовалось 12,5.10-6 м3 жидкого кадмия. Поверхностное натяжение при температуре конденсации равно 570 мДж/м2. Свободная поверхностная энергия всех капель кадмия составляла 53 Дж. Вычислите дисперсность и диаметр капель жидкого кадмия.
РЕШЕНИЕ Энергия Гиббса поверхности определяется по уравнению:
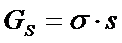
Связь между удельной поверхностью SУД, поверхностью S, объемом V и дисперсностью D выражается соотношением:
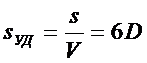
Поверхность капель тумана составляет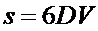 
.
Дисперсность капель кадмия равна
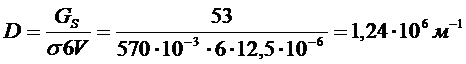
Диаметр капель кадмия равен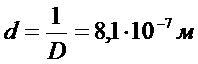 
.
2. Рассчитайте полную поверхностную энергию 10 г. эмульсии гексана в воде с концентрацией 70% мас. и дисперсностью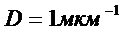 
при температуре 298 К. Плотность гексана при этой температуре 
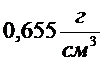, поверхностное натяжение 
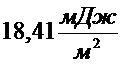, температурный коэффициент поверхностного натяжения 
.
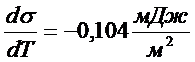РЕШЕНИЕ Полная поверхностная энергия рассчитывается по уравнению Гиббса-Гельмгольца:
.
Поверхность s капель бензола 70% эмульсии массой 10 г составляет:
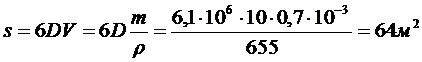
3. Рассчитайте работу адгезии в системе вода-графит, зная, что краевой угол равен 90°, а поверхностное натяжение воды составляет 71,96 мДж/м2. Определите коэффициент растекания воды на графите.
РЕШЕНИЕ Выражение для работы адгезии через краевой угол дается уравнением Дюпре - Юнга:
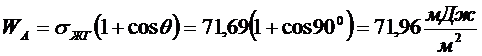
работа когезии.
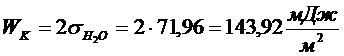
Коэффициент растекания рассчитывается по соотношению:
¦ = WA - WК = 71,96 - 143,92 = -71,96 мДж/м2, т.е. вода не растекается по графиту.
4. Удельная поверхность непористой сажи равна 73,7 м2/кг. Рассчитай площадь, занимаемую молекулой бензола в плотном монослое, исходя из данных об адсорбции бензола на этом адсорбенте при 293 К.
P, Па 1,03 1,29 1,74 2,50 6,67
A·102 , моль/кг 1,57 1,94 2,55 3,51 7,58
Предполагается, что изотерма адсорбции описывается уравнением Ленгмюра.
РЕШЕНИЕ. В линейной форме уравнение Ленгмюра имеет вид
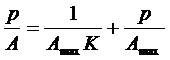
Вначале рассчитывают значения p/А
p/А·10-2, Па·кг/моль 0,656 0,668 0,68 0,712 0,879
p, Па 1,03 1,29 1,74 2,50 6,67
По этим данным строят график в координатах уравнения Ленгмюра в линейной форме (рис. 1).
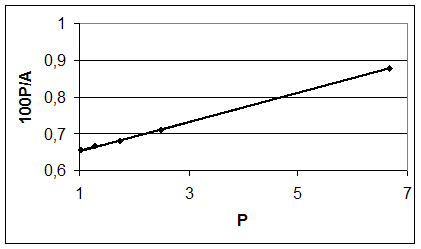
Риc. 1. Изотерма адсорбции бензола в координатах линейной формы уравнения Ленгмюра
Из графика находят:
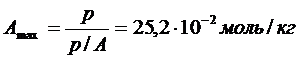
Удельная поверхность адсорбента связана с емкостью слоя Amax соотношением
Площадь, занимаемая молекулой бензола в плотном монослое, равна
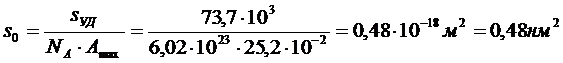
5. Определите адсорбцию азота на двуокиси титана (рутиле) при 75 К при давлении 61·102 Па, если давление насыщенного пара азота при указанной температуре составляет 78,3·103 Па, площадь, занимаемая одной молекулой азота равна 0,16 нм2, удельная поверхность адсорбента – 3,65·104 м2/кг, константа равновесия С = 97,7. Адсорбция носит полимолекулярный характер.
РЕШЕНИЕ. Рассчитаем максимальную адсорбцию азота
По теории БЭТ адсорбция рассчитывается по уравнению:
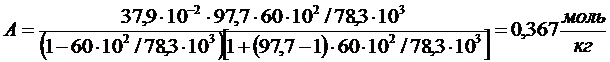
6. Используя константы уравнения Шишковского В=0,173; А=0,046, определите, при какой концентрации поверхностное натяжение водного раствора масляной кислоты при 293К будет равно 6,812·10-2 Н/м. Поверхностное натяжение воды 7,253·10-2 Н/м.
РЕШЕНИЕ Согласно уравнению Шишковского (1.5)
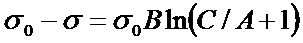
25,5С +1 = 1,423, отсюда С =(1,423-1)/25,5=1,96·10-2 кмоль/м3
7. Вычислите адсорбцию валериановой кислоты на поверхности раздела водного раствора с воздухом при 353К и концентрации С=2,9·10-3 кмоль/м3, если константы уравнения Шишковского в этом случае равны В=0,28; А=0,05 кмоль/м3. Поверхностное натяжение воды составляет 63·10-3Н/м.
РЕШЕНИЕ Константы уравнения Шишковского связаны с константами уравнения Ленгмюра следующим образом:
, 
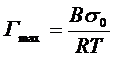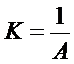
Рассчитываем константы уравнения Ленгмюра
К = 1/0,05 = 20 м3/ кмоль
Рассчитываем адсорбцию по уравнению Ленгмюра
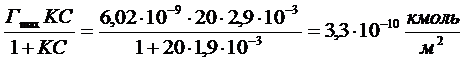
8. Вычислите толщину адсорбционного слоя церотиновой кислоты (С25Н21СООН), адсорбированной из бензольного раствора на поверхности воды. Площадь, занимаемая молекулой ПАВ в насыщенном адсорбционном слое, равна 0,25 нм2, плотность - 0,836 г/см3.
РЕШЕНИЕ. Зная площадь, занимаемую молекулой ПАВ в насыщенном слое, рассчитываем величину предельной адсорбции Гmax:
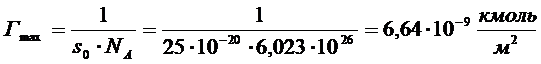
Толщину адсорбционного слоя вычисляем по уравнению:
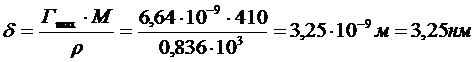
9. Рассчитайте давление паров воды в капилляре радиусом в 1 мкм (краевой угол смачивания примите равным 0). Выразите полученный результат в процентах от нормального значения при t =25 0C.
РЕШЕНИЕ Используя формулу Томсона,получим
; 
; 
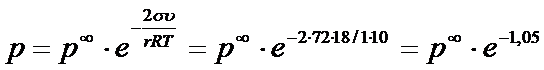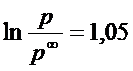10.По приведенным данным рассчитайте (по БЭТ) удельную поверхность адсорбента по изотерме адсорбции бензола на твердой поверхности. Площадь, занимаемая одной молекулой бензола, s0 =49×10-20 м2:
p/ps 0,024 0,05 0,14 0,20 0,265 0,35
А ×103
кмоль/кг 0,0149 0,0348 0.0472 0,0566 0,0663 0,0799
РЕШЕНИЕ. Используя уравнение БЭТ в координатах линейной формы
,
преобразуем данные таблицы для построения их в координатах линейной формы
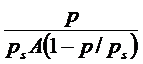1650 1512 3449 4417 5438 6739
0,024 0,05 0,14 0,20 0,265 0,35
после преобразования данных построим зависимость
 |
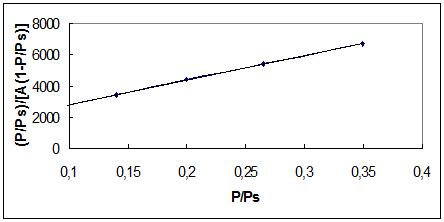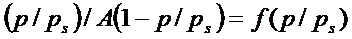
Риc. 2. Изотерма адсорбции бензола в координатах линейной формы уравнения БЭТ.
Получим из графика: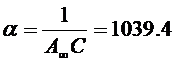 
, 
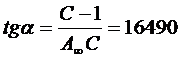, С=16,9, А∞=5,7.10-5 моль/кг.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Суммарная поверхность коллоидного золота, образовавшегося из 5 г Au, составляет 30,6 м2. Определите удельную поверхность частиц, дисперсность и размер частиц гидрозоля, считая их кубическими. Плотность золота 19,6 г/см3.
2. Приняв, что в золе серебра каждая частица представляет собой куб с длиной ребра 40 нм, определите, сколько коллоидных частиц может получиться из 10 г серебра. Плотность Ag 1,05·104 кг/м3.
3. Вычислите удельную поверхность гидрозоля сернистого мышьяка, средний диаметр частиц которого равен 100 нм, а плотность 3,43 г/см3. (Ответ дать в м-1 и в м2/кг).
4. Золь ртути состоит из сферических частиц диаметром 40 нм. Чему равна суммарная поверхность частиц, образующихся из 3 г ртути. Плотность ртути 13,56 кг/м3.
5. Удельная поверхность суспензии селена 15·105 м-1. Определите общую поверхность частиц суспензии, если последнего взято 8 г. Плотность селена 4,28 г/см3.
6. Вычислите удельную поверхность угля, применяемого в топках для пылевидного топлива, если известно, что угольная пыль предварительно просеивается через сито с отверстиями в 50 мкм. Плотность угля 1,8 кг/м3. (Ответ дать в м-1 и в м2/кг).
7. Аэрозоль ртути сконденсировался в виде большой капли объемом 3,0 см3. Определите, на сколько уменьшилась свободная поверхностная энергия ртути, если дисперсность аэрозоля 20 мкм-1. Поверхностное натяжение ртути примите равным 0,415 Дж/м2.
8. Определите энергию Гиббса поверхности 5 г тумана воды, если поверхностное натяжение жидкости составляет 71,96 мДж/м2, а дисперсность частиц - 60 мкм-1. Плотность воды примите равной 0,997 г/см3.
9. Суспензия кварца содержит сферические частицы, причем 30% массы приходится на частицы, имеющие радиус 1·10-5 м, а масса остальных - на частицы радиуса 5·10-5 м. Какова удельная поверхность кварца?
10. Определите свободную энергию 5 г тумана, если поверхностное натяжение равно 73 мН/м, дисперсность частиц 40 мкм-1. Плотность воды 1 г/см3.
11. Рассчитайте полную поверхностную энергию 3 г эмульсии системы "бензол-вода" с концентрацией 45% мас. и дисперсностью 2,5 мкм-1 при температуре 303 К. Примите плотность бензола 861 кг/м3, межфазное поверхностное натяжение 26,32 мДж/м2, температурный коэффициент поверхностного натяжения бензола ds/dT = -0,13 мДж/м2×К.
12. Определите полную поверхностную энергию гептана, если поверхностное натяжение гептана при 0°С равно 22,31 мДж/м2. Температурный коэффициент поверхностного натяжения ds/dT = -0,1мДж/м2 ×К.
13. Определите поверхностное натяжение гептана при 283, 293, 303 К. Примите, что полная энергия не зависит от температуры и для гептана равна 49,6 мДж/м2. Температурный коэффициент поверхностного натяжения ds/dT=-0,1мДж/м2 ×К.
14. Определите поверхностное натяжение бензола при 293 и 323 К, принимая, что полная поверхностная энергия не зависит от температуры и для бензола составляет 61,9 мДж/м2. Температурный коэффициент ds/dT = -0,13 мДж/м2 ×К.
15. Определите краевой угол смачивания, образованный каплей воды на твердом теле, если поверхностные натяжения на границе воздух - твердое тело, жидкость - твердое тело и жидкость-воздух соответственно равны 0,067; 0,020 и 0,074 Дж/м2.
16. Рассчитайте работу адгезии для воды, глицерина и бензола, смачивающих фторопласт. Поверхностное натяжение (на границе с воздухом) воды, глицерина и бензола соответственно равны 71,96; 63,2 и 28,9 мДж/м2, а краевые углы составляют 108, 100 и 46°.
17. Вычислите коэффициент растекания и определите, будет ли растекаться нормальный гексан по воде, если работа когезии для гексана 0,0368 Дж/м2, а работа адгезии гексана к воде 0,0401 Дж/м2.
18. Рассчитайте значение поверхностного натяжения бензола при 293, 313 и 343 К, принимая, что полная поверхностная энергия бензола не зависит от температуры и равна 61,9 мДж/м2. Температурный коэффициент ds/dT = -0,13 мДж/м2 ×К.
19. Краевой угол воды на парафине равен 111° при 298 К. Для 0,1 М раствора бутиламина в воде поверхностное натяжение составляет 56,3 мДж/м2, краевой угол на парафине равен 92°. Рассчитайте поверхностное давление пленки бутиламина, адсорбированного на поверхности парафин - вода. Поверхностное натяжение воды s = 71,96 мДж/м2.
20. Экспериментально получено значение коэффициента растекания гептанола по воде, равное 37 мН/м. Рассчитайте межфазное натяжение на границе вода - гептанол, принимая значения поверхностных натяжений воды и гептанола соответственно 71,96 и 26,1 мН/м.
21. Вычислите поверхностное натяжение олеиновой кислоты, если коэффициент растекания ее по воде равен 24,5 мДж/м2.Поверхностное натяжение воды равно 72,5·10-3 Дж/м2, межфазное натяжение составляет 0,016 Дж/м2.
22. Через водную суспензию, состоящую из частиц кварца и графита, пропускается воздух. Какие частицы будут выносится с пеной, если краевой угол кварца 0°, графита 60°?
23. Порошок кварца и серы осторожно высыпали на поверхность воды. Какое явление можно наблюдать, если краевой угол для кварца 0°, для серы 78°?
24. Рассчитайте работу адгезии глицерина к 14% гелю желатины, нанесенному на парафин, если краевой угол равен 69°. Поверхностное натяжение глицерина s = 63,4 мН/м. Найдите коэффициент растекания глицерина по поверхности геля.
25. Рассчитайте работу когезии вазелинового масла и работу адгезии к гелю желатина, сформированному на фторопласте, если краевой угол равен 40°. Поверхностное натяжение вазелинового масла 30 мДж/м2.
26. Вычислите краевой угол, образованный формамидом на поверхности желатинового геля, если работа адгезии составляет 48,7 мДж/м2. Поверхностное натяжение формамида равно 38,2 мДж/м2.
27. Коэффициент растекания хлорбензола на поверхности воды при 20°С составляет 2,3 мДж/м2. Рассчитайте межфазное натяжение на границе двух жидкостей, принимая значения поверхностного натяжения воды и хлорбензола соответственно 71,96 и 35,97 мДж/м2.
28. Рассчитайте равновесное давление паров над водой, находящейся в капилляре радиусом 1 мкм, предполагая, что угол смачивания равен 0°. Выразите результаты в процентах от давления насыщенного пара при 293 К. Плотность воды 997 кг/м3, поверхностное натяжение 72,75 мДж/м2. Давление насыщенного пара воды при 293 К равно 2338 Па. Что будет, если краевой угол смачивания стенки водой станет равным 90°?
29. Столбик жидкости, помещенный в коническую трубку, самопроизвольно движется к более узкой части, когда он смачивает стенки, и к более широкой части, когда не смачивает. Объясните это явление и укажите, каким законом это определяется, приведите соответствующие формулы.
30. Покажите, чему равна разность h1 - h2 уровней жидкости в двух сообщающихся капиллярах с диаметром d1 и d2. Поверхностное натяжение жидкости равно s. Краевые углы равны нулю. Плотность жидкости равна r.
31. Рассчитайте межфазное натяжение в системе CaF2-вода, зная, что растворимость частиц CaF2 диаметром 0,3 мкм превышает нормальную растворимость (при 293 К) на 18% мас. Плотность частиц CaF2 примите равной 2,5·103 кг/м3.
32. Рассчитайте избыточное давление в капельке воды (за счет кривизны) с удельной поверхностью 3·106 м-1 при температуре 313К, если поверхностное натяжение воды при 298К составляет 71,95 мДж/м2, а температурный коэффициент поверхностного натяжения воды ds/dT = -0,16 мДж/м2 ×К.
33. Рассчитайте равновесное давление паров над капельками воды дисперсностью 2·107 м-1 при температуре 333 К, если поверхностное натяжение воды при температуре 293 К составляет 72,75 мДж/м2, а температурный коэффициент ds/dT= -0,16 мДж/м2 ×К. Давление насыщенных паров воды над плоской поверхностью при 60°С равно 2,058·104 Па, а плотность води 983,2 кг/м3.
34. Во сколько раз изменится кривизна поверхности сферических частиц золя гидроксида кремния, если в результате роста диаметр их увеличится от 10 нм до 100 нм?
35. Определите, при каком пересыщении давление паров над каплей бензола диаметром 2·10-8 м при 313К соответствует равновесному. Поверхностное натяжение бензола 26,13 мДж/м2, а плотность 858 кг/м3. Что будет происходить, если пересыщение паров станет больше или меньше рассчитанной величины?
36. Рассчитайте избыточное давление внутри капелек бензола, равновесных с собственным паром, если удельная поверхность системы составляет 6·108 м-1, а поверхностное натяжение бензола равно 28,87 мДж/м2.
37. При адсорбции полибутадиена из раствора в гексане при температуре 293К на сульфате кальция получены следующие экспериментальные данные:
С, кг/м3 2,0 4,2 6,4 8,0
А·103, кг/кг 2,03 4,216 6,97 7,6
Определите константы уравнения Ленгмюра.
38. При адсорбции углекислого газа на саже с удельной поверхностью 73,7·103 м2/кг были получены следующие данные:
р·10-2, н/м 9,9 49,7 99,8 200
А·102, моль/кг 7,27 15,9 20,67 23,17
Рассчитайте площадь, занимаемую молекулой углекислого газа в плотном монослое, предполагая, что изотерма адсорбции описывается уравнением Ленгмюра.
39. По уравнению Ленгмюра вычислите величину адсорбции азота на цеолите при давлении 1,5·102 н/м2, если Гmax= 38,9·10-3 кг/кг, К = 0,156·10-2.
40. При адсорбции газообразного азота на активном угле при 194,4К были получены следующие данные:
p·10-3, Па 1,86 6,12 17,96 33,65 68,9
А·103, м3/кг 5,06 14,27 23,61 32,56 40,8
Значения А даны для азота при нормальных условиях. Рассчитайте постоянные в уравнении Ленгмюра и удельную поверхность активного угля, принимая плотность газообразного азота равной 1,25 кг/м3, а площадь, занимаемую молекулой азота на поверхности адсорбента, равной 0,16 нм2.
41. По константам уравнения Ленгмюра Гмах = 18,2 кг/кг и К = 0,1·10-2 рассчитайте величину адсорбции углекислого газа на активном угле при давлении газа, равном 4×103 Н/м2,
42. Вычислите константу скорости адсорбции полибутадиена на сульфате кальция из растворов в гексане (концентрация раствора 1%, Т = 293 К) по следующим экспериментальным данным:
t. мин 5 10 15 20 25 45 60 120
А×103. кг/кг 0,9 1,5 2,22 2,5 2,75 3,05 3,1 3,1
43. При адсорбции стеариновой кислоты на сульфате кальция из толуольного раствора различной концентрации получены следующие экспериментальные данные:
С×103 кг/м3 2,5 5,0 7,5 10
А×103 кг/кг 2,0 3,75 5,5 7,5
Определите удельную поверхность адсорбента, если известно, что площадь, занимаемая одной молекулой кислоты в насыщенном монослое, равна 20,5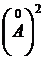 
.
44. Вычислите константу скорости адсорбции лауриндиметилбензиламоний хлорида на силикагеле из водных растворов при 0 0С по следующим экспериментальным данным:
t мин 5 15 30 45 60 120
А×104, кмоль/кг 0,505 0,87 1,37 1,65 1,94 2,01
45. Используя константы эмпирического уравнения Фрейндлиха b =1,5×10-4 и 1/n = 0,32 построить изотерму адсорбции пропионовой кислоты на угле при 290 К в интервале концентраций от 0,03×10-3 кмоль/кг до 0,66×10-3 кмоль/м3.
46. При адсорбции углекислого газа на активированном угле получены следующие данные:
| Равновесное давление Р×10-2, Н/м2 | 10,0 | 44,8 | 100,0 | 144,0 | 250,0 |
| Адсорбция А×103. кг/кг | 32,3 | 66,2 | 96,2 | 117,2 | 145,6 |
Определите константы уравнения Бедекера-Фрейндлиха.
47. Используя уравнение БЭТ, рассчитайте удельную поверхность адсорбента по данным адсорбции азота:
р/рs 0,05 0,15 0,25 0,30
А×103 м3/кг 0,15 0,5 0,8 0,92
Площадь, занимаемая молекулой азота в плотном монослое, равна 0,16 нм2, плотность азота 1,25 кг/м3.
48. При исследовании адсорбции стеариновой кислоты из растворов в н-гексане при различной концентрации С на порошке стали получены результаты:
С×105 моль/л 1 2 4 7 10 15 20 25
А.×103. кг/кг 0,786 0,864 1,0 1,17 1,3 1,47 1,6 1,7
Рассчитайте удельную поверхность порошка стали, принимая площадь молекулы стеариновой кислоты в насыщенном монослое 0,20 нм2.
49. По приведенным данным рассчитайте (по БЭТ) удельную поверхность адсорбента по изотерме адсорбции бензола на твердой поверхности. Площадь, занимаемая одной молекулой бензола s0 = 49×10-2 м2.
р/рs 0,024 0,05 0,14 0,20 0,265 0,35
А×103,
кмоль/кг 0,0149 0,0348 0,0472 0,0566 0,0663 0,0799
50. По приведенным данным рассчитайте (по БЭТ) удельную поверхность адсорбента по изотерме адсорбции бензола, если s0 = 0,49 нм2.
р/рs 0,04 0,05 0,15 0,22 0,27 0,36
А×105 кмоль/кг 3,45 4,53 6,24 7,24 8,05 9,29
51. Величина адсорбции красителя из раствора может быть использована для оценки удельной поверхности порошков. При введении 1 г активного угля в 100 мл раствора метиленового голубого концентрация красителя изменяется от начальной 1.10-4 моль/л до конечной равновесной 6.10-5 моль/л, а при добавлении 2 г угля к такому же исходному раствору равновесная концентрация составила 4×10-5 моль/л. Считая, что адсорбция описывается уравнением Ленгмюра, рассчитайте sуд угля. Площадь, занимаемую молекулой красителя на поверхности, примите равной 0,65 нм2
52. Определите константы уравнения Фрейндлиха для адсорбции бензойной кислоты на угле по следующим данным:
С, кмоль/м3 0,01 0,02 0,03 0,04 0,053
А×103 кмоль/кг 0,5 0,66 0,8 0,93 1,04
53. По изотерме адсорбции бензола определите удельную поверхность адсорбента (Т = 293 К, S0= 49×10-20 м2)
р/рs 0,05 0,12 0,20 0,30 0,40 0,50
А×10 5кмоль/кг 3,1 5,98 8,0 11,0 13,6 17,7
54. При адсорбции из водного раствора ПАВ на гидрофобной поверхности образуется насыщенный адсорбционный слой толщиной 6,25×10-10 м. Рассчитайте молекулярную массу ПАВ, если его плотность 890 кг/м3, а площадь, занимаемая одной молекулой в насыщенном слое, составляет 29,7×10 -20 м2.
55. По экспериментальным данным капиллярной конденсации метанола на силикагеле при 293 К (вариант 1-2) постройте петлю гистерезиса и интегральную кривую распределения объема пор адсорбента по размерам. При указанной температуре молярный объем метанола 40,6×10-6 м3/моль, поверхностное натяжение 22,6×10-3 Н/м, давление насыщенного пара 128.10 2 Па.
p×10 –2 Па 16 32 64 79 96 110 128
А, моль/кг:
адсорбция 2,5 3,5 4,8 6,3 13,0 19,0 22,5
А, моль/кг:
адсорбция 0,8 1,3 1,6 2,2 4,0 3,87
десорбция 0,8 1,3 1,7 3,0 3,7 3,87
56. Полистирол с молекулярной массой 3×105 адсорбируется из толуольного раствора на углеродном адсорбенте (волокне), имеющим удельную поверхность 0,12 м2/кг. Величина предельной адсорбции при образовании монослоя равна 0,033 кг/кг. Рассчитайте площадь, приходящуюся на 1 молекулу полистирола в плотном монослое, и число молекул на поверхности 1 кг адсорбента.
57. При введении ПАВ в синтетический латекс происходит адсорбция молекул на частицах полимера до образования насыщенного монослоя. Определите удельную поверхность и дисперсность частиц полимера по данным адсорбционного титрования, если известно, что в 100 мл латекса с концентрацией полимера 120 кг/м3 введено 2,7×10-4 моля олеата натрия. Учтите, что критическая концентрация мицеллообразования олеата натрия равна 1,2 моль/м3, а площадь, приходящаяся на I молекулу ПАВ в адсорбционном слое при его насыщении составляет 28×10-20 м2 Первоначальное содержание олеата натрия равно 2,8×10-2 моль/кг полимера. Плотность полимера 1050 кг/м3.
58. Измерена адсорбция азота на высокодисперсном порошке. Найдено, что при 77 К степень заполнения поверхности θ = 0,5 достигается при р/рs = 0,02, а при 90 К при p/ps = 0,2. Пользуясь уравнением БЭТ, рассчитайте изостерическую теплоту адсорбции, а также дифференциальные изменения энтропии и свободной энергии адсорбции при 77 К. Теплота испарения жидкого азота при 77 К равна 5,66 кДж/моль.
59. Изотермы адсорбции газов А и В на некотором твердом теле описываются уравнением Ленгмюра. При температуре 77 К заполнение поверхности θ = 0,01 чистым газом А достигается при pА = 1,33.104 Па, а чистым газом В при pB = 1330 Па. Рассчитайте разность теплот адсорбции газов А и В.
60. Используя уравнение Дубинина - Радушкевича, определите общую пористость канальной сажи на основе данных об адсорбции паров бензола. Молярный объем бензола равен 4,06.10-5 м3/моль.
p/ps 0,3 0,4 0,5 0,6
А, моль/кг 1,10 1,38 1,60 1,90
61. При адсорбционном насыщении при 20°С площадь, занимаемая молекулой изобутилового спирта, составляет 0,297 нм2. Вычислите константу В в уравнении Шишковского, если поверхностное натяжение воды равно 72,7 эрг/см2.
62. Определите молекулярную массу адсорбтива, если известно, что при образовании насыщенного адсорбционного слоя ПАВ на границе раствор-газ, площадь, занимаемая 1 молекулой ПАВ, равна 29,7.10-20 м2, толщина адсорбционного слоя ПАВ составляет 6,25.10-10 м и плотность ПАВ равна 890 кг/м3.
63. Известно, что при образовании насыщенного слоя ПАВ на границе раствор-газ площадь, занимаемая молекулой ПАВ, составляет 28 
, толщина адсорбционного слоя - 19,4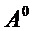 
. Плотность ПАВ 930 кг/м3. Рассчитайте молекулярную массу ПАВ.
64. С помощью сталагмометра получены данные: среднее число капель воды 54,7, среднее число капель исследуемого раствора 88,2. Температура опыта 17,50С, плотность раствора 1,13 г/см3. Поверхностное натяжение воды равно 72,4.10-3 Н/м. Определите поверхностное натяжение раствора.
65. Вычислите длину молекулы стеариновой кислоты (С17Н35СООН), адсорбированной на поверхности воды из раствора в н-гексане. Площадь одной молекулы кислоты в насыщенном монослое 0,20 нм2, плотность кислоты 0,845 г/см3.
66. Для определения поверхностного натяжения воды взвешивают капли, отрывающиеся от капилляра, и измеряют диаметр шейки капли в момент ее отрыва. Оказалось, что масса 318 капель воды равна 5 г, а диаметр шейки капли - 0,7 мм. Рассчитайте поверхностное натяжение воды.
67. Вычислите длину молекулы додецилсульфата натрия, адсорбированного на поверхности воды. Площадь одной молекулы вещества в насыщенном монослое 0,33 нм2, плотность - 0,87 г/см3.
68. Вычислите поверхностное натяжение воды при 13°С по методу счета капель, если диаметр трубки 4,1 мм, а 10 капель воды имеют объем 9,6.10-7 м3. Плотность воды 0,999 г/см3.
69. Рассчитайте величину адсорбции при 17°С для 0,01 кмоль/м3 раствора н-гептиловой кислоты, если поверхностная активность, определенная Ребиндером, равна 
.
70. Вычислите толщину мономолекулярного адсорбционного слоя анилина, если s0 = 0,286 нм2. Молекулярная масса анилина 93, плотность 1,026 г/см3.
71. Для водного раствора пропилового спирта при 295 К найдены следующие значения констант уравнения Шишковского: В = 0,198, А = 0,151. Вычислите поверхностное натяжение раствора при концентрации спирта, равной 0,5 кмоль/м3. Поверхностное натяжение воды равно 72,53 дин/cм.
72. Константы уравнения Шишковского для водного раствора валериановой кислоты при 0°С В = 0,194; К = 10,4. При какой концентрации кислоты поверхностное натяжение раствора будет равно 52,1.10-3 н/м, если σ(H20) = 75,49 дин/см?
73. Для водного раствора пропилового спирта при 293 К найдены следующие константы уравнения Шишковского В = 0,198, А = 0,151. Вычислите поверхностное натяжение раствора и адсорбцию спирта при концентрации, равной 1,0 кмоль/м3. Поверхностное натяжение воды равно 72,53 дин/cм.
74. Определите, при какой концентрации поверхностное натяжение водного раствора масляной кислоты при 293 К будет равно 63,53 дин/см, если константы уравнения Шишковского в этом случае равны В = 0,173, А = 0,046 моль/м3. Поверхностное натяжение воды равно 72,53 мН/м.
75. Вычислите адсорбцию масляной кислоты на поверхности раздела водного раствора с воздухом при 0°С и концентрации С = 0,1 кмоль/м3, если константы уравнения Шишковского в этом случае составляют В = 0,22, А = 0,0165 моль/м3. Поверхностное натяжение воды равно 75,49 мН/м.
76. Вычислите величину адсорбции валериановой кислоты на поверхности водного раствора о воздухом при 80°С и концентрации 2,9.10-3 кмоль/м3, если константы уравнения Шишковского в этом случае равны В = 0,28 и А = 0,05 моль/м3. Поверхностное натяжение воды равно 63 эрг/см2.
77. Вычислите площадь, занимаемую 1 молем ПАВ при образовании насыщенного монослоя, если известно, что молекулярная масса ПАВ равна 97, ρ = 0,93 г/см3, толщина слоя δ= 7,5 А.
78. Определите поверхностную активность масляной кислоты на границе водного раствора с воздухом при 20°С по следующим данным:
С, кмоль/м3 0 0,021 0,05 0,104 0,246
σ, дин/см 72,53 68,12 63,53 58,6 50,3
Рассчитайте адсорбцию при концентрации раствора 0,08 кмоль/м3.
79. Рассчитайте величину адсорбции поверхностно-активного вещества, если поверхностное натяжение на границе раздела изменилось с 75,49 до 55,59 Дж/м2 при концентрации ПАВ 0,5 кмоль/м3 и температуре 293 К. Известно, что константа равновесия К равна 7,73 м3/моль.
80. Поверхностное натяжение жидкости, полностью смачивающей стекло, измеряют, определяя разность высот Dh двух менисков в U –образной трубке. Внутренний радиус узкой части трубки r1 =1,0 мм, а широкой r2 =1,0 см, Dh = 1,9 см, плотность воды при 200С, r = 0,95 г/cм3. Рассчитайте поверхностное натяжение жидкости.
81. Между двумя параллельными пластинами находится слой воды толщиной 0,5 мкм. Рассчитайте давление, сжимающее пластины, если угол смачивания равен q = 0, поверхностное натяжение воды равно 71,96 мДж/м2. Определите силу, которую необходимо приложить для отрыва пластин друг от друга, если размер пластин 10х10 см.
82. Определите равновесное давление паров над каплями воды и бензола радиусом 0,05 мкм при температуре 313 К. Примите, что давление насыщенных паров над плоской поверхностью при этой температуре для воды и бензола рано соответственно 77,6.102 и 24,08.103 Па, мольные объемы 18,1 и 93,4 см3/моль, а значения поверхностного натяжения 69,55 и 26,13 мДж/м2.
83. Оцените размер частиц SrSO4, зная, что их растворимость на 3%(масс) больше растворимости крупных кристаллов. Межфазное натяжение при 298 К примите равным 85 мДж/м2, плотность SrSO4 3,96 г/см2.
