Контрольные задачи к главе I

	— Это всё? — спросила Алиса, стараясь не сердиться. — Держи себя в руках! — сказала Гусеница.
	Л. Кэрролл. Алиса в Стране чудес

ЗАДАЧИ ДЛЯ РЕШЕНИЯ В АУДИТОРИИ

	комбинаторика
1.	В информационно-технологическом управлении банка работают три аналитика, десять программистов и 20 инженеров. Для сверхурочной работы в праздничный день начальник управления должен выделить одного сотрудника. Сколько способов существует у начальника управления?
2.	Начальник службы безопасности банка должен ежедневно расставлять десять охранников по десяти постам. В целях усиления безопасности одна и та же комбинация расстановки охранников по постам не может повторяться чаще одного раза в месяц. Чтобы оценить, возможно ли это, найти число различных комбинаций расстановки охранников.
3.	Сколькими способами можно рассадить 6 человек за круглым столом? (Рассматривается только расположение сидящих относительно друг друга.)
4.	Группа студентов второго курса из 10 человек сдавала зачёт по теории вероятностей. Сколькими способами могли быть проставлены им зачёты?
5.	Между 10 девушками, вышедшими в финал конкурса «Ивановская красавица», разыгрывается три номинации: «Мисс Ивановская красавица», «Вице-мисс» и «Мисс зрительских симпатий». Сколькими способами эти места могут быть распределены?
6.	Отдел рекламы фирмы имеет средства на размещение рекламы только в 15 из 25 городских газет. Сколько существует способов для случайного отбора газет для помещения объявлений?
7.	Сколько различных четырёхзначных чисел можно составить из цифр 1,2,3,4 и 5, если 1) цифры могут повторяться? 2) при условии, что ни одна цифра не повторяется? 3) при условии, что любые две соседние цифры были различны?
8.	Сколько различных «слов» можно получить при перестановке букв в слове «статистика»?
9.	Номер машины состоит из 3 букв и 4 цифр. Сколько всего существует разных номеров, если алфавит содержит 32 буквы?
10.	Сколькими различными вариантами можно распределить 15 студентов на практику на три предприятия, если на первое предприятие идёт 8 студентов, на второе – 5, а на третье – 2.
	определение вероятности
11.	К семинару подготовились 25 студентов из группы, состоящей из 30 человек. Какова вероятность того, что преподаватель спросит не подготовившегося студента?
12.	Игрок сначала бросает белую игральную кость, потом чёрную. Найти вероятность событий: ; ; ; .
13.	Набирая номер телефона, абонент забыл последние две цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.
14.	На первом этаже семиэтажного дома в лифт зашли три человека. Вероятность выхода каждого из лифта на любом этаже одинакова. Найти вероятность событий: ; ; .
15.	Из 40 вопросов, входящих в экзаменационные билеты, студент знает 25. Чтобы получить удовлетворительную оценку студент должен ответить на 2 из трех предлагаемых ему вопросов. Какова вероятность того, что студент получит оценку «удовлетворительно»?
16.	Первенство по баскетболу оспаривают 18 лучших команд, которые путём жеребьёвки распределяются на две группы по 9 команд в каждой, 5 команд обычно занимают первые места. а) Какова вероятность попадания всех лидирующих команд в одну группу? б) Какова вероятность попадания двух лидирующих команд в одну группу и трёх в другую?
17.	В одной счастливой семье было 5 дочерей. Разница в их возрасте составляла один год, однако молодые красавицы скрывали свой возраст. 3-м из них посчастливилось найти своих спутников жизни в одном году. Какова вероятность того, что эти 3 дочери вышли замуж согласно старой традиции по старшинству?
	Геометрическая вероятность
18.	На отрезке длины 20 см помещен меньший отрезок длины 10 см. Найти вероятность того, что точка, наудачу поставленная на больший отрезок, попадет также и на меньший отрезок. Предполагается, что вероятность попадания точки на отрезок пропорциональна его длине и не зависит от его расположения.
19.	Какова вероятность того, что наудачу поставленная в данном круге точка окажется внутри вписанного в него квадрата.
20.	В одной из популярных в Америке игр игрок бросает монету с достаточно большого расстояния на поверхность стола, разграфленную на однодюймовые квадраты. Если монета (3/4 дюйма в диаметре) попадает полностью внутрь квадрата, то игрок получает награду, в противном случае он теряет свою монету. 1) Каковы шансы выиграть при условии, что монета упала на стол? 2) Каковы шансы выиграть при условии, что монета упала на стол и линии имеют толщину в дюйма?

	комбинаторика
1.	На книжной полке стоят 20 книг по алгебре, 12 книг по геометрии, 25 книг по литературе. Сколькими способами можно выбрать книгу по математике?
2.	Маша поссорилась с Петей и не хочет ехать с ним в одном автобусе. От общежития до института с 7 до 8 ч отправляется пять автобусов. Не успевший на последний из этих автобусов опаздывает на лекцию. Сколькими способами Маша и Петя могут доехать до института в разных автобусах и не опоздать на лекцию?
3.	Сколькими способами можно расположить на шахматной доске 8 ладей так, чтобы они не могли взять друг друга?
4.	Абонент забыл две последние цифры 10-значного номера телефона. Сколько вариантов набора номера телефона существует (цифры могут быть одинаковые)?
5.	Группа студентов 2 курса изучает в первом семестре 10 различных дисциплин. Сколькими способами можно составить расписание занятий на 1 сентября, если в этот день предполагается провести 2 занятия, при условии что: а) занятия могут повторяться? б) занятия не могут повторяться?
6.	В лотерее «Спортлото» игрок должен зачеркнуть 6 из 49 возможных чисел от 1 до 49. Сколько существует всех возможных вариантов выбора для игрока?
7.	Сколько четырёхзначных чисел можно составить из цифр 1 и 0?
8.	Сколько различных «слов» можно получить при перестановке букв в слове «статистика»?
9.	Номер на денежной банкноте составляется из 2-х букв и 7 цифр. Найти число таких номеров, используя 33 буквы алфавита.
10.	Для полёта необходимо укомплектовать следующий экипаж космического корабля: командир корабля, первый его помощник, второй помощник, два бортинженера и один врач. Командующая тройка может быть отобрана из числа 25 готовящихся лётчиков, два бортинженера – из числа 20 специалистов, в совершенстве знающих устройство космического корабля, и врач – из числа 8 медиков. Сколькими способами можно укомплектовать экипаж исследовательского корабля?
	определение вероятности
11.	Набирая цифровой код к чемодану, человек не смог вспомнить одну цифру и набрал её наугад. Найти вероятность того, что он угадал.
12.	Брошены две игральные кости. Найти вероятность того, что сумма выпавших очков равна 4.
13.	Абонент забыл шестизначный телефонный номер (первая цифра не 0). Помнит только, что первые две цифры одинаковые, а другие – разные. Найти вероятность того, что он дозвонится с первого раза.
14.	Куб все грани которого окрашены, распилен на 1000 кубиков одинакового размера. Полученные кубики тщательно перемешиваются. Определить вероятность того, что кубик, извлеченный наудачу, будет иметь: 1) одну окрашенную грань; 2) две окрашенные грани; 3) три окрашенные грани.
15.	В студенческой группе 12 девушек и 8 юношей. Случайным образом по списку вызывают 4 человека. Найти вероятность того, что среди вызванных будут: 1) 3 девушки; 2) все девушки; 3) все юноши.
16.	На книжной полке случайным образом расставлены 4 книги по теории вероятности и 3 по статистике. Какова вероятность того, что книги по одному предмету окажутся рядом?
17.	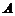и и ещё 8 человек стоят в очереди. Определить вероятность того, что и отделены друг от друга тремя лицами.
	Относительная частота. Статистическая вероятность
18.	Вероятность того, что новый DVD‐проигрыватель в течение года поступит в гарантийный ремонт, равна 0,045. В некотором городе из 1000 проданных DVD‐ проигрывателей в течение года в гарантийную мастерскую поступила 51 штука. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе? НОВАЯ!!
19.	&&&&&
	Геометрическая вероятность
20.	После бури на участке между 40-м и 70-м километрами телефонной линии произошел обрыв провода. Какова вероятность того, что разрыв произошёл между 50-м и 55-м километрами линии?
21.	Какова вероятность того, что наудачу поставленная в данном круге точка окажется внутри вписанного в него правильного треугольника?
22.	Дуэли в городе Осторожности редко кончаются печальным исходом. Дело в том, что каждый дуэлянт прибывает на место встречи в случайный момент времени между 5 и 6 часами утра и, прождав соперника 5 минут, удаляется. В случае же прибытия последнего в эти пять минут дуэль состоится. Какая часть дуэлей действительно заканчивается поединком?