1) 10 класс
| Раздел долгосрочного плана | Содержание раздела долгосрочного плана | Цели обучения |
| 1 четверть | ||
| Повторение курса алгебры7-9 классов | ||
| Функция, ее свойства и график | Функция и способы ее задания. Преобразования графиков функций | 10.4.1.1- знать определениеи способы задания функции; 10.4.1.2- уметь выполнять преобразования графика функции (параллельный перенос, сжатие и растяжение) |
| Свойства функции | 10.4.1.3- уметь определять свойства функции; 10.4.1.4- уметь описывать по заданному графику функции её свойства: 1) область определения функции; 2) область значений функции; 3) нули функции; 4) периодичность функции; 5) промежутки монотонности функции; 6) промежутки знакопостоянства функции; 7) наибольшее и наименьшее значения функции; 8) четность, нечетность функции; 9) ограниченность функции; 10) непрерывность функции; 11) экстремумы функции; | |
| Дробно-линейная функция | 10.4.1.5- определять свойства  дробно-линейной функциии строить ее график; дробно-линейной функциии строить ее график;
| |
| Понятия сложной и обратной функций | 10.4.1.6- знать определение обратной функции и находить функцию, обратную заданной и знать свойство расположения графиков взаимно обратных функций; 10.4.1.7- уметь распознавать сложную функцию f(g(x)) и составлять композицию функций; | |
| Тригонометрические функции | Тригонометрические функции, их свойства и графики | 10.2.3.1- знать определения, свойства тригонометрических функций и уметь строить их графики; |
| Построение графиков тригонометрических функций с помощью преобразований | 10.2.3.2- уметь строить графики тригонометрических функций с помощью преобразований; | |
| Обратные тригонометрические функции | Арксинуса. арккосинуса, арктангенса и арккотангенса | 10.2.3.3- знать определения арксинуса, арккосинуса, арктангенса, арккотангенса и уметь находить их значения; |
| Обратные тригонометрические функции, их свойства и графики | 10.2.3.4- знать определения и свойства обратных тригонометрических функций; 10.2.3.5- строить графики обратных тригонометрических функций; 10.2.3.6- выполнять преобразованиявыражений, содержащих обратные тригонометрические функции; | |
| Простейшиеуравнения, содержащие обратные тригонометрические функции | 10.2.3.7- уметь решатьпростейшие уравнения, содержащие обратные тригонометрические функции; | |
| 2 четверть | ||
| Тригонометрические уравнения | Простейшие тригонометрические уравнения | 10.2.3.8- уметь решать простейшие тригонометрические уравнения; 10.2.3.9- уметь решать тригонометрические уравнения с помощью разложения на множители; |
| Методырешения тригонометрических уравнений и их систем. | 10.2.3.10- уметь решать тригонометрические уравнения, приводимые к квадратному уравнению; 10.2.3.11- уметь решать тригонометрические уравнения с использованием тригонометрических формул; 10.2.3.12- уметь решать однородные тригонометрические уравнения; 10.2.3.13- уметь решать тригонометрическиеуравнения, используя формулы понижения степени тригонометрических функций; 10.2.3.14- уметь решать тригонометрические уравнения методом введения вспомогательного аргумента; 10.2.3.15- уметь решать тригонометрические уравнения с помощью универсальной подстановки; 10.2.3.16- уметь решатьсистемы тригонометрических уравнений; | |
| Тригонометрические неравенства | Решение тригонометрическихнеравенств | 10.2.3.17- уметь решать простейшие тригонометрические неравенства; 10.2.3.18- уметь решать тригонометрические неравенства; |
| Вероятность | Элементы комбинаторики и их применение для нахождения вероятности событий. Бином Ньютона (с натуральным показателем) для приближённых вычислений | 10.3.1.1 - различать понятия: «перестановки», «размещения» и «сочетания» без повторений и с повторениями; 10.3.1.2 - применять формулы для вычисления перестановок, сочетаний, размещений без повторений; 10.3.1.3 - применять формулы для вычисления перестановок, сочетаний, размещений с повторениями; 10.3.1.4 - решать задачи на нахождение вероятностей, применяя формулы комбинаторики; 10.3.1.5 - применять Бином Ньютона для приближённых вычислений (с натуральным показателем); |
| Вероятность события и ее свойства | 10.3.2.1 - знать понятие случайногособытия, виды случайных событий и приводить их примеры; 10.3.2.2 - вычислять вероятность случайных событий, применяя свойства вероятностей; | |
| Условнаявероятность. Правила сложения и умножения вероятностей | 10.3.2.3 - понимать и применять правила сложения вероятностей * P(A + B) = P(A) + P(B) * P(A +B) = P(A) + P(B) – P(A ∙ B); 10.3.2.4 - понимать и применять правила умножения вероятностей * P(A ∙ B) = P(A) ∙ P(B) * P(A ∙ B) = P(A) ∙ PA(B) = P(B) ∙ PB(A); | |
| Формула полной вероятности и формула Байеса | 10.3.2.5 - знать формулу полной вероятности и применять ее при решении задач; 10.3.2.6- знать формулу Байеса и применять ее при решении задач; | |
| Формула Бернулли и ее следствия | 10.3.2.7 - знать условия для применения схемы Бернулли и формулу Бернулли; 10.3.2.8 - использовать формулу Бернулли и ее следствия при решении задач; | |
| Вероятностные модели реальных явлений и процессов | 10.4.2.3, - составлять вероятностные модели реальных явлений и процессов; | |
| 3 четверть | ||
| Многочлены | Многочлены с несколькими переменными и их стандартный вид | 10.2.1.1 - знать определение многочлена с несколькими переменными и приводить его к стандартному виду, определять степень многочлена стандартного вида; |
| Однородные и симметрические многочлены | 10.2.1.2 - уметь распознавать симметрические и однородные многочлены; | |
| Общий вид многочлена с одной переменной | 10.2.1.3- уметь распознавать многочлен с одной переменной и приводить его к стандартному виду; 10.2.1.4 - находить старший коэффициент, степень и свободный член многочлена с одной переменной; | |
| Нахождение корней многочлена с одной переменной методом разложения на множители. | 10.2.1.5 - находить корни многочлена с одной переменной методом разложения его на множители;
10.2.1.6 - использовать формулы
 для разложения многочленов на множители при для разложения многочленов на множители при 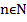 ; ;
| |
| Деление «уголком» многочлена на многочлен | 10.2.1.7- выполнять деление «уголком» многочлена на многочлен; | |
| Теорема Безу, схема Горнера | 10.2.1.8 - применять теорему Безу и ее следствия при решении задач; 10.2.1.9 - применять различные способы нахождения корней симметрических и однородных многочленов; 10.2.1.10 - применять схему Горнера для нахождения корней многочлена; | |
| Метод неопределенных коэффициентов | 10.2.1.13 - знать метод неопределённых коэффициентов и применять его при разложении многочлена на множители; | |
| Теорема о рациональном корне многочлена с целыми коэффициентами | 10.2.1.11 - применять теорему о рациональном корне многочлена с одной переменной с целыми коэффициентами для нахождения его корней; | |
| Уравнения высших степеней, приводимые к виду квадратного уравнения | 10.2.2.1 - применять метод разложение на множители при решении уравнений высших степеней; 10.2.2.2 - применять метод введения новой переменной при решении уравнений высших степеней; | |
| Обобщенная теорема Виета для многочлена третьего порядка) | 10.2.1.12- знать обобщенную теорему Виета и применять ее к многочленам третьего порядка; | |
| Предел функции и непрерывность | Предел функции в точке и на бесконечности | 10.4.1.8- знать определение предела функции в точке и вычислять его; 10.4.1.9 - знать определение предела функции на бесконечности и вычислять его; |
| Асимптоты графика функции | 10.4.1.10 - знать определение асимптоты к графику функции и уметь составлять уравнения асимптот; | |
| Предел числовой последовательности | 10.4.1.11- находить пределы числовыхпоследовательностей, применяя свойства предела функции на бесконечности; | |
| Непрерывность функции в точке и на множестве | 10.4.1.12 - знать определения непрерывности функции в точке и непрерывности функции на множестве; 10.4.1.13 - знать свойства непрерывных функций и применять их при доказательстве непрерывности функции; | |
| Нахождениепределов.Первыйзамечательный предел | 10.4.1.14- применять методы раскрытия неопределенностей вида  и и 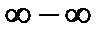 при вычислении пределов;
10.4.1.15- вычислять пределы, применяя первый замечательный предел; при вычислении пределов;
10.4.1.15- вычислять пределы, применяя первый замечательный предел;
| |
| Производная | Определение производной | 10.4.1.16- знать определения приращения аргумента и приращения функции; 10.4.1.17- знать определение производной функции и находить производную функции по определению; 10.4.1.18- находить производные постоянной функции и степенной функции; |
| Понятие дифференциала функции | 10.4.1.19- знать определение дифференциала функции и геометрический смысл дифференциала; 10.4.1.20 - находить дифференциал функции; | |
| Правила нахождения производных | 10.4.1.21 - знать и применять правила дифференцирования; | |
| Производная сложной функции | 10.4.1.22 - находить производную сложной функции; | |
| Производные тригонометрических функций | 10.4.1.23 - находить производные тригонометрических функций; | |
| Производные обратных тригонометрических функций | 10.4.1.24 - находить производные обратных тригонометрических функций; | |
| Физический и геометрический смысл производной | 10.4.2.1 - знать геометрический смысл производной; 10.4.2.2 - знать физический смысл производной; 10.4.3.1 - решать прикладные задачи, опираясь на физический смысл производной; 10.4.3.2 - решать задачи с использованием геометрического смысла производной; | |
| Уравнение касательной к графику функции | 10.4.1.25- составлятьуравнение касательной к графику функции в заданной точке; | |
| 4 четверть | ||
| Применениепроизводной | Признаки возрастания и убывания функции | 10.4.1.26- знать необходимое и достаточное условие возрастания (убывания) функции на интервале; 10.4.1.27- находить промежутки возрастания (убывания)функции; |
| Критические точки и точки экстремума функции | 10.4.1.28- знать определения критических точек и точек экстремума функции, условие существования экстремума функции; 10.4.1.29- находить критические точки и точки экстремума функции; | |
| Точки перегиба функции, выпуклость графика функции. Исследование функции на выпуклость | 10.4.1.30- находить вторую производную функции; 10.4.1.31-знать определение точки перегиба графика функции и необходимое и достаточное условие выпуклости вверх (вниз) графика функции на интервале; 10.4.1.32- уметь находить интервалывыпуклости вверх (вниз) графика функции; | |
| Исследование функции с помощью производной и построение графика | 10.4.1.33- исследовать свойства функции с помощью производной и строить её график; | |
| Наибольшее и наименьшие значения функции на отрезке | 10.4.1.34- находить наибольшее и наименьшее значения функции на отрезке; 10.4.3.3- решать прикладные задачи, связанные с нахождением наибольшего (наименьшего) значения функции; | |
| Случайные величины и их числовые характеристики | Случайные величины | 10.3.2.9 - понимать, что такое случайная величина и приводить примеры случайных величин; |
| Дискретные случайные величины | 10.3.2.10 - знать определение дискретной и непрерывной случайной величины и уметь их различать; 10.3.2.11 - составлять таблицу закона распределения некоторых дискретных случайных величин; | |
| Понятие непрерывной случайной величины | 10.3.2.12 - знать понятие математического ожидания дискретной случайной величины и его свойства; | |
| Числовые характеристики дискретных случайных величин | 10.3.2.13- вычислять математическое ожидание дискретной случайной величины; 10.3.2.14 - вычислять дисперсию и среднее квадратическое (стандартное) отклонение дискретной случайной величины; 10.3.2.15 - решать задачи с использованием числовых характеристик дискретных случайных величин; | |
| Виды распределения дискретных случайных величин. Закон больших чисел | 10.3.2.16 - распознавать виды распределения дискретных случайных величин: биномиальное распределение, геометрическое распределение, гипергеометрическое распределение; 10.3.2.17 - знать формулировку закона больших чисел; | |
| Повторение курса алгебры и начала анализа 10 класса | ||
2) 11 класс
| Раздел долгосрочного плана | Содержание раздела долгосрочного плана | Цели обучения |
| 1 четверть | ||
| Повторение курсаалгебры и начала анализа 10 класса | ||
| Первообразная и интеграл | Первообразная и неопределенный интеграл. Свойства неопределенного интеграла | 11.4.1.1- знать определение первообразной функции и неопределенного интеграла;
11.4.1.2- знать и применять свойства неопределенного интеграла;
11.4.1.3- знать основные неопределенные интегралы:
1. 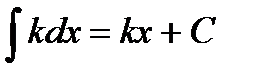 2.
2. 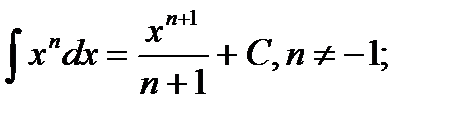 3.
3.  4.
4. 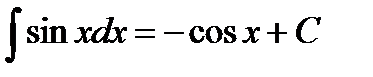 ;
5. ;
5. 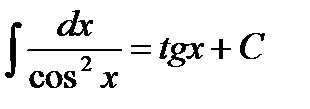 ;
6. ;
6.  , и применять их при решении задач; , и применять их при решении задач;
|
| Методы интегрирования | 11.4.1.4- находитьинтеграл, используя метод замены переменной; 11.4.1.5- находить интеграл, используя метод интегрирования по частям; | |
| Криволинейная трапеция и ее площадь. Определенный интеграл | 11.4.1.6- знать определение криволинейной трапеции и применять формулу Ньютона-Лейбница для нахождения её площади; | |
| Применение определенного интеграла при решении геометрических и физических задач | 11.4.1.7-знать понятие определённого интеграла, уметь вычислять определённый интеграл; 11.4.1.8- вычислять площадь плоской фигуры, ограниченной заданными линиями; 11.4.1.9-знать и применять формулу вычисления объема тела вращения с помощью определенного интеграла; 11.4.2.1- применять определённый интеграл для решения физических задач на вычисление работы и расстояния; | |
| Элементы математической статистики | Генеральная совокупность и выборка | 11.4.2.2-знать и понимать основные термины математической статистики; |
| Дискретные и интервальные вариационные ряды | 11.3.3.1- знать и понимать основные термины математической статистики; 11.3.3.2- обрабатывать выборочные данные для составления дискретных и интервальных вариационных рядов; 11.3.3.3- анализировать данные вариационного ряда в соответствии с заданным условием; | |
| Оценка числовых характеристик случайной величины по выборочным данным | 11.3.3.4- оценивать числовые характеристики случайных величин по выборочным данным. | |
| 2 четверть | ||
| Степени и корни. Степенная функция | Корень n -ой степени и его свойства | 11.2.1.1- знать определение корня n -ойстепени и арифметического корня n -ой степени; 11.2.1.2- знатьсвойства корня п-ой степени; |
| Степень с рациональным показателем. Преобразование выражений, содержащих степень с рациональным показателем | 11.2.1.3- знать определение и свойства степени с рациональным показателем; 11.2.1.4- применять свойства степени с рациональным показателем для преобразования алгебраических выражений; | |
| Преобразование иррациональных выражений | 11.2.1.5- применять свойства корня п-ой степени для преобразования иррациональных выражений; | |
| Степенная функция, ее свойства и график | 11.4.1.10- знать определение степенной функции с действительным показателем; строить график степенной функции с действительным показателем в зависимости от показателя степени; 11.4.1.11- знать свойства степенной функции; | |
| Производнаяи интеграл степенной функции с действительным показателем | 11.4.1.12- знатьи применять правила нахождения производной степенной функции с действительным показателем; 11.4.1.13- знатьи применять правила нахождения интеграластепенной функции с действительным показателем; | |
| Иррациональные уравнения и неравенства | Иррациональные уравнения и их системы | 11.2.2.1- знать определение иррационального уравнения, уметь определять его область допустимых значений; 11.2.2.2- уметь решать иррациональные уравнения методомвозведения обеих частей уравнения в n -ю степень; 11.2.2.3- уметь решать иррациональные уравнения методом замена переменной; 11.2.2.4- уметь решать системы иррациональных уравнений; |
| Иррациональные неравенства | 11.2.2.5- уметьрешатьиррациональныенеравенства; | |
| 3 четверть | ||
| Комплексные числа | Мнимые числа. Определение комплексных чисел | 11.1.1.1 - знать определение комплексного числа и его модуля; 11.1.1.2 - уметь изображать комплексное число на комплексной плоскости; 11.1.1.3- знать определение сопряженных комплексных чисел и их свойства; |
| Действия над комплексными числами в алгебраической форме | 11.1.2.1- выполнять арифметические действия над комплексными числами в алгебраической форме; 11.1.2.2- применять закономерность значения i n при возведении в целую степень комплексного числа в алгебраической форме; 11.1.2.3- уметь извлекать квадратный корень из комплексного числа; | |
| Комплексные корни квадратных уравнений | 11.1.2.4- решать квадратные уравнения на множестве комплексных чисел; | |
| Основная теорема алгебры | 11.1.2.5- знать основную теорему алгебры и её следствия; | |
| Показательная и логарифмическая функции | Показательная функция, ее свойства и график | 11.4.1.14- знать определение показательной функции и строить ее график; 11.4.1.15- применять свойства показательной функции при решении задач; |
| Логарифм числа и его свойства | 11.4.1.16- знать определения логарифма числа, десятичного и натурального логарифмов; 11.4.1.17- знать свойства логарифмов и применять их для преобразования логарифмических выражений; | |
| Логарифмическая функция, ее свойства и график | 11.4.1.18- знать определение логарифмической функции и строить ее график; 11.4.1.19- знать и применять свойства логарифмической функции; | |
| Производная и интеграл показательной функции | 11.4.1.20- находить производную и интеграл показательной функции; | |
| Производнаялогарифмической функции | 11.4.1.21- находить производную логарифмической функции; | |
| Показательные и логарифмические уравнения и неравенства | Показательные уравнения и их системы | 11.2.2.6- знать и применять методы решенияпоказательных уравнений; 11.2.2.7- уметь решать системы показательных уравнений; |
| Логарифмические уравненияи их системы | 11.2.2.8- знать и применять методы решения логарифмических уравнений; 11.2.2.9- уметь решать системы логарифмических уравнений; | |
| Показательные неравенства | 11.2.2.10- уметь решать показательные неравенства и их системы; | |
| Логарифмические неравенства | 11.2.2.11- уметь решать логарифмические неравенства и их системы; | |
| 4 четверть | ||
| Дифференциальные уравнения | Основные сведения о дифференциальных уравнениях | 11.4.1.22- знатьосновные понятия о дифференциальных уравнениях; 11.4.1.23- знать определения частного и общего решений дифференциального уравнения; |
| Дифференциальные уравнения первого порядка c разделяющимися переменными | 11.4.1.24- решать дифференциальные уравнения с разделяющимися переменными; 11.4.3.1- применять дифференциальные уравнения при решении физических задач; | |
| Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами | 11.4.1.25- решать линейные однородные дифференциальные уравнения второго порядка (вида ay''+by'+cy=0,где a,b,c - постоянные); 11.4.3.2- составлять и решать уравнение гармоническогоколебания; | |
| Повторение курса алгебры и начала анализа 10-11 классов | ||




