При решении таких задач используется метод вспомогательных секущих плоскостей, который будет рассмотрен ниже (рис.6.15).
Линия пересечения двух поверхностей в общем виде представляет собой пространственную кривую, которая может распадаться. При пересечении многогранных поверхностей в общем случае получается пространственная ломаная линия.
Обычно линию пересечения двух поверхностей строят по отдельным точкам. Сначала определяют опорные точки в пересечении линий очерков поверхностей. Опорные точки позволяют видеть, в каких пределах расположены проекции линии пересечения и где между ними имеет смысл определять промежуточные точки.
При этом нужно иметь в виду, что проекции линии пересечения фигур всегда располагаются в пределах площади наложения одноименных проекций очерковых линий пересекающихся поверхностей.
Общим способом построения точек линии пересечения двух поверхностей является способ вспомогательных секущих плоскостей или поверхностей. Вспомогательная плоскость или поверхность пересекает данные поверхности по графически простым линиям.
В пересечении этих линий получаются точки, принадлежащие обеим поверхностям, т.е. точки их линии пересечения. В качестве вспомогательных поверхностей обычно используются плоскости или концентрические сферы. (Концентрическими называются сферы, имеющие общий центр и различные радиусы).
Решение позиционных задач основано на применении вспомогательных секущих плоскостей или поверхностей, которые надо выбирать и располагать так, чтобы выполнялось два условия:
1) линии пересечения вспомогательной плоскости или поверхности и заданных поверхностей должны иметь вид прямых линий либо окружностей;
2) вспомогательные плоскости или поверхности располагать так, чтобы проекции линии пересечения были отрезками, прямыми либо окружностями, дугами окружностей.
Рассмотрим общий алгоритм решения:
1) Г i - вспомогательная секущая плоскость или поверхность, i = 1,2,3...n;
2) Г i Ç S i = аi,
G i Ç S 2 = bi - проекции линий пересечения a и b должны быть либо прямые, либо окружности;
3) аi Ç bi = M i Ì m - точки искомой линии пересечения поверхностей.
Все точки линии пересечения поверхностей можно разделить на 3 группы:
1 - габаритные точки каждой из проекций линии пересечения;
{ M } = 2 - точки, определяющие видимость кривой на плоскостях проекций;
3 - случайные или промежуточные точки каждой из проекций.
6.5.1 Применение вспомогательных секущих плоскостей (рис. 6.15).
Задача.
S 1 Ç S 2 = m
S 1 - коническая поверхность вращения
S 2 - сфера.
1) G 1 || P 2; G 1 Î 0, G Î S
2) G 1 Ç S 1 = a1
 (а12 - очерк конуса на P 2)
G 1 Ç S 2 = b1
(b12 - очерк сферы на P 2)
3) а1 Ç b1 ={ 1, 2 }Þ
Þ (точки пересечения
очерков поверхностей на P2 ),
т. 1 и 2 гр.
1) G 2 Î 0, G 2 || P 1
2) G 2 Ç S 1 = а2
Г2 Ç S 2 = b2
3) а2 Ç b2 ={ 3,4 } Þ
точки 1 и 2 группы
1) G i || P 1;
2) G i Ç S 1 = а i
G i Ç S 2 = bi;
3) аi Ç bi ={ 5,6 } Þ
Þ точки 3 группы (а12 - очерк конуса на P 2)
G 1 Ç S 2 = b1
(b12 - очерк сферы на P 2)
3) а1 Ç b1 ={ 1, 2 }Þ
Þ (точки пересечения
очерков поверхностей на P2 ),
т. 1 и 2 гр.
1) G 2 Î 0, G 2 || P 1
2) G 2 Ç S 1 = а2
Г2 Ç S 2 = b2
3) а2 Ç b2 ={ 3,4 } Þ
точки 1 и 2 группы
1) G i || P 1;
2) G i Ç S 1 = а i
G i Ç S 2 = bi;
3) аi Ç bi ={ 5,6 } Þ
Þ точки 3 группы
| 
|
Рисунок 6.15
Опорные точки (пл. Г1) 1 и 2 являются наивысшей и низшей точками линии пересечения, а также точками видимости линий на плоскости П2.
Все промежуточные точки строятся с помощью вспомогательных секущих горизонтальных плоскостей уровня Г i, расположенных равномерно между ними.
Если пересекающиеся поверхности вращения не имеют общей фронтальной плоскости симметрии, то самую высшую и самую низкую точки линии пересечения поверхностей определяют, построив изображения этих поверхностей на плоскость П4, параллельную осевой плоскости.
Вспомогательную плоскость Г2 берем на уровне экватора сферы. Полученные точки 3 и 4 определяют видимость линии пересечения относительно плоскости П1.
Графически простые линии пересечения (окружности) на данных поверхностях получаются от пересечения их горизонтальными плоскостями уровня Г i.
Вводя равномерно между наивысшей и низшей точками линии пересечения вспомогательные секущие плоскости, можно получить достаточное количество промежуточных точек построения линии пересечения.
Горизонтальная проекция линии пересечения строится по принадлежности ее точек конической поверхности.
Аналогично решаются задачи на взаимное пересечение плоскостей и поверхностей вращения из 3 группы позиционных задач (рис. 6.16 а…е).
а) 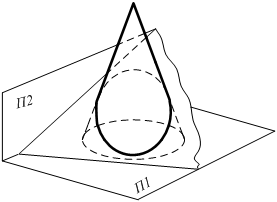 б)
б) 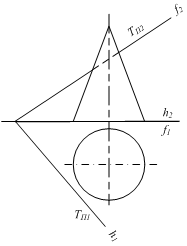
в)  г)
г) 
д)  е)
е) 
Рисунок 6.16




