Пример выполнения практической работы №1

Тема 1. Плоская система сходящихся сил

В строительной практике встречаются случаи, когда необходимо определить внутренние усилия в нескольких стержнях, сходящихся в одной точке. Такое бывает, например, при определении усилии в стержнях ферм. Выполнение данного практического задание помогает освоить приемы определения усилий в стержнях фермы методом вырезания узлов.

Плоская система сил находится в одной плоскости. Силы называются сходящимися, если линии их действия пересекаются в одной точке.

Условия равновесия плоской системы сходящихся сил имеет вид:

∑Fix = 0     сумма проекций всех сил на ось х = 0

∑Fiy = 0     сумма проекций всех сил на ось y = 0

Проекцией силы на ось называется произведение модуля силы на косинус угла между направлением силы и осью. Проекция силы на ось положительна, если направления оси и силы совпадают

 

 

 

F_x = Fcosα

F_y = Fcosβ

Fcos (90°-α) = Fsinα

 

 

В данном случае проекции силы F на ось х и y положительны, поскольку ось направлена слева направо и сила направлена тоже слева направо; ось направлена снизу вверх и сила направлена снизу вверх.

Как выполнить практическую работу №1?

· Внимательно изучить свой вариант задания.

· Действие связей заменить реакциями связей, при этом будем считать, что все стержни растянуты, то есть реакцию связей направляем от узла или точки.

· Выбираем точку, в которой сходятся все заданные силы, включая и реакцию отброшенной связи.

· Задаем систему координат. Оси можно направлять традиционным способом, можно одну из осей направить по направлению отброшенной связи. Непременное условие: оси должны быть перпендикулярны. Выбранную точку помещаем в начало координат

· Составляем уравнение равновесия

∑Fix = 0                         ∑Fiy = 0

· Решаем эти уравнения. Если при решении уравнении получается знак минус, значит усилие направлено в противоположную сторону и стержень сжат.

· Проверяем правильность решения уравнения. Проверка носит математический характер. Это означает, что уравнения решены правильно.

 

Пример выполнения практической работы №1

Задание: определить усилие в стержнях AB и BC, если на эти стержни действуют силы F1=100H и F2 = 200H.

 

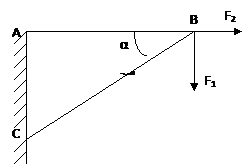
· Заменяем стержни (связи, которые препятствуют перемещению точки B) их реакциями. Реакции направлены вдоль стержней от точки B.

 

Чертеж должен выгладить наглядно. Все силы сходятся в точке B.

· Выбираем систему координат, точку B помещаем в ее начало. Ось х направляем по направлению реакции Rab; ось y перпендикулярно оси x.

 

· Составляем уравнение равновесия.

∑Fix = 0            1)        R_AB – F₂ + R_BC cosα = 0

∑Fiy = 0            2)      – F₁ – R_BC cosβ = 0                       β = 90°- 30° = 60°

 

                     1) R_AB – 200 + R_BC cos30° = 0

2) -100 – R_BC cos60° = 0

Решаем оба уравнения. Из уравнение 2 находим: R_BC = - 100/cos60° = -100/0.5 = -200 (H)

При решении уравнения получили знак минус, значит усилие R_BC направлен в противоположную сторону, стержень сжат.

После этого приступаем к решению уравнения 1.

1) R_AB – 200 – 200cos30° = 0

R_AB = 200 + 200cos 30° = 200(1+cos30°) = 200(1+0.87) = 374 (H) – следовательно, стержень растянут.

Примечание: реакции R_AB и R_BC являются векторами. При решении задачи знак вектора отброшен

· Проверяем правильность решения уравнений. Для этого в одно из уравнений подставляем значение найденных неизвестных.

В 1 уравнение:         R_AB – 200 + R_BC cos30° = 0

                                   374 – 200 + (-200)*0.87 = 374 – 200 – 174 = 0

Уравнения решены правильно.

Ответ: R_AB = 374 H – стержень растянут; R_BC = 200 H – стержень сжат

 

Варианты задания для выполнения практической работы № 1

 

Схемы

F1

1.

                                                                           2.

                                                 

                                                                              

                                                                                                      

 

	4.

3.                                                           F1                       

                                                                                                  F1

                                          F_{2                                                                             F2}

                             

                 

5.

                                             F₁                                                      

                                                                   

                     

α

                               F₂

                                                       

 

                          

Варианты задания для выполнения практической работы № 1

 

Вариант	Схема	α°	β°	F1	F2
1	1	30	30	100	200
2	3	45	70	30	15
3	1	45	45	70	80
4	2	30	-	40	50
5	5	25	-	70	100
6	1	30	45	100	100
7	4	45	-	200	300
8	1	45	35	200	200
9	2	75	-	70	100
10	4	25	-	300	100
11	3	30	30	100	100
12	5	15	-	200	10
13	2	25	-	120	100

      

                   

14	3	30	60	300	200
15	5	80	-	20	100
16	1	25	65	300	100
17	4	30	-	15	15
18	2	60	-	200	15
19	3	30	90	100	20
20	4	35	-	15	120
21	5	20	-	15	15
22	1	60	60	200	100
23	2	15	-	100	70
24	4	30	-	120	90
25	3	35	25	100	120

  

 

 

                                                            

Контрольные вопросы по теме 1

 

1. Назовите способы решения системы двух уравнений.

2. Дать определение понятий: связь, реакция связи.

3. Какие силы называются сходящимися?

4. Проекция силы на ось. Дать определение

5. Условия равновесия плоской системы сходящихся сил.

6. Как должна быть направлена сила, чтобы она сжимала стержень от узла или к узлу?

7. Наиболее часто встречающиеся виды связей. Их реакции