Классификация поверхностей второго порядка

ГЛАВА 6. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА

 

ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА. МЕТОД СЕЧЕНИЙ

Определение 1. По­ верхностью второго порядка называется множество всех точек пространства, координаты которых в какой-либо аффинной системе координат удовлетворяют уравнению второй степени:

, (1)

 где  – действительные числа, причем не все коэф­фициенты при членах второй степени равны нулю.

Рассмотрим основные типы по­верхностей, используя их простейшие (канони­ческие) уравнения. При этом для изучения формы поверхности часто будем прибегать к методу сечений, который применим к любой поверхности. При этом удобно использовать прямоугольную систему координат.

Суть метода сечений состоит в следующем.

Пусть поверхность S задана в прямоугольной системе координат уравнением (1). Пересечем ее плоскостями, параллель­ными координатным плоскостям (или самими координатными пло­скостями), и найдем линии пересечения поверхности с этими пло­скостями. По виду этих линий и выносится суждение о форме по­верхности S.

Определение 2. Поверхность, которая вместе с каждой своей точкой содержит всю окружность, полученную вращением этой точки вокруг некоторой фиксированной прямой d, называется поверхностью вращения.

Прямая d, вокруг которой происходит вращение, называется осью вращения.

Поверхность вращения может быть образована следующим образом:

Пусть в плоскости π дана прямая d и линия γ. Поверхность, образованная вращением линии γ вокруг прямой d есть поверхность вращения с осью вращения d.

 

ЦИЛИНДРИЧЕСКИЕ ПОВЕРХНОСТИ

План:  1. Определение цилиндрических поверхностей.

    2. Классификация цилиндрических поверхностей.

Вопрос

Определение 1. Поверхность, обладающая тем свойством, что вместе с каждой своей точкой М она содержит всю прямую, проходящую через точку М, параллельно данному ненулевому вектору 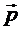, называется цилиндрической поверхностью или цилиндром.

Цилиндрическая поверхность может быть образована следующим образом:

Пусть γ – некоторая линия, а  – ненулевой вектор. Поверхность, образованная всеми прямыми, каждая из которых проходит через некоторую точку линии γ ||  будет цилиндрической.

Эта линия γ называется направляющей поверхности, а параллельные прямые - образующими.

Теорема. Если направляющая цилиндрической поверхности в прямоугольной декартовой системе координат R =(O, ) задана уравнениями

γ: , а образующие || , то эта цилиндрическая поверхность определяется уравнением F (x, y)=0 (*).

Рассмотрим только те цилиндрические поверхности, которые являются поверхностями второго порядка:

Определение 2. Поверхность, которая в некоторой декартовой системе координат задается уравнением , называется эллиптическим цилиндром; поверхность, которая задается уравнением 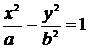, называется гиперболическим цилиндром, а которая задается уравнением  называется параболическим цилиндром.

Для того чтобы построить поверхности, задаваемые этими уравнениями достаточно построить на плоскости   направляющую, уравнение которой на этой плоскости совпадает с уравнением самой поверхности, и затем через точки направляющей провести образующие параллельно оси . Для наглядности следует построить также одно-два сечения плоскостями, параллельными плоскости . В каждом таком сечении получим такую же кривую, как и исходная направляющая.

                  

 

Примечание: Аналогично, если образующие цилиндрической поверхности параллельны другим осям координат, то такая цилиндрическая поверхность задается уравнениями:

1. В плоскости ХО Z:

Направляющая цилиндрической поверхности задана уравнениями

γ: , а образующие || , то эта цилиндрическая поверхность определяется уравнением F (x, z)=0 (*).

2. В плоскости Y О Z:

Направляющая цилиндрической поверхности задана уравнениями

γ: , а образующие || , то эта цилиндрическая поверхность определяется уравнением F (y, z)=0 (*).

 

Вопрос

Пересечем цилиндрическую поверхность плоскостями, непараллельными ее образующим. В сечении получаются различные линии (эллипс, гипербола, парабола). Поэтому цилиндрическая поверхность называется эллиптической, гиперболической, параболической.

Классифицировать цилиндрические поверхности можно на основании вида направляющей. Существует 9 классов цилиндрических поверхностей.

Если прямоугольную декартову систему координат R =(O, ) выбрать так, чтобы образующие цилиндрической поверхности были параллельны вектору , а направляющая линия γ в системе координат R =(O, ) имела каноническое уравнение, то цилиндрическая поверхность определяется следующими уравнениями.

№	Каноническое уравнение	Название	Изображение
1.		Эллиптический цилиндр
2.		Мнимый эллиптический цилиндр	Нет изображения
3.		Пара мнимых плоскостей пересекающихся по действительной прямой (ось OZ)
4.		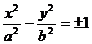Гиперболический цилиндр
5.		Пара плоскостей пересекающихся по OZ
6.		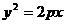Параболический цилиндр
7.		Пара параллельных плоскостей
8.		Пара мнимых параллельных плоскостей	Нет изображения
9.		Пара совпадающих плоскостей по YOZ

КОНИЧЕСКИЕ ПОВЕРХНОСТИ

Определение 1. Конической поверхностью или конусом с вершиной в точке S называется поверхность, которая обладает тем свойством, что вместе с каждой своей точкой М, отличной от точки S, эта поверхность содержит прямую SМ, пересекающую данную в плоскости π линию γ.

Эта линия γ называется направляющей поверхности, а прямые SМ - образующими.

Теорема: Коническая поверхность, направляющая которой в некоторой декартовой системе координат задана уравнением

γ: ,

а вершина совпадает с началом координат, определяется уравнением:    (*), где - действительные числа.

 

Конус

Примечание: Аналогично, если

1) γ: , а вершина совпадает с началом координат, то уравнение конической поверхности: . 

2) γ: , а вершина совпадает с началом координат, то уравнение конической поверхности: . 

Если в уравнении (*) а = в, т.е. γ – окружность, то такая коническая поверхность называется круговым конусом.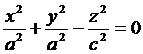

ЭЛЛИПСОИД

Определение 1. Эллипсоидом называется поверхность, которая в некоторой прямоугольно декартовой системе координат задается каноническим уравнением , (1), где  - полуоси эллипсоида.

Если a ≠ b, a ≠ c, b ≠ c, то эллипсоид трехосный.

Исследуем уравнение (1) и определим форму эллипсоида.

1. Точка О (0;0;0) не принадлежит эллипсоиду, так как ее координаты не удовлетворяют уравнению (1).

2. Переменные x, y, z входят в уравнение в четной степени, следовательно, если точка М(x, y, z) принадлежит поверхности, то ей будет принадлежать 7 точек:    М₁ (- x, y, z); М₂ (x, - y, z); М₃ (x, y, - z); М₄ (- x, - y, z);

М₅ (- x, y, - z); М₆ (x, - y, - z); М₇ (- x, - y, - z).

Таким образом, эллипсоид фигура симметричная относительно всех координатных осей, координатных плоскостей, начала координат.

3. Найдем точки пересечения эллипсоида с осями координат:

С осью ОХ: y = z = 0. Из уравнения (1) следует, х² = а², отсюда х = ± а.

              А₁(а; 0; 0), А₂(-а; 0; 0).

С осью ОУ: x = z = 0. Из уравнения (1) следует, у² = b ², отсюда y = ± b.

              В₁(0;, b; 0), В₂(0; - b; 0).

С осью О Z: y = х = 0. Из уравнения (1) следует, z ² = с², отсюда z = ± с.

              С₁(0; 0; с), С₂(0; 0; -с).

Точки А₁(а; 0; 0), А₂(-а; 0; 0), В₁(0;, b; 0), В₂(0; - b; 0). С₁(0; 0; с), С₂(0; 0; -с) – называются вершинами эллипсоида.

    4. Применим метод сечения.

1) Пересечем эллипсоид координатными плоскостями.

Найдем линию пересечения эллипсоида с плоскостью , при этом , и координаты точек эллипсоида на плоскости  удовлетворяют уравнению . Следовательно, линия пересечения является эллипсом с полуосями и .

Сечение плоскостью

 

Аналогично,

сечение в плоскости  дает эллипс , с полуосями  и ;

сечение плоскостью  - эллипс с полуосями и .

 Сечения эллипсоида координатными плоскостями

 

2) Рассмотрим сечение эллипсоида плоскостями, параллельными координатным плоскостям.

2.1) Плоскостью .

Эта плоскость параллельна плоскости и пересекает ось  в точке .

Уравнения этой линии .

а) если , то , получили в левой части первого уравнения неотрицательное число, а в правой – отрицательное, следовательно, уравнение решений не имеет, и точек пересечения нет.

b) если , то  и 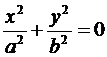, следовательно в сечении получим точки или в зависимости от знака .

с) если , то .

Тогда первое уравнение преобразуем к виду , то есть к виду: ,   где , .

Полученное уравнение является уравнением эллипса.

Сечение плоскостью  является таким же эллипсом, расположенным симметрично первому относительно плоскости .

 

2.2) Плоскостью . Аналогично п. 2.1.

 

2.3) Плоскостью . Аналогично п. 2.1.

                                     

 

Дополнительные сечения эллипсоида                                             Эллипсоид

                    

 

Если в уравнении (1) две полуоси равны друг другу, например, а = b, то эллипсоид называется эллипсоидом вращения. Эллипсоид вращения может быть получен вращением эллипса вокруг одной из осей (например, ОZ).

 

Его уравнение примет вид: .

 

      

 

     Эллипсоид вращения

 

 

ГИПЕРБОЛОИДЫ

План:       1. Однополостный гиперболоид.

                2. Двуполостный гиперболоид.

Вопрос.

Определение 1. Однополостным гиперболоидом называется поверхность, которая в некоторой прямоугольно декартовой системе координат определяется каноническим уравнением: , (1).

Исследуем уравнение (1) и определим форму однополостного гиперболоида.

1. Точка О (0;0;0) не принадлежит однополостному гиперболоиду, так как ее координаты не удовлетворяют уравнению (1).

2. Переменные x, y, z входят в уравнение в четной степени, следовательно, если точка М(x, y, z) принадлежит поверхности, то ей будет принадлежать 7 точек:    М₁ (- x, y, z); М₂ (x, - y, z); М₃ (x, y, - z); М₄ (- x, - y, z);

М₅ (- x, y, - z); М₆ (x, - y, - z); М₇ (- x, - y, - z).

Таким образом, однополостный гиперболоид фигура симметричная относительно всех координатных осей, координатных плоскостей, начала координат.

3. Найдем точки пересечения однополостного гиперболоида с осями координат:

С осью ОХ: y = z = 0. Из уравнения (1) следует, х² = а², отсюда х = ± а.

              А₁(а; 0; 0), А₂(-а; 0; 0).

С осью ОУ: x = z = 0. Из уравнения (1) следует, у² = b ², отсюда y = ± b.

              В₁(0;, b; 0), В₂(0; - b; 0).

С осью О Z: y = х = 0. Из уравнения (1) следует, z ² = - с², следовательно однополостный гиперболоид не пересекает ось О Z. Ось О Z – мнимая ось.

        

 

Применим метод сечения.

1) Пересечем однополостный гиперболоид координатными плоскостями.

Найдем линию пересечения однополостного гиперболоида с плоскостью , при этом , поэтому . Это уравнение на плоскости задает эллипс с полуосями и .

Сечение плоскостью

 

Найдем линию пересечения с плоскостью . На этой плоскости , поэтому 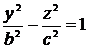. Это уравнение гиперболы на плоскости , где действительная полуось равна , а мнимая полуось равна . 

Сечения однополостного гиперболоида двумя плоскостями                                        

 

Сечение плоскостью  также является гиперболой с уравнением .

2) Рассмотрим сечение однополостного гиперболоида плоскостями, параллельными координатным плоскостям.

2.1) Плоскостью .

Уравнения этих линий .

При любом h, выражение, стоящее в правой части первого уравнения системы, положительно, т.е. . Разделим на него и получим . Это уравнение является уравнением эллипса, подобного эллипсу в плоскости  с полуосями  и .                                                                                          

 

2.2) Плоскостью .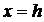

Уравнения этих линий .

При , - в сечении получили пару пересекающихся прямых.

При , - в сечении получается гипербола.

 

2.3) Плоскостью . Аналогично п. 2.2.

 

                             

Изображение однополостного гиперболоида с помощью сечений  Однополостный гиперболоид          

 

 

Если в уравнении (1) , то сечения гиперболоида плоскостями, параллельными плоскости , являются окружностями. В этом случае поверхность называется однополостным гиперболоидом вращения. Его уравнение: .

 

Однополостный гиперболоид вращения

 

Вопрос.

Определение 2. Двуполостным гиперболоидом называется поверхность, каноническое уравнение которой имеет вид:   (2).

Исследуем уравнение (2) и определим форму двуполостного гиперболоида.

1. Точка О (0;0;0) не принадлежит двуполостному гиперболоиду, так как ее координаты не удовлетворяют уравнению (2).

2. Переменные x, y, z входят в уравнение в четной степени, следовательно, если точка М(x, y, z) принадлежит поверхности, то ей будет принадлежать 7 точек:    М₁ (- x, y, z); М₂ (x, - y, z); М₃ (x, y, - z); М₄ (- x, - y, z);

М₅ (- x, y, - z); М₆ (x, - y, - z); М₇ (- x, - y, - z).

Таким образом, двуполостный гиперболоид фигура симметричная относительно всех координатных осей, координатных плоскостей, начала координат.

3. Найдем точки пересечения двуполостного гиперболоида с осями координат:

С осью ОХ: y = z = 0. Из уравнения (2) следует, х² = - а², отсюда следует, что точек пересечения нет.

Аналогично с осью ОУ: x = z = 0. Из уравнения (2) следует, у² = - b ², отсюда следует, что точек пересечения нет.

С осью О Z: y = х = 0. Из уравнения (2) следует, z ² = с², отсюда z = ± с.

Следовательно, двуполостный гиперболоид пересекает ось О Z в двух точках:

С₁(0; 0; с), С₂(0; 0; -с), которые называются вершинами двуполостного гиперболоида.

    4. Применим метод сечения.

1) Пересечем двуполостный гиперболоид координатными плоскостями.

Найдем линию пересечения с плоскостью . На этой плоскости , поэтому . Координаты ни одной точки плоскости   не могут удовлетворять данному уравнению. Следовательно, двуполостный гиперболоид не пересекает эту плоскость.

Найдем линию пересечения с плоскостью . На этой плоскости , поэтому . Это уравнение гиперболы на плоскости , где действительная полуось равна , а мнимая полуось равна .

                  

Сечения двуполостного гиперболоида плоскостью

 

Сечение плоскостью  также является гиперболой, с уравнением .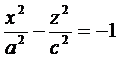

2) Рассмотрим сечение двуполостного гиперболоида плоскостями, параллельными координатным плоскостям.

2.1) Плоскостью .

Уравнения этих линий .

При , , 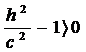разделив на это число, получим каноническое уравнение эллипса.

При , , 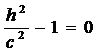то , в сечении получим точку (вершина двуполостного гиперболоида).

При , , правая часть меньше нуля, следовательно, пересечений нет.

2.2) Плоскостью .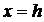

Уравнения этих линий .

При любом значении h правая часть первого уравнения системы отрицательна. Разделим на модуль этого выражения и получим . В сечении получается гипербола с действительной осью OZ.

 

2.3) Плоскостью . Аналогично п. 2.2.

 

                                      

 

Изображение двуполостного                                    Двуполостный гиперболоид

гиперболоида с помощью сечений

 

 

Если в уравнении (3) , то поверхность называется двуполостным гиперболоидом вращения. Его уравнение: .

 

Двуполостный гиперболоид вращения

 

ПАРАБОЛОИДЫ

План:       1. Эллиптический параболоид.

                2. Гиперболический параболоид.

Вопрос 1.

Определение 1. Эллиптическим параболоидом называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид , (1).

Исследуем уравнение (1) и определим форму эллиптического параболоида.

1. Точка О (0;0;0) принадлежит эллиптическому параболоиду, так как ее координаты удовлетворяют уравнению (1).

2. Переменные x, y входят в уравнение в четной степени, следовательно, если точка М(x, y, z) принадлежит поверхности, то ей будут принадлежать и очки: М₁ (- x, y, z); М₂ (x, - y, z); М₃ (- x, - y, z).

Таким образом, эллиптический параболоид фигура симметричная относительно координатной оси О Z, координатных плоскостей XOZ, YOZ.

3. Из уравнения (1) следует, что z ≥ 0, то есть эллиптический параболоид расположен по одну сторону от плоскости XOY.

        

Применим метод сечения.

1) Пересечем эллиптический параболоид координатными плоскостями.

Найдем линию пересечения с плоскостью . На этой плоскости , поэтому .

Координаты только одной точки плоскости  могут удовлетворять данному уравнению, а именно, начала координат.

Найдем линию пересечения с плоскостью . На этой плоскости , поэтому . Это уравнение параболы на плоскости . Сечение плоскостью  также является параболой , симметричной оси ОZ.

2) Рассмотрим сечение эллиптического параболоида плоскостями, параллельными координатным плоскостям.

2.1) Плоскостью .

Уравнения этих линий .

При h > 0, разделив на это число, получим каноническое уравнение эллипса.

При h = 0, , в сечении получим точку О (0,0,0).

При h < 0, правая часть меньше нуля, следовательно, уравнение решений не имеет, и пересечений нет.

 Сечения эллиптического

параболоида координатными плоскостями

2.2) Плоскостью .

Уравнения этих линий .

При любом   h в сечении получили параболу .

2.3) Плоскостью . Аналогично п. 2.2.

                                      

    Дополнительные сечения параболоида                      Эллиптический параболоид                                                           

Вопрос 2.

Определение 2. Гиперболическим параболоидом называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид: 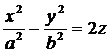  , (2).

Исследуем уравнение (2) и определим форму гиперболического параболоида.

1. Точка О (0;0;0) принадлежит гиперболическому параболоиду, так как ее координаты удовлетворяют уравнению (2).

2. Переменные x, y входят в уравнение в четной степени, следовательно, если точка М(x, y, z) принадлежит поверхности, то ей будут принадлежать и точки: М₁ (- x, y, z); М₂ (x, - y, z); М₃ (- x, - y, z).

Таким образом, гиперболический параболоид фигура симметричная относительно координатной оси О Z, координатных плоскостей XOZ, YOZ.

    3. Применим метод сечения.

1) Пересечем гиперболический параболоид координатными плоскостями.

Найдем линию пересечения с плоскостью . На этой плоскости , поэтому . Это уравнение определяет на плоскости  пару пересекающихся прямых: .

Найдем линию пересечения с плоскостью . На этой плоскости , поэтому . Это уравнение на плоскости задает параболу, ветви которой направлены вниз.

Сечение плоскостью  также является параболой , но ее ветви направлены вверх.

 

Сечения гиперболического параболоида координатными плоскостями

2) Рассмотрим сечение гиперболического параболоида плоскостями, параллельными координатным плоскостям.

2.1) Плоскостью .

Уравнения этих линий .

При h > 0, в сечении получим гиперболу: с действительной осью OX.

При h = 0, , в сечении получим пару пересекающихся прямых: .

При h < 0, в сечении получим гиперболу:  с действительной осью OY.

2.2) Плоскостью .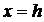

Уравнения этих линий .

При любом h в сечении получим параболу .

2.3) Плоскостью . Аналогично п. 2.2.

                               

Изображение гиперболического

параболоида с помощью сечений                                  Гиперболический параболоид

 

 

КЛАССИФИКАЦИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА

№	Каноническое  уравнение	Название	Изображение
1		Эллиптический цилиндр
2		Мнимый эллиптический цилиндр	Нет изображения
3		Пара мнимых плоскостей пересекающихся по действительной прямой OZ
4		Гиперболический цилиндр
5		Пара плоскостей пересекающихся по OZ
6		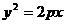Параболический цилиндр
7		Пара параллельных плоскостей
8		Пара мнимых параллельных плоскостей	Нет изображения
9		Пара совпадающих плоскостей по YOZ

 

10		Круговой конус
11		Эллипсоид
12		Эллиптический параболоид
13		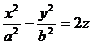Гиперболический параболоид
14		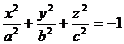Мнимый эллипсоид	Нет изображения
15		Тройка мнимых плоскостей  пересекающихся в точке
16		Однополостный гиперболоид
17		Двуполостный гиперболоид