Расчет прочности по наклонным сечениям

При поперечном изгибе балки вследствие совместного действия поперечной силы и изгибающего момента возникают главные растягивающие и главные сжимающие напряжения:

где σ_x — нормальные напряжения в направлении оси х; σ_у — то же, в направлении у (рис. 4.6, а); τ_ху — касательные напряжения.

Величиной σ_у обычно пренебрегают вследствие ее малости, и формула (4.29) принимает вид

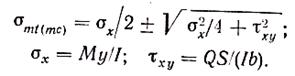
Для балки прямоугольного сечения главные напряжения у нейтральной оси ах=0, тогда

где z=I/S — плечо внутренней пары.

Разрушение может произойти вследствие достижения главными растягивающими напряжениями значения R_bt или главными сжимающими напряжениями R_b. Прочность такого элемента при действии главных сжимающих и главных растягивающих напряжений будет обеспечена при

Эти условия используются в качестве основы для получения зависимостей, оценивающих максимальную и минимальную несущую способность железобетонных элементов по наклонным сечениям.

Поскольку бетон хорошо работает на сжатие, главные сжимающие напряжения опасны главным образом в элементах с тонкой стенкой, коротких консолях и т. п. Более опасны главные растягивающие напряжения. Когда σ_mt достигают прочности бетона при растяжении R_bt, в нем образуется наклонная трещина, которая, развиваясь, разделяет элемент на две части, соединенные между собой бетоном сжатой зоны и арматурой, пересекающей наклонную трещину. При последующем нагружении напряжения в поперечной и продольной арматуре, а также в бетоне над наклонной трещиной возрастают. В большинстве случаев раньше других достигают предельных значений напряжения в поперечной арматуре. При дальнейшем увеличении нагрузки предельных сопротивлений достигают либо напряжения в продольной арматуре, либо в бетоне над наклонной трещиной. В зависимости от этого различают два случая разрушения элемента по наклонным сечениям.

 

Рис. 4.6. Схемы действия главных напряжений (а)

и разрушения изгибаемого элемента по наклонному сечению (б...г)

 

●Случай 1 — при слабой продольной арматуре напряжения в ней, а также в хомутах и отгибах, пересекаемых наклонной трещиной, достигают предела текучести. Происходит взаимный поворот двух частей элемента относительно точки О приложения равнодействующих сжимающих усилий и наступает разрушение бетона (как в нормальных сечениях) (рис. 4.6, б).

●Случай 2 — при наличии достаточно мощной и хорошо заанкеренной продольной растянутой арматуры, препятствующей повороту обеих частей, происходит разрушение бетона над трещиной до достижения текучести продольной арматуры. При этом напряжения в части хомутов и отогнутых стержнях, пересекающих наклонную трещину (рис. 4.6, в), достигают предела текучести.

Разрушение по случаю 1 имеет место, когда прочность наклонного сечения недостаточна при действии изгибающего момента, а по случаю 2 — при действии поперечной силы.

Для обеспечения прочности наклонных сечений изгибаемых элементов расчет должен производиться: а) на сжатие в полосе бетона стенки балки между наклонными трещинами (рис. 4.6, г); б) по наклонной трещине на действие поперечной силы; в) по наклонной трещине на действие изгибающего момента; г) для элементов без поперечной арматуры — из условия, ограничивающего развитие наклонных трещин.

■ Расчет на сжатие в полосе бетона стенки балки между наклонными трещинами. При образовании наклонных трещин бетон между ними испытывает действие главных сжимающих напряжений и одновременно растягивающих усилий от поперечной арматуры (см. рис. 4.6, г), т. е. находится в условиях двухосного напряженного состояния (сжатие — растяжение). Прочность бетона в этом случае будет ниже, чем при одноосном напряженном состоянии. Вследствие этого, а также других факторов для обеспечения прочности бетона на сжатие в полосе между наклонными трещинами (в элементе с поперечной арматурой) должно соблюдаться условие (4.32), полученное с учетом формулы (4.31) и экспериментальных данных:

где φ_ω1 — коэффициент, учитывающий влияние поперечной арматуры, φ_ω1 = 1+5αμ_ω при хомутах, нормальных к оси элемента; α=E_s/E_b; μ_ω=A_sω/(bs); A_sω=A_sωin, A_sωi — площадь сечения одного хомута; n — число хомутов в сечении элемента; s — расстояние между хомутами; φ_b1 = 1—0,01R_b — для тяжелого бетона.

Если условие (4.32) не выполняется, необходимо увеличить размеры сечения или повысить класс бетона.

■ Расчет элементов прямоугольного сечения по наклонной трещине на действие поперечной силы. Наклонная трещина в элементе не образуется (см. формулу (4.31), если σ_mt≤R_bt. Для железобетонных конструкций этому условию соответствует приближенная опытная зависимость

где φ_b3 — коэффициент, для тяжелого бетона φ_b3=0,6.

 

Таким образом, при соблюдении условия (4.33) расчет наклонных сечений по поперечной силе не требуется и арматура может быть назначена по конструктивным соображениям. Если Q > φ_b3R_btbh₀, то прочность сечения нужно обеспечить постановкой поперечной, а иногда и наклонной арматуры в соответствии с расчетом.

 

 

Рис. 4.7. Схема расчетных усилий в наклонном сечении:

а — при расчете на действие поперечной силы;

б — на действие изгибающего момента

 

Для получения расчетных зависимостей рассмотрим схему усилий, действующих в наклонном сечении (рис. 4.7). Для обеспечения прочности наклонного сечения необходимо, чтобы расчетная поперечная сила от внешней нагрузки Q_A не превышала суммы проекций на нормаль к оси элемента расчетных усилий в поперечной арматуре, отогнутых стержнях и бетоне сжатой зоны:

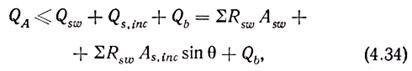
где Q_sw и Q_s,inc — поперечные силы, воспринимаемые хомутами и отгибами, пересекающими наклонное сечение; Q_b — поперечная сила, воспринимаемая бетоном; A_sw и A_s,inc — площади сечения поперечных стержней и отгибов; Ө — угол наклона отгибов к горизонтали; R_sw — расчетное сопротивление хомутов и отогнутых стержней при действии поперечной силы; R_sw=0,8R_s, коэффициент 0,8 учитывает, что в хомутах (отгибах), расположенных у вершины наклонной трещины, напряжения могут быть ниже предельных; значения R_sw приведены в табл. 2.2.

●Расчет хомутов. В практике проектирования наиболее распространено поперечное армирование только хомутами (без отгибов). В этом случае выражение (4.34) примет вид

Поперечная сила, воспринимаемая бетоном над наклонной трещиной, определяется по эмпирической формуле

но принимается не менее φ_b3(1+φ_n)R_btbh₀, где с — длина проекции наклонного сечения, представляющая собой расстояние от вершины наклонной трещины до опоры; φ_b2 и φ_b3 — коэффициенты, для тяжелого бетона φ_b2=2, φ_b3=0,6; φ_n — коэффициент, учитывающий влияние продольных сил от внешних нагрузок и предварительного обжатия [1]; для изгибаемых элементов без предварительного напряжения φ_n=0.

Усилия, воспринимаемые хомутами, заменяются равномерно распределенными усилиями q_sw (рис. 4.7):

тогда

где c₀ — длина проекции наклонного сечения, на которой учитывается работа хомутов. Величина с₀ принимается не более с.

Опыты показывают, что величина с₀ одновременно с ростом с возрастает, но до определенного предела, отвечающего минимуму Q_sw+Q_b. При этом значение c₀ определяют по формуле

и принимают в пределах h₀<c₀<2h₀

При определении расчетной поперечной силы (см. рис. 4.7) нагрузку v, уменьшающую внешнюю поперечную силу, нужно полностью учитывать, лишь когда она безусловно действует (давление воды, грунта и т. п.).

При ее учете

Подставляя (4.36), (4.38) и (4.40) в (4.35) получают

При проверке условия (4.41) задаются рядом наклонных сечений при различных значениях с, не превышающих расстояния от опоры до сечения с максимальным изгибающим моментом, и учитывают наиболее неблагоприятный результат.

Для исключения возможности образования трещин между двумя соседними хомутами необходимо, чтобы поперечная сила воспринималась только бетоном, в этом случае условие (4.36) примет вид с = φ_b2(1 + φ_n)R_btbh /Q. Тогда, приняв c=s и вводя коэффициент 0,75, учитывающий неточности при установке хомутов, получим

В соответствии с нормами [1] расстояние между поперечными стержнями в элементах, не имеющих отогнутой арматуры, в случаях, когда они ставятся по расчету или по конструктивным соображениям, принимают: а) на

приопорных участках (равных при равномерной нагрузке ¹/₄ пролета) для балок h≤450 мм — не более h/2 и не более 150 мм, а для балок h>450 мм — не более h/3 и не более 500 мм; б) на остальной части пролета при h>300 мм — не более 3h/4 и не более 500 мм.

Диаметр поперечной арматуры должен удовлетворять требованиям технологии сварки (см. § 1.2).

 

При проверке, прочности наклонных сечений на действие сжимающих напряжений между наклонными трещинами и на действие поперечной силы вначале проверяют прочность балки на действие наклонных сжимающих усилий по формуле (4.32), затем условие (4.33). Если оно выполняется, то наклонные трещины не образуются, в противном случае требуется производить расчет прочности на действие поперечной силы. В этом случае задаются с≤с_mах= φ_b2h₀/ φ_b3.

Вычислив q_sw по формуле (4.37), находят с₀ по формуле (4.39), принимая ее не более с, 2h₀ и не менее h₀. Подставляя значения с и c₀ в (4.41) проверяют несущую способность.

 

Подбор сечений поперечной арматуры производят методом последовательных приближений. При этом задаются диаметром хомутов из условия сварки с продольной арматурой (см. § 1.2) и шагом хомутов, назначаемым с учетом конструктивных требований и условия (4.42). Далее проверяют условие (4.41) по рассмотренной методике. Если условие (4.41) не выполняется, то изменяют диаметр или шаг хомутов. Блок-схема расчета наклонных сечений на поперечную силу приведена в приложениях.

●Расчет отгибов. Для усиления отдельных частей балки в зонах действия больших поперечных сил (когда Q>Q_sw + Q_b) возможно устройство отгибов путем отвода части рабочей арматуры из растянутой зоны в сжатую (рис. 4.8).

Обычно отгибы устраивают под углом 45° к горизонтали. Наиболее опасным является наклонное сечение, начало которого совпадает с наибольшей ординатой поперечной силы, т. е. у грани опоры. В этом случае, используя (4.34), получают

Для отгибов в каждой последующей плоскости Q_i, принимают равной поперечной силе в сечении, проходящем через низшую точку предыдущего отгиба, т. е.

Начало первого отгиба следует располагать на расстоянии не более 50 мм от грани опоры, а расстояние

в свету между концом последующего и началом предыдущего отгиба должно удовлетворять условию (4.42).

■ Расчет элементов прямоугольного сечения на действие изгибающего момента по наклонной трещине. Расчет наклонных сечений на действие изгибающего момента заключается в проверке их прочности при известном количестве и расположении продольной арматуры, определенных из расчета прочности по нормальным сечениям. Прочность сечения будет обеспечена, если расчетный момент внешних сил М₀ относительно точки О (приложения равнодействующей усилий в сжатой зоне) не превысит суммы моментов расчетных усилий в продольной арматуре, хомутах и отогнутых стержнях относительно той же точки (см. рис. 4.7):

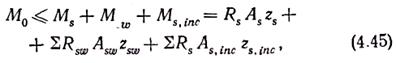
где z_s, z_sw, z_s,inc — расстояния от центров тяжести сечений соответственно продольной арматуры, хомутов и отгибов до моментной точки А. При этом высоту сжатой зоны бетона определяют из условий равновесия проекций усилий в бетоне и арматуре в рассматриваемом сечении на продольную ось элемента. Поскольку напряжение в продольной арматуре у торцов элементов возрастает от нуля у начала стержня до R_s в конце зоны анкеровки (см. § 3.3), вводимое в расчет сопротивление арматуры умножают на коэффициент условий работы, численно равный отношению l_х/1_р.

На действие изгибающего момента рассчитывают наклонные сечения, которые проходят через ослабленные участки элемента: в местах обрыва или отгиба продольной арматуры в пролете, у грани крайней свободной опоры балок и у свободного конца консолей при отсутствии у продольной арматуры специальных анкеров, а также в местах резкого изменения конфигурации элементов.

Рис. 4.8. К расчету отгибов

 

В сечении с наклонной трещиной, пересекающей нормальную ось в центре тяжести сжатой зоны (см. рис. 4.7), прочность, определяемая по формуле (4.45), будет выше, чем полученная из расчета по нормальным сечениям, вследствие включения в работу хомутов и отгибов. Однако это будет только в том случае, когда продольная растянутая арматура, пересекающая наклонную трещину, работает с полным расчетным сопротивлением. Это условие соблюдается при 1_х≥l_an (см. § 1.3) или выполнении специальных мероприятий по анкеровке продольных стержней.

Расчет на действие момента по наклонному сечению в балках с плавно меняющейся высотой может не производиться, если обеспечена: 1) достаточная анкеровка продольной арматуры на свободных опорах элементов (рис. 4.9, а); 2) достаточная анкеровка арматуры, обрываемой в пролете (рис. 4.9, б, в). Анкеровка арматуры на свободных опорах считается обеспеченной при длине заделки рабочей продольной арматуры за внутреннюю грань свободной опоры не менее 5d при Q≤φ_b3(1+φ_n)R_btbh₀ и не менее 10d при Q>φ_b3(l+φ_n)R_btbh₀.

Уменьшение длины заделки возможно, если предусмотреть мероприятия по усилению анкеровки (постановка косвенной арматуры, приварка дополнительных стержней, анкерующих пластин и т. п.).

В целях экономии металла часть продольной арматуры (до 50% максимальной расчетной площади) может не доводиться до опоры и обрываться в пролете там, где она не требуется по расчету. В этом случае растянутые стержни должны заводиться за точку теоретического обрыва (т. е. за сечение 1—1, в котором эти стержни не требуются по расчету) на длину не менее 20d (d — диаметр обрываемого стержня) и не менее l, на протяжении которой в наклонных сечениях (3—3) отсутствие обрываемых стержней компенсируется поперечной арматурой:

где Q, q_sw — расчетная поперечная сила и усилие, воспринимаемое поперечными стержнями в месте теоретического обрыва; 5d — расстояние, на котором обрываемый стержень включается в работу, начиная с сечения 2—2 (рис. 4.9, б).

Места теоретического обрыва стержней устанавливают графоаналитическим способом. С этой целью на эпюру изгибающих моментов от внешней нагрузки (рис. 4.9, в) наносят в том же масштабе эпюру моментов, воспринимаемых сечением элемента с фактически имеющейся растянутой арматурой. Пусть, например, в балке по наибольшему моменту подобрана арматура из четырех стержней 1, 2, 3, 4 (рис. 4.9, б). Два из них 1, 2 доводят до опоры, стержни 3, 4 обрывают в пролете. Для опреде­ления места их теоретического обрыва на графике (рис. 4.9, в) в принятом масштабе откладывают момент, воспринимаемый сечением, армированным стержнями 1, 2. с площадью A_s1,2(M_1,2=R_sA_s1,2z) и проводят горизонтальную линию, параллельную оси. Место пересечения этой линии с эпюрой изгибающих моментов (сечение 1—1) и будет местом теоретического обрыва.

 

 

Рис. 4.9. Обеспечение анкеровки арматуры на опоре (а)

и в пролете (б); построение эпюры арматуры (в):

I — место теоретического обрыва продольных стержней;

II — то же, фактического

■ Расчет элементов без поперечной арматуры. В некоторых типах железобетонных конструкций (сплошных плитах, балках высотой до 15 см, многопустотных сборных плитах высотой h≤30 см и т.п.) допускается не устанавливать поперечную арматуру. В этом случае расчет прочности по наклонным сечениям производят по уравнению (4.34) при Q_sw — Q_s,inc=0.

С учетом опытных данных условия прочности будут иметь вид

но не более 2,5R_btbh₀ и не менее φ_b3(1+φ_n)R_btbh₀, где Q_A — поперечная сила в наклонном сечении; φ_b4 — коэффициент, для тяжелого бетона φ_b4 = 1,5; с — длина проекции наклонного сечения; при расчете задаются рядом значений с≤2,5h₀ с целью определения наиневыгоднейшего.

 

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1. Какие требования предъявляются к конструированию изгибаемых железобетонных элементов (плит, балок)? Назначение продольной и поперечной арматуры.

2. Основные случаи разрушения железобетонной балки по нормальному к ее оси сечению. Условия, определяющие разрушение элемента по сжатой и растянутой зонам; от каких факторов они зависят?

3. Каковы предпосылки, принимаемые для расчета нормальных сечений с одиночной арматурой?

4. Вывод формул для расчета прямоугольных сечений изгибаемых элементов с одиночной арматурой.

5. Каковы особенности расчета переармированных сечений?

6. Чем определяется максимальный и минимальный процент армирования?

7. Как определить несущую способность по нормальному сечению элемента прямоугольного профиля с одиночной арматурой?

8. Как определить площадь сечения продольной арматуры балки при известных М, b, h, R_s, R_b? Как решить эту задачу, если b и h неизвестны?

9. В каких случаях прибегают к установке двойной арматуры?

10. Выведите формулы для расчета прямоугольных сечений изгибаемых элементов с двойной арматурой.

11. Запишите условие, определяющее необходимость установки сжатой арматуры и укажите последовательность ее расчета.

12. Как назначается ширина полки, вводимой в расчет таврового сечения?

13. Напишите условие, при котором тавровое сечение может рассматриваться как прямоугольное.

14. Выведите формулы для расчета таврового сечения.

15. Особенности расчета нормальных сечений элементов, армированных обычной и напрягаемой арматурой в сжатой и растянутой зонах.

16. Каковы причины, вызывающие образо­вание наклонных трещин? Опишите схемы разрушения изгибаемых элементов по наклонным сечениям. 17. Как проверить прочность наклонного сечения изгибаемого элемента при действии сжимающих напряжений?

18. Каково условие образования наклонных трещин? Выведите формулы для расчета хомутов на поперечную силу при наличии трещин.

19. Порядок расчета отгибов при действии поперечной силы.

20. Запишите условия прочности прямоугольного наклонного сечения по изгибающему моменту.

21. Каковы конструктивные требования, обеспечивающие прочность сечений по изгибающему моменту?

22. Как устанавливаются места теоретического обрыва арматуры в пролете и длина заделки стержней l?

23. Каковы особенности расчета элементов без поперечной арматуры?

24. Каковы конструктивные требования к расстановке поперечной арматуры?