Пологие оболочки положительной гауссовой

кривизны на прямоугольном плане

 

Рассматриваемый тип покрытия является одним из наиболее распространенных, поскольку большинство промышленных и общественных зданий имеют прямоугольные планы, а оболочки положительной кривизны наиболее эффективны с точки зрения статической работы.

Покрытие состоит из тонкостенной оболочки переноса или вращения и контурных элементов-диафрагм, передающих нагрузку на колонны или несущие стены. Для покрытий производственных зданий наиболее часто применяют оболочки размерами в плане 18×24 и 18×30 м; для общественных и спортивных зданий диапазон размеров пространственных покрытий значительно шире — от 12×18 до 200 м и более. В нашей стране наибольшие размеры построенных железобетонных покрытий такого типа достигают 100 м (торговый центр в Челябинске — 102×102 м и крытый рынок в Минске — 103×103 м).

Поверхность оболочки может иметь очертание эллиптического параболоида или сферы. Применительно к пологим оболочкам эти поверхности мало отличаются друг от друга. В связи с этим при конструировании обычно применяют сферические оболочки, имеющие постоянную кривизну, обеспечивающую унификацию сборных элементов оболочки. При расчетах же используют поверхность эллиптического параболоида, для которой получаются более простые зависимости. Для сборных оболочек, прямоугольных в плане, рекомендуется также применять часть тороидальной поверхности, имеющую положительную кривизну. Применение такой поверхности позволяет сократить количество типоразмеров сборных плит.

В зависимости от количества и расположения ячеек здания оболочки бывают отдельно стоящими — одноволновыми и многоволновыми. Многоволновые оболочки могут быть неразрезными и разрезными. В неразрезных оболочках приконтурные зоны соседних конструкций жестко связываются между собой и с диафрагмами. Сборные многоволновые оболочки рекомендуется проектировать, как правило, разрезными. Неразрезные оболочки в целом более жесткие, чем разрезные, но требуют большего расхода стали, так как в зоне общего контура перпендикулярно ему возникают растягивающие усилия. Их рекомендуют применять при нагрузках на покрытия, превышающие 6 кН/м², а также в районах с сейсмичностью 7 баллов и более.

Оболочка по контуру опирается на диафрагмы, которые выполняются в виде арок, ферм и контурных брусьев (рис. 13.4). Арки и фермы применяют, как правило, м многоволновых покрытиях, в которых оболочка опирается на четыре угловые точки. В отдельно стоящих оболочках, опертых по периметру здания на ряд часто расположенных колонн или на степы, используют контурный более жесткие в вертикальной плоскости имеют преимущество перед арками. В многоволновых решениях смежные оболочки проектируют на общей диафрагме, а в зоне температурных швов — на спаренных диафрагмах и колоннах.

Толщину и армирование средней зоны гладких монолитных оболочек, где действуют только сжимающие усилия, назначают конструктивно (рис. 13.4, г). Принятую толщину оболочки следует проверять расчетом на устойчивость по формуле (13.9). В приконтурных и угловых зонах оболочку рекомендуется утолщать. При этом в приконтурных зонах укладывают дополнительную рабочую арматуру для воспринятая изгибающих моментов, а в угловых зонах — косую арматуру для воспринятия главных растягивающих усилий.

 

Рис. 13.4. Конструктивные решения пологих сборных оболочек положительной гауссовой кривизны на прямоугольном плане (а...в); схема армирования монолитной оболочки (г):

1 — сборные плиты оболочки; 2 — диафрагма-арка; 3 — выпуски арматуры; 4 — диафрагма-ферма; 5 — контурный брус; 6 — конструктивная арматура; 7 — арматура, рассчитываемая на краевой изгибающий момент; 8 — угловая растянутая арматура

 

Сборные оболочки выполняют из ребристых плит, поверхность которых может быть плоской, цилиндрической или двоякой кривизны. Рекомендуется применять; плоские и цилиндрические плиты (рис. 13.4, а, б), так как плиты двоякой кривизны более сложны в изготовлении. Наиболее распространены плоские плиты размером 3×3; 3×6; 1,5×6 м и цилиндрические размером 3×6 и 3×12 м.

Толщину полки плиты обычно определяют технологическими возможностями завода-изготовителя и принимают 30..35 мм, а при больших пролетах — до 40...50 мм. Плиты проектируют с контурными и поперечными ребрами. Размеры ребер и их армирование назначают расчетом прочности и жесткости при транспортировании, монтаже и проверяют на расчетные нагрузки в стадии эксплуатации. По внешним боковым граням ребер плит предусматривают пазы для образования шпонок, воспринимающих после замоноличивания швов сдвигающие усилия.

Чтобы не вводить дополнительные типы плит в угловых зонах, где возникают растягивающие усилия, устанавливают дополнительную предварительно напряженную или обычную арматуру по верху плит и укладывают монолитного бетона. При этом следует принимать необходимые меры для обеспечения сцепления сборного и монолитного бетона. Поле оболочки армируют сварными сетками, ребра — сварными каркасами с рабочей арматурой класса А-III.

Опыты и расчеты показывают, что в средней части ноля тонких оболочек при равномерно распределенной нагрузке прогибы имеют одинаковое значение (рис. 13.5, а), и если контур не деформируется в своей плоскости, т. е. ω₀=0, то происходит искривление срединной поверхности в приконтурной зоне. Таким образом, в среднем части оболочки имеет место безмоментное состояние, а в приопорной зоне возникают изгибающие моменты. И инженерной практике определение нормальных и сдвигающих усилий для указанного случая производят по безмоментной теории, а изгибающие моменты находятся специальными приемами. Наиболее просто система уравнений (13.3) решается путем введения функции напряжений F(x, у), через которую выражаются усилия:

 

 

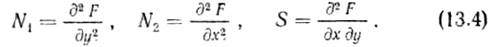
При подстановке (13.4) в (13.3) первые два уравнения обращаются в тождества, а третье принимает вид

Полученное уравнение называют уравнением Пуассона. Решая его одним из известных методов, находят функцию F, а по ней из (13.4) — усилия.

Функция напряжений F(x, у) может быть, например, представлена в виде тригонометрического ряда или полинома. На основе решения в тригонометрических рядах составлены таблицы усилий безмоментного напряженного состояния [9]. Решение уравнения (13.5) в полиномам более наглядно и позволяет получить достаточно простые зависимости для определения усилий N₁ N₂, S [21].

Необходимые для расчета главные усилия, действующие по диагональным сечениям, вычисляют по известной формуле сопротивления материалов

 

N  = (N₁ + N₂)/2 ± .                          (13.6)

 

Для определения возникающих вблизи контура изгибающих моментов существует ряд приближенных приемов [19]. Наиболее часто используют прием, согласно которому реальная оболочка, имеющая, например, сферическую поверхность, у контура заменяется цилиндрической (рис. 13.5, ж). Такая замена является оправданной, так как точный расчет показывает, что изгибающие моменты действуют только в небольшой приконтурной зоне. В этой зоне очертания фактической и заменяющей цилиндрической поверхностей мало отличаются друг or друга. Определение же моментов в цилиндрической оболочке значительно проще. При расчете из нее мысленно вырезают полоску единичной ширины (рис. 13.5, ж). Прогиб такой полоски описывается дифференциальным уравнением:

w₁=Dw,                                       (13.7)

аналогичным уравнению равновесия балки на упругом основании (роль реакций упругого основания выполняют усилия N). В уравнении (13.7) D — цилиндрическая жесткость, w — перемещения в направлении внутренней нормали к поверхности оболочки. Решения (13.7) хорошо изучены, табулированы [24] и позволяют легко находить значения моментов.

В качестве примера покажем усилия, возникающие в отдельной квадратной оболочке (a = b, r₁=r₂ = r) под действием равномерно распределенной нагрузки. Полагая диафрагму абсолютно податливой из своей плоскости и абсолютно жесткой в своей плоскости (вертикальном направлении), будем иметь граничные условия при х = ±а, y = ±b, N₁ = N₂ = 0.

Полученные для этого случая усилия N₁, N₂, S, N_max, N_min и их значения показаны на рис. 13.5, б...е. Из рис.

Pис. 13.5. К расчету пологих оболочек положительной

гауссовой кривизны на прямоугольном плане:

I – зона безмоментного напряженного состояния в оболочке; II — то же, моментного; 1 — область двухосного сжатия; 2 — область сжатия в одном направлении, растяжения — в другом

 

13.5, д, е видно, что почти во всей оболочке имеет место область двухосного сжатия и лишь в угловых частях возникает сжатие в одном направлении и растяжение в другом. На рис. 13.5, и показана эпюра моментов при шарнирном опирании оболочки. В этом случае наибольший изгибающий момент будет иметь место в сечении, находящемся на расстоянии х = 0,597  от края оболочки (при r = 40 м, h = 0,07 м, x≈1,0 м):

М_max = 0,0937rhq.                              (13 8)

По этим усилиям и подбирают арматуру, устанавливаемую в нижней зоне.

При проектировании сборных оболочек во многих случаях оказывается достаточным ограничиться рассмотренным инженерным расчетом в стадии эксплуатации (не прибегая к более точным машинным методам), тем более, что определяющими при подборе сечений оказываются усилия, возникающие при транспортировании и монтаже элементов оболочки.

Помимо расчета прочности для исключения потери устойчивости толщина гладкой оболочки должна удовлетворять условию

h≥ ,                                     (13.9)

где Е_b — начальный модуль упругости бетона оболочки.

Диафрагму рассчитывают на нагрузку от собственного веса и сдвигающих усилий S, передающихся с оболочки (рис. 13.5, з). Если диафрагмой является ферма, то в усилия S приводятся к узловым нагрузкам, при этом следует учитывать эксцентричное приложение сдвигающих сил относительно оси верхнего пояса фермы. Определение продольных усилий в элементах ферм производится по общим правилам. Арочные диафрагмы в конструктивном отношении подобны двухшарнирным аркам. В средней части арка диафрагмы под воздействием касательных усилий работает на внецентренное растяжение, на приопорных участках — на внецентренное сжатие [9].

В контурных брусьях, опертых на ряды колонн, помимо растягивающих усилий действуют изгибающие моменты, по характеру аналогичные моментам в неразрезных балках. Арматуру в контурном брусе рассчитывают на внецентренное растяжение и размещают по контуру сечения бруса. Ее рекомендуется выполнять предварительно напряженной. Для улучшения передачи сдвигающих усилий с оболочек на диафрагмы на верхнем поясе последних устраивают выступы для образования шпонок.

 

Купола

 

●Куполом называют пространственную конструкцию, состоящую из гладкой или ребристой оболочки с вертикальной осью вращения и растянутого опорного кольца. При наличии фонарного проема в вершине купола устраивают сжатое фонарное кольцо.

Купола применяют для покрытий круглых и много-угольных в плане зданий (зрелищно-спортивных и выставочных залов, планетариев, резервуаров и др.) пролетом до 200 м. Форма купола обычно определяется архитектурными, технологическими и другими требованиями. В связи с этим принимают оболочки купола сферические (образованные вращением дуги круга), конические, глиптические, многогранные. Конические купола уступают сферическим и эллиптическим по технико-экономическим показателям, но более просты в возведении; применяют их при пролетах до 30 м. В последнее время используют также купола, образованные волнистыми или складчатыми элементами.

Стрела подъема f тонкостенных куполов может изменяться в широких пределах от 1/2 D до 1/10 D. Наиболее экономичными являются купола с f = 1/3...1/5 D.

Опорное кольцо, воспринимающее распор купола, может лежать на сплошном основании, образованном степами, или на отдельных колоннах.

По способу возведения купола делят на монолитные и сборные. Монолитные купола проектируют гладкими, сборные — из ребристых цилиндрических или плоских панелей трапециевидного очертания в плане. Монолитные купола возводят на сплошной опалубке, повторяющей геометрию купола. Такой способ возведения сложен, трудоемок и требует больших затрат на опалубку. Поэтому в строительстве применяются преимущественно сборные купола.

Разрезка куполов на сборные элементы может быть радиальной и радиально-кольцевой. Радиальную разрезку (рис. 13.6, а) применяют для куполов диаметром примерно до 40 м. В этом случае криволинейные элементы (рис. 13.6, б) понизу опирают на возведенное ранее опорное кольцо, вверху - на фонарное, которое во время монтажа поддерживается лесами; после его окончания леса снимают. Сопряжение сборных элементов оболочки с нижним и верхним кольцами осуществляют на сварке соединительных пластин с закладными деталями. Сборные элементы окаймлены по контуру ребрами, размеры которых и армирование (плоскими каркасами) устанавливают расчетом прочности и жесткости на нагрузки, возникающие при перевозке и монтаже, а также на устойчивость купола при эксплуатации. Для обеспечения поля оболочки минимальной толщины (30...40 мм) устраивают поперечные ребра через 2...3 и, рассчитываемые на полную расчетную нагрузку на купол.

Радиально-кольцевая разрезка (рис. 13.6, б) может применяться и в куполах диаметром более 40 м. Сборные элементы, имеющие в плане форму трапеции (рис. 13.6. г), в этом случае могут быть как плоскими, так и криволинейными. Первые проще в изготовлении, однако ухудшают работу конструкции под нагрузкой, поскольку в местах стыков плит будут переломы, а этот приводит к возникновению в оболочке нежелательных изгибающих моментов.

После окончания монтажа швы между сборными элементами замоноличивают бетоном, а выпуски арматуры и закладные детали сваривают между собой (рис. 13.6, д).

 

Рис. 13.6. Конструкции сборных куполов:

1 — сборный элемент оболочки; 5 — опорное кольцо; 3 — фонарное кольцо;

4 — монтажная стойка; 5 — закладные детали; 6 — соединительные стержни; 7 — бетон омоноличивания

 

Опорное кольцо купола может быть сборным или монолитным. Для повышения трещиностойкости и жесткости кольцо устраивают предварительно напряженным. В этом случае для создания предварительного натяжения высокопрочную арматурную проволоку класса В-II наматывают по периметру кольца с последующим бетонированием. Предварительное натяжение арматуры осуществляют также с помощью канатов или стержней, располагаемых в пазах по периметру кольца и закрепляемых в специально устроенных выступах. Для купольных покрытий диаметром не более 30 м при устройстве на уровне опорного кольца горизонтального покрытия, опоясывающего купол по всему периметру, целесообразно передавать распор на это покрытие. Покрытие в этом случае проектируют с учетом передающихся на него распора и изгибающих моментов. Если нижнее кольцо купила диаметром более 30 м укладывается на жесткие стены, то под кольцом устраивают цилиндрические катки или шарниры скольжения, обеспечивающие радиальное перемещение опорного кольца.

Армирование гладких монолитных оболочек куполов при толщине до 70 мм можно выполнять конструктивно, одиночной сеткой из стержней диаметром 4...6 мм, шагом 150...200 мм. При большей толщине рекомендуется устанавливать две сетки. В зоне примыкания оболочки к кольцу толщину оболочки увеличивают и ставят дополнительную меридиональную арматуру из стержней диаметром 6...8 мм, рассчитанную по опорному изгибающему моменту, а также кольцевую арматуру для воспринятия растягивающих усилий.

В куполе, при действии нагрузки, изменяющейся по произвольному закону, возникают меридиональные, кольцевые усилия, изгибающие моменты, сдвигающие, поперечные силы и другие внутренние усилия, для определения которых нужно исходить из общих уравнений теории тонкостенных оболочек. Если же купол нагружен осесимметричной нагрузкой, имеет гладкую поверхность без изломов, толщина оболочки мала, а конструкция опор обеспечивает свободные радиальное и угловое смещение, то внутренние изгибающие, крутящие моменты и поперечные силы не возникают и расчет куполов может производиться по безмоментной теории. Поскольку в реальных конструкциях оболочка защемлена в опорном муре, в ней возникают опорные изгибающие моменты, быстро затухающие. Эти моменты вычисляются методами строительной механики.

Определим усилия в куполе по безмоментной теории. Элемент купола (рис. 13.7, а), ограниченный двумя меридиональными и кольцевыми сечениями, находится под воздействием меридионального, кольцевого усилия и внешней нагрузки. При осесимметричной нагрузке сдвигающие усилия S = 0 и усилия N₁ и N₂ могут быть определены из условий статики. Сделаем горизонтальный разрез (рис. 13.7, б). Сумму вертикальных сил на части купола выше сечения, заданного углом φ, обозначим через Q_φ. Тогда, проектируя все силы на ось z, получим

Q_φ = N₁ sinφ·2πа,

где а=r₂sinφ; r₂ — радиус кривизны в плоскости, перпендикулярной меридиональной (r₁ — радиус кривизны в меридиональной плоскости, см. рис. 13.7, б). Отсюда

N₁ = Q_φ/(2πa·sinφ).                                 (13.10)

Горизонтальная проекция этого усилия Н, называемая распором:

Н = N₁ cosφ = Q_φ ctgφ/(2πa).                       (13.11)

 

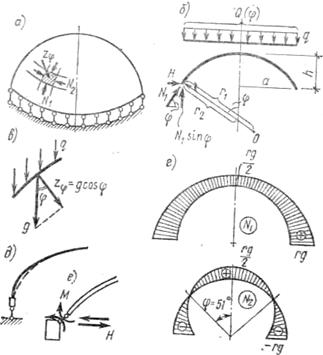
Рис. 13.7. К определению усилий в куполе

 

Растягивающее усилие в кольце от действия распора:

U = На = Q_φ ctg/(2π).                              (13.12)

По этому усилию подбирают рабочую арматуру кольца.

Величину кольцевого усилия N₂ можно получить, спроектировав на нормаль все силы, действующие на элемент поверхности. Тогда будем иметь

N₁/r₁ + N₂/r₂ = z_φ,                                   (13.13)

где z_φ — проекция нагрузки на нормаль к поверхности. В качестве примера расчета рассмотрим усилия, возникающие в сферическом куполе (r=r₁=r₂) от собственной массы. В этом случае Q_φ=A_φg, z_φ =gcosφ (рис. 13.7, в), где g — вес купола на единицу поверхности; A_φ — площадь поверхности сферического купола, A_φ = 2πrh, h=r(1-соsφ), a = rsinφ. Тогда, используя формулы (13.10) и (13.13), найдем

N₁ = 2πr² (1-cosφ) g/(2πr sin²φ) = rg/(1+cosφ),

N₂ = z_φr — N₁ = gr cosφ — rg/(l + соsφ).                  (13.14)

Для полусферического купола усилия (рис. 13.7, г) составят при φ = 0° N₁=rg/2, N₂=rg/2; при φ=90° N₁=rg, N₂ = — rg.

Из рис. 13.7, г видно, что при φ = 51°49' усилие N₂ изменяет знак, и в нижней части купола в кольцевом направлении возникают растягивающие напряжения. Учитывая это обстоятельство, в сборных куполах из тонко-стенных ребристых плит нежелательно проектировать оболочки с половиной центрального угла φ>51°49' из-за сложности воспринятая растягивающих усилий в элементах нижней части оболочки.

Распор купола с учетом (13.11) и (13.14)

H_φ = rg cosφ/(1 + соsφ),                            (13.15)

и растягивающее усилие в опорном кольце

U = H_φ0a = r²gsin2φ₀/[2(l+соsφ₀)].                       (13.16)

Из последней формулы видно, что при φ₀ = 90° U = 0. Учитывая это, для уменьшения усилия в опорном кольце в приопорной зоне устраивают переходную кривую, изменяя очертание купола (рис. 13.7, д).

Kак отмечалось выше, у места сопряжения оболочки с опорным кольцом в ней возникают изгибающие моменты M и горизонтальный распор Н (рис. 13.7, е). Их определяют методами строительной механики из условия равенства нулю взаимного угла поворота и взаимного опия сечений в примыкании оболочки к кольцу от суммарного воздействия всех сил:

а₁₁М + а₁₂Н + а₁₀ = 0,

a₂₁М + а₂₂Н + а₂₀ = 0,                                (13.17)

где а₁₁, а₁₂, а₁₀ — взаимные углы поворота в рассматриваемом сечении от действия М = Н = 1 и g; a₂₁, а₂₂ и а₂₀ — взаимное горизонтальное смещение сечений от этих же усилий,

а₁₁ = s,    а₁₂ = s² sinφ₀/2,

а₂₂ = s³ sin²φ₀/2,    s = 0,76 .                          (13.18)

 

Смещения сферической оболочки а₁₀ и а₂₀ при действии нагрузки от собственного веса определяют по формулам [23]

а₁₀ = 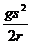 sinφ₀.

а₂₀ = (cosφ₀ + 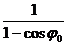)sinφ₀,                        (13.19)

По полученным усилиям производят расчет прочности и трещиностойкости сечений купола. Расчет несущей способности сферических куполов на осесимметричную нагрузку может производиться по методу предельного равновесия [9].

 

Гипары

 

●Гипары (гиперболические параболоиды) состоят из оболочки и диафрагм и могут применяться как самостоятельные конструкции (рис. 13.8, б) или в качестве элемента составных оболочек (см. рис. 13.2, з).

Оболочки таких покрытий при прямоугольном плане могут быть образованы двумя способами: а) переносом образующей параболы, выпуклой вверх (вниз) по направляющей параболе, выпуклой вниз (вверх) (см. рис. 13.1, г); скручиванием прямоугольника или параллелограмма, края которых остаются прямыми (рис. 13.8, а). Ими перекрываются общественные, производственные, складские и другие здания с размером плана 10...70 м и более. Гипары находят в последние годы все более широкое распространение благодаря ряду достоинств, к которым относятся: линейчатость поверхности, Позволяющая упростить устройство опалубки, заготовку арматуры (так как стержни прямолинейные), облегчить отделку поверхности; небольшое количество типоразмеров элементов в сборных оболочках; высокая устойчивость; хороший водосток; архитектурная выразительность. Основным недостатком является наличие значительных растягивающих усилий в одном из направлений.

Покрытия могут быть выполнены в виде одного гипара (рис. 13.8, б) или составными — из нескольких гипаров (см. рис. 13.2, д). По способу возведения они могут быть сборными и монолитными. Монолитные оболочки чаще всего гладкие. Плиты сборных оболочек по краям обычно окаймлены ребрами, геометрические размеры и армирование которых определяются нагрузками при монтаже. Для воспринятия сдвигающих усилий при бетонировании стыков сборных плит предусматривают шпонки.

Членение на сборные элементы целесообразно выполнять вертикальными плоскостями, параллельными сторонам контура.

Гипары обычно проектируют с контурными балками или фермами. Возможно также применение контурных брусьев по рядам колонн и опирание на сплошные стены. В сильно искривленных отдельных гипарах пролетом ≤30 м утолщения оболочки по контуру могут не устраиваться. В покрытиях из составных гипаров по линиям сопряжения отдельных лепестков устраивают коньковые балки. Монтаж сборных гипаров, как и других оболочек двоякой кривизны, ведут с помощью стальных подмостей или кондукторов.

Армирование оболочки определяют усилиями, действующими в ней от внешней нагрузки. Рекомендуется располагать арматуру по прямолинейным образующим и направляющим (рис. 13.8, б). Для армирования плит следует использовать сварные сетки. При больших растягивающих усилиях целесообразно применять предварительно напряженные стержни. Нижние углы могут быть усилены косыми стержнями, служащими для восприня­тия главных растягивающих напряжений.

Рис. 13.8. Гипары:

1 — основная арматура; 2 — растянутая арматура угловых зон; 3 — затяжка

 

Расчет по безмоментной теории оболочек, показанных на рис. 13.1, г, аналогичен расчету оболочек положительной кривизны на прямоугольном плане. Нужно лишь иметь в виду, что кривизна в направлении оси х отрицательна, поэтому усилия N₁ будут растягивающими и должны полностью восприниматься рабочей арматурой. Усилия N₂ сжимающие.

Для поверхности, показанной на рис. 13.8, а, решение уравнения (13.5) будет

и при граничных условиях N₁ = 0 при x=±b; N₂ = 0 пря y=±а (абсолютная податливость контурных элементов, из своей плоскости),

Из (13.21) видно, что N₁ и N₂ равны нулю не только на контуре оболочки, но и во всей ее области. Касательные усилия постоянны по сечению и имеют направление, обратное первоначально принятому. Таким образом, при равномерной нагрузке, как и в седловидной оболочке, имеет место растяжение в направлении парабол, обращенных выпуклостью вниз, и сжатие в направлении парабол, обращенных выпуклостью вверх. Для часто встречающегося на практике случая а = b из (13.6) получают главные усилия

N_max = N_min = - S = qa²/(2f).                          (13.22)

Расчет гипаров по моментной теории даже в упругой постановке представляет значительные трудности и про­изводится на ЭВМ с применением численных методов [9]. Определение полной несущей способности гипаров при равномерно распределенной нагрузке может быть произведено методом предельного равновесия [9].

Касательные силы с оболочки передаются на контурные конструкции. Если таковыми будут жесткие стены, то они в состоянии воспринять касательные силы; если фермы, то в нижних углах возникает распор H₁, для воспринятия которого могут быть устроены затяжки (рис. 13.8, б) или контрфорсы.

 

Цилиндрические оболочки

 

●Цилиндрическими оболочками называют тонкостенные покрытия, состоящие из тонкой криволинейной плиты (собственно оболочки), бортовых элементов и поперечных диафрагм (рис. 13.9).

Цилиндрические оболочки бывают однопролетными и многопролетными (рис. 13.9, в), одноволновыми и многоволновыми (рис. 13.9, б). В зависимости от характера работы под нагрузкой оболочки условно разделяют на длинные, отношение пролета которых l₁ к длине волны l₂ более 4, средней длины при 1<l₁/l₂<4, и короткие при l₁/l₂≤1. Первые два вида обычно объединяют одним наименованием — длинные оболочки. Применяемые на практике длинные оболочки обычно имеют размеры: l₁ = 24; 30; 36 м; l₂=12 м, короткие l₁ = 12 м, l₂ = 24; 30 м.1

Рис. 13.9. Кострукции длинных (а...ж) и коротких (з, и)

цилиндрических оболочек:

1 – оболочка; 2 – бортовой элемент; 3 — диафрагма; 4 — моменты одноволновой и 5 – многоволновой оболочки; 6 — напрягаемая арматура; 7 — конструктивная арматура поля оболочки; 8 – арматура, рассчитываемая на краевой момент; 9 – угловая растянутая арматура; 10 — сборные плиты оболочки

 

■ Длинные цилиндрические оболочки. Высоту оболочки h, включающую сечение бортового элемента, рекомендуется принимать (1/10...1/15)l₁, стрелу подъема f = (1/6...1/8)l₂, а высоту бортовых элементов (1/20...1/30)l₁ (рис. 13.9, а). Оболочки бывают монолитные (гладкие) и сборные ребристые, получившие более широкое распространение вследствие своей индустриальности. Очертание плит оболочки может быть круговым, эллиптическим и т. п. Наиболее простым и удобным для сборных плит является круговое очертание.

Бортовые элементы, в которых размещается основная растянутая арматура, существенно уменьшают вертикальные и горизонтальные смещения краев оболочки. Это видно из рис. 13.9, г, на котором показаны усилия и перемещения в поперечном сечении оболочки при отсутствии и наличии бортовых элементов. Для сборных конструкций обычно применяют предварительно напряженные бортовые элементы.

Опорные диафрагмы выполняют в виде арок с затяжками или балок переменной высоты, опирающихся на колонны или стены.

Возведение сборных цилиндрических оболочек осуществляют в двух основных вариантах.

●В первом варианте предварительно напряженные бортовые элементы пролетом l₁ устанавливают на проектной отметке, а для уменьшения монтажных усилий под них подводят 2...3 временные опоры. По верху бортовых элементов укладывают сборные криволинейные ребристые панели размером 3×12 м (рис. 13.9, б). Далее производят сварку выпусков арматуры плит и бортового элемента и замоноличивание швов. После того как бетон затвердеет, временные опоры убирают и оболочка работает как пространственная конструкция. С целью экономии материалов и устройства водостока бортовые элементы могут выполняться переменной высоты с некоторым увеличением подъема конструкции и средней части пролета.

●Во втором варианте ребристые плиты оболочки размером 3×6 м (рис. 13.9, е) бетонируют на заводе с бортовыми элементами. Далее на лесах все элементы объединяют в единую систему с помощью предварительно напряженной арматуры, пропускаемой через специальные каналы, устраиваемые в бортовых элементах. После сварки стыков, замоноличивания швов и инъекции каналов раствором леса убирают.

Первый вариант по расходу материалов менее экономичен, что связано с условиями работы сборных элементов на монтаже и наличием стыков элементов оболочки с бортовыми элементами, однако он не требует устройства лесов и проведения на строительной площадке ответственных работ по натяжению арматуры и инъецированию раствора.

Все элементы оболочки должны быть рассчитаны на усилия, возникающие при изготовлении, монтаже, а также эксплуатации готового сооружения. Конструкция стыков зависит от вида передаваемых через них усилий. В средней части сборных оболочек в нормальных сечениях действуют сжимающие и небольшие сдвигающие усилия. Стыки здесь решаются путем замоноличивания швов бетоном и устройства шпонок. В местах соедине­ния оболочки с бортовыми элементами и диафрагмами действуют значительные сдвигающие усилия и изгибающие моменты. Их воспринимают шпонками и сваркой выпусков арматуры. В угловых зонах для воспринятая главных растягивающих напряжений смежные элементы соединяют сваркой выпусков арматуры или накладками через закладные детали. Принципиальная схема армирования монолитной цилиндрической оболочки показана на рис. 13.9, ж. В неразрезных многопролетных оболочках кроме растянутой арматуры в пролете ставится арматура в верхней части оболочки для воспринятия растягивающих напряжений над опорой (диафрагмой).

Как уже указывалось, железобетонные оболочки, подобно другим железобетонным конструкциям, в начальной стадии нагружения работают упруго, после образования трещин в бетоне растянутой зоны в них развиваются пластические деформации и с увеличением нагрузки происходит разрушение. В соответствии с этим статический расчет оболочек производится по упругой стадии и по стадии предельного равновесия (т. е. по стадии разрушения).

Точный расчет оболочки в упругой стадии математики труден. Для практических расчетов разработаны методы, основанные на допущениях, применяемых к определенным конструктивным решениям. Широкое применение нашли методы, основанные на работах В. 3. Власова, в которых оболочка заменяется вписанной в нее складкой [9]. Эти методы позволяют рассчитывать упругие оболочки по прочности, жесткости и трещиностойкости при различных нагрузках.

Вместе с тем исследования показали, что длинные цилиндрические оболочки с жестким контуром могут рассчитываться по прочности раздельно в продольном я поперечном направлениях. Расчет в продольном направлении может быть произведен по методу предельного равновесия как балки с криволинейным поперечным: сечением, а расчет в поперечном направлении на сдвигающие усилия и изгибающие моменты производят из условия равновесия элементарной полосы оболочки, вырезанной по ее длине. Таким методом могут быть рассчитаны одноволновые и многоволновые цилиндрические оболочки, не подкрепленные в пролете поперечными ребрами, при l₁/l₂≥3 для крайних и l₁/l₂≥2 для средних волн, а также оболочки l₁/l₂≥1, у которых в пролете предусматривается устройство не менее трех поперечный ребер высотой h≥l₂/25 при действии симметричной равномерно распределенной нагрузки.

Рассмотрим расчет длинной однопролетной цилиндрической оболочки кругового симметричного профиля на действие вертикальной нагрузки по методу предельного равновесия. Расчет ведется по III стадии напряженно-деформированного состояния как балки криволинейного сечения. Напряжения в бетоне сжатой зоны равны R_b, а в растянутой арматуре — Rs. Схема усилий в поперечном сечении показана на рис. 13.10, а. Очевидно, прочность оболочки в продольном направлении будет обеспечена при условии

M₁ ≤ M_u,                                            (13.23)

где M₁ — максимальный момент в середине пролета оболочки от действующей нагрузки; М_u — момент внутренних сил, действующих в сечении в предельном состоянии относительно центра круговой части сечения,

где hrdθ-площадь элементарного участка сечения оболочки длиной rdθ и толщиной h; θ_p — половина центрального угла сжатой зоны.

Положение границы сжатой зоны определяют из условия равенства нулю проекций всех действующих в сечении сил на горизонтальную ось ∑х=0:

2  R_b hrdθ = 2R_b θ_p rh = R_sA_s.                       (13.26)

При проверке несущей способности из уравнения (13.26) находят θ_p и подставляют его в (13.25).

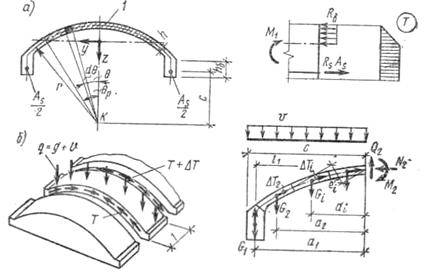
Рис. 13.10. К расчету длинной цилиндрической оболочки в

продольном (а) и поперечном (б) направлениях: 1 — сжатая зона

 

Если при заданном моменте и размерах поперечного сечения оболочки требуется найти площадь арматуры A_s, то в уравнении (13.23) полагают M_u = M₁, далее подставляют в уравнение (13.25) значение R_sA_s из (13.26) и, произведя преобразования, получают выражение для определения θ_p:

sin θ_p — cθ_p/r — M/(2R_b hr²) = 0.                     (13.27)

Подставляя найденное значение θ_p в (13.26), находят сечение арматуры

A_s = 2R_bθ_prh/R_s.

Для определения поперечных изгибающих моментов в гладкой оболочке вырежем из оболочки полосу единичной ширины (рис. 13.10, б). Полоса будет находиться под действием внешней вертикальной нагрузки v, веса оболочки g и касательных сил Т и Т+ΔТ, действующих по плоскостям разреза. Очевидно,

здесь ΔQ — приращение поперечной силы на рассматриваемом участке; S — статический момент поперечного сечения оболочки.

Действующий в полосе поперечный момент определяют из условия равновесия (рис. 13.10, б)

где М₀ — момент от внешней нагрузки и собственной массы,

G_i — нагрузка от веса i-ro участка оболочки; М_ΔT — изгибающий момент от сдвигающих сил относительно рассматриваемого сечения

Значения поперечных изгибающих моментов могут определяться по таблицам [9]. Вид эпюры поперечных изгибающих моментов в одноволновых оболочках см. на рис. 13.9, г.

Расчет диафрагм длинных цилиндрических оболочек производят на усилия от собственного веса и сдвигающие усилия, передающиеся с оболочки, аналогично расчету диафрагм оболочек положительной гауссовой кривизны на прямоугольном плане.

■ Короткие цилиндрические оболочки. Эти оболочки бывают монолитные и сборные (см. рис. 13.9, з, и). Наиболее часто применяют оболочки с шагом диафрагм 6...12 м при отношении l₁/l₂≤0,5 и стреле подъема f≥(1/7)l₂. Такие оболочки рассчитывают упрощенным методом, выполняя раздельно расчет плиты, бортового элемента и диафрагмы.

Толщину плиты монолитной оболочки (см. рис. 13.9, з), нагруженной собственным весом, весом кровли и снега, принимают по производственным соображениям без расчета равной 5 см при l₁ = 6 м, 7...9 см при l₁ = 12 м. Бортовой элемент назначают высотой h₁ = (1/10...1/15)l₁, шириной b₁ = (1/5...1/2)h₁.

При соотношении пролетов 0,5≤l₁/l₂<l, тяжелых и сосредоточенных нагрузках короткие оболочки рассчитываются методом перемещений с учетом поперечных деформаций контура [9]. Оболочки пролетом l₁≤12 м при l₁/l₂<0,5 при равномерной нагрузке допускается рассчитывать приближенным методом. В этом случае армирование плиты назначают конструктивно (сеткой из стержней диаметром 5...6 мм шагом 10...15 см), а для бортовых элементов и диафрагм выполняется расчет. При расчете принимают, что бортовые элементы являются частью оболочки и работают совместно с ней. Оболочку рассчитывают как балку криволинейного сечения пролетом l₁, шириной l₂, опирающуюся на диафрагмы. В середине пролета однопролетной одноволновой оболочки изгибающий момент

Тогда площадь поперечного сечения продольной растянутой арматуры в бортовых элементах будет

где z — плечо внутренней пары, по данным испытаний z=0,55(f+h₁).

Продольную арматуру бортовых элементов объединяют в сварные каркасы, поперечные стержни которых ставятся конструктивно. Вблизи бортовых элементов оболочку армируют дополнительными сетками, а над диафрагмой также ставят дополнительную сетку, которую заводят на длину 0,1 l ₁ в каждую сторону от диафрагмы.

Как и в длинных оболочках, малая толщина сводчатой плиты обусловливает передачу на диафрагмы нагрузок, действующих на плиту главным образом за счет сил S, направленных по касательной к срединной поверхности оболочки. Расчет диафрагмы в этом случае производят с учетом взаимодействия с плитой оболочки. Для средней диафрагмы в многопролетных оболочках и расчет вводится плита оболочки шириной, равной шагу диафрагм, для крайних диафрагм — шириной l₁/2.

Сборные короткие оболочки состоят из плоских ребристых плит и диафрагм в виде ферм (см. рис. 13.9, и), валок, арок. Совместная их работа обеспечивается устройством бетонных шипов на верхнем поясе диафрагм, пазов на наружных гранях продольных и торцовых ребер плит, установкой арматурных каркасов в швах замоноличивания. Расчет коротких сборных оболочек производится в соответствии с двумя этапами работы конструкции: до и после замоноличивания швов между сборными элементами покрытия. До замоноличивания швов сборные элементы рассчитывают как разрезные конструкции на действие нагрузок, возникающих при изготовлении, транспортировании и монтаже. После замоноличивания швов (в стадии эксплуатации) оболочку рассчитывают на действие постоянных и временных нагрузок как пространственную конструкцию по схемам разрушения, охватывающим одну или две крайние плиты согласно [9].

 

Висячие оболочки

 

В последние годы для покрытий больших пролетов в сооружениях промышленного, культурно-бытового и общественного назначения (цехи, склады, кинотеатры, крытые рынки) широко применяют висячие оболочки.

●Висячие железобетонные оболочки состоят из совместно работающих вант, железобетонного покрытия (собственно оболочки) и опорной конструкции (рис. 13.11). Основные несущие элементы в висячих оболочках—ванты, работающие только на растяжение, что позволяет полностью использовать в работе высокопрочную сталь и добиваться ее минимального расхода. Высокая несущая способность, простота изготовления и монтажа, возможность возведения в короткие сроки обусловливает высокую эффективность висячих оболочек, особенно в покрытиях большепролетных сооружений. При пролетах более 100 м они экономичнее железобетонных оболочек других типов.

Однако покрытиям со свободно подвешенными вантами присуща высокая деформативность, их геометрическая форма существенно зависит от вида внешней нагрузки. Чтобы обеспечить стабильность геометрической формы покрытия, а также повысить его жесткость и трещиностойкость, железобетонные висячие оболочки выполняют с предварительным напряжением, которое осуществляют одним из следующих способов:

●после монтажа вант и укладки железобетонных кровельных плит ванты приводятся в напряженное состояние с помощью пригрузов (временной нагрузкой или вертикальными оттяжками); после замоноличивания швов и выдержки бетона пригрузы снимают и железобетонная плита (оболочка) обжимается;

●после монтажа вант, укладки кровельных плит, аамоноличивания швов и выдержки бетона ванты натягивают домкратами на жесткую несущую контурную конструкцию. В этом случае ванты размещают в специальных каналах, заполняемых раствором после окончания натяжения;

●после монтажа вант и укладки кровельных плит швы между ними заполняют раствором на напрягающем цементе. Ширина швов назначается из условия создания в оболочке заданного напряжения.

При небольших пролетах для повышения неизменяемости покрытия и снижения местных деформаций применяют жесткие нити, состоящие из прокатных и сварных балок.

По конфигурации в плане и взаимному расположению вант висячие оболочки бывают с параллельными (рис. 13.11, а), радиальными (рис. 13.11, б, в), перекрестно расположенными и полигональными вантами.

●Систему с параллельно расположенными вантами применяют при прямоугольном плане. Такая конструкция менее эффективна вследствие трудности воспринятия распора, величина которого весьма значительна. Обычно распор воспринимается анкерами, жесткими рамами, а при небольших пролетах — контурными балками, работающими на изгиб (рис. 13.11, г...е).

●Висячие оболочки с радиальным расположением вант применяют при круглом плане здания. Эти оболочки состоят из вант, наружного сжатого и внутреннего растянутого кольца и выполняются по двум схемам (рис. 13.11, б, в). Покрытия такой формы наиболее выгодны, поскольку позволяют максимально унифицировать все элементы оболочки и обеспечивают безмомент-ную работу наружного опорного кольца.

●Висячие оболочки с перекрестной сеткой из вант применяют для зданий овального, эллиптического или прямоугольного очертания в плане. Сетка обычно устраивается ортогональная, пологая. Перекрестные вантовые сетки имеют очертание поверхности положительной или отрицательной гауссовой кривизны.

При выборе системы вант следует иметь в виду, что по расходу арматуры на оболочку в целом, а также по расходу бетона на опорный контур оболочки с радиальной системой вант примерно в 1,5 раза экономичнее оболочек, имеющих перекрестную систему из вант.

Висячие железобетонные оболочки, как правило, проектируют пологими с провесом f = (1/10...1/30)l.

Рис. 13.11. Конструктивные решения висячих железобетонных оболочек:

1 — сборные плиты; 2 — ванты; 3 — опорное кольцо;

4 — контурная балка; 5 - рама; 6 — анкер; 7 — бетон шва

 

Для изготовления вант используют стержневую горячекатаную арматуру классов А-III, A-IV, A-V, стальные канаты, а также арматурные пучки из высокопрочной проволоки. Стальные канаты для устранения неупругих деформаций подвергают предварительной вытяжке усилием, равным 65 % разрывного.

Опорный контур и краевые элементы выполняют из сборного или сборно-монолитного бетона высоких классов. Для облегчения сборных элементов опорного контура они могут предусматриваться корытообразного сечения. Полость стальных или железобетонных корытообразных элементов заполняется бетоном после монтажа. Ванты закрепляются в опорном контуре с помощью анкерных устройств, обеспечивающих возможность регулирования их длины во время монтажа и предварительного напряжения.

Покрытия висячих железобетонных оболочек выполняются из сборных железобетонных плит (обычно из легкого бетона), которые крепятся к вантам с помощью выпусков рабочей арматуры, специальных крюков или иных приспособлений (рис. 13.11, ж). В общем случае при возведении висячих оболочек рекомендуется укладывать бетон в швы, расположенные между опорным контуром и крайними плитами, в последнюю очередь с целью уменьшения краевых изгибающих моментов. В случае применения напрягающих цементов технология замоноличивания швов разрабатывается специально.

Расчет висячих железобетонных оболочек слагается из расчета несущих вант, опорных конструкций и покрытия по вантам и производится как для стадии монтажа, так и эксплуатации. Предполагается, что вертикальная нагрузка воспринимается одними вантами, работающими подобно нитям только на растяжение.

Расчет опорных конструкции выполняют на нагрузки от собственного веса и реакции наш и решением (кольцо, рама, балка и т. п.). Закрепление пат в опорном контуре и внутреннем кольце должно проектироваться так, чтобы линия действия усилий в ванте проходила через центр тяжести речного сечения кольца (рис. 13.11, з).

Сборные железобетонные плиты покрытия по вантам рассчитывают как самостоятельные элементы на усилия, возникающие в процессе изготовления и монтажа, а также на усилия, возникающие при натяжении вант и эксплуатационных нагрузках. Во многих случаях, когда стрела провеса нити f≥(1/20)l, ванты можно рассматривать как нерастяжимые абсолютно гибкие нити. При более пологих покрытиях необходимо учитывать дополнительное провисание вант вследствие их растяжимости.

Рис. 13.12. К расчету висячих покрытий

Рассмотрим усилия, возникающие под воздействием вертикальной равномерно распределенной нагрузки в отдельной гибкой нерастяжимой нити, закрепленной на опорах, расположенных на одном уровне (рис. 13.12, a). Горизонтальные (Н_А и Н_B) и вертикальные (V_A и V_B) составляющие реакций R_A и R_B определяют из условий равновесия:

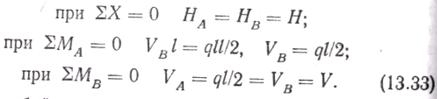
Для любой точки С нити справедливо условие

где М_с — балочный момент в рассматриваемой точке С; у_с — стрела провисания нити в той же точке, отсюда

и для х=l/2 получим

Продольное расчетное усилие в гибкой нити

Для системы с радиальным расположением вант в покрытии с круглым планом (рис. 13.12, б) аналогично предыдущему получим

где q₀ = qb.

От вант на опорное кольцо передаются радиальные усилия интенсивностью H₁ = H/b, направленные внутрь области покрытия. Сжимающие усилия в контурном кольце будут

 

 

 

ВОПРОС ДЛЯ САМОПРОВЕРКИ:

1. В чем заключается принципиальное отличие работы оболочек от плоских конструкций покрытий?

2. Достоинства и недостатки тонкостенных пространственных покрытий.

3. Классификация тонкостенных пространственных покрытий.

4. Сформулируйте предпосылки технической теории пологих оболочек, запишите разрешающую систему основных уравнений и объясните физический смысл входящих в нее величин.

5. Условия безмоментного напряженного состояния в оболочках. Система разрешающих уравнений. Возможные методы ее решения.

6. Конструкции и основные принципы расчета оболочек положительной гауссовой кривизны, куполов, гипаров, длинных и коротких цилиндрических оболочек, висячих покрытий.