Рассмотренные выше примеры представляют лишь малую часть из того множества ВР, которые имеют место в различных областях техники, социологии, экономики и пр. Основная цель этой книги состоит в том, чтобы обучиться методам формирования выводов и прогнозов из анализа наблюдаемых ВР. Для достижения этой главной цели следует получить подробные ответы на следующие вопросы, которые можно считать целями следующего уровня, в частности:
- как описать наблюдаемый временной ряд?
- каким образом подобрать модель ряда?
- что нужно сделать для формирования прогноза ряда?
- можно ли управлять наблюдаемым рядом?
Описание. Первым шагом при анализе ВР, как правило, является представление в виде графической зависимости наблюдаемого параметра от времени и рассмотрение суммарных статистик регистрируемых данных. В качестве примера в табл.1.1 приведены такие статистики, соответствующие ВР, график которого приведен на рис.1.1.
Графическое представление ВР позволяет визуально оценить наличие различных особенностей. Аналитик должен принимать во внимание поворотные точки тренда, ступенчатые изменения уровня, проявление «интервенций» ряда, разрывы, сезонные колебания.
Таблица 1.1 Статистики выборочных данных
| Показатели выборки | Значения показателей |
| Среднее | 78,91 |
| Стандартная ошибка | 0,27 |
| Медиана | 79,55 |
| Мода | 78 |
| Стандартное отклонение | 2,73 |
| Дисперсия выборки | 7,45 |
| Эксцесс | 0,65 |
| Асимметричность | -0,88 |
| Интервал | 14 |
| Минимум | 69,77 |
| Максимум | 83,77 |
| Сумма | 7970,31 |
Моделирование. При анализе ВР необходимо подобрать гипотетическую модель, с помощью которой можно описать наблюдаемые данные. После того, как подходящий класс моделей выбран, требуется оценить параметры модели, убедиться в пригодности этой модели для зарегистрированных наблюдений и применить подобранную модель для проверки механизма генерации наблюдаемого ряда. Такая модель может быть использована и для компактного описания анализируемого ВР. Любая модель основывается на прошлых значениях наблюдаемого параметра, и, по существу, все модели являются только аппроксимацией реальных данных. Вследствие этого некоторые исследователи считают подбор модели для описания ВР скорее искусством, чем наукой.
Прогнозирование. Имея наблюдаемый ВР и подобранную модель, можно перейти к задаче прогнозирования, т.е. определить по прошлым и настоящему значениям ВР величину прогнозной характеристики на определенном горизонте, под которым понимается временной промежуток, простирающийся за последним значением ВР. В англоязычной литературе для термина, определяющего «прогноз», используются два понятия: prediction и forecast. Многие зарубежные авторы не делают различия между ними, применяя их попеременно. Иногда разъясняется, что первый термин «prediction» относится скорее к субъективным методам прогноза (здесь уместны такие термины на русском языке как угадывание, предсказание), а второй «forecast» - к объективным (здесь речь идет о характеристике, полученной путем расчета, и сам термин предпочтительней называть прогноз).
Сделаем некоторые разъяснения, относящиеся к прогнозированию. Этот процесс, по существу, представляет собой форму экстраполяции, так как используется подобранная модель, по которой находятся значения ряда за диапазоном, где подбиралась модель. При проведении прогноза экстраполяция неизбежна, хотя среди статистиков эта операция не пользуется большой популярностью. Однако необходимо учитывать, что прогнозные оценки, которые определяют будущие значения процесса, должны быть похожи на прошлое временного ряда.
Управление. Иногда анализ ВР проводится с целью улучшения управляемости некоторой физической или экономической системы. Например, сгенерированный ряд, построенный по подобранной модели, может служить для оценки качества процесса производства конкретных изделий, где с помощью модели необходимо поддерживать высокий уровень качества. При выдаче кредита в банке можно оценивать величину кредитного риска, учитывая временные изменения характеристик заемщика.
Предположим, что имеется наблюдаемый ВР x 1, x 2,..., xN и необходимо спрогнозировать его будущее значение, например, xN + h. Величина h называется горизонтом прогноза, а значение прогноза xN + h, сделанное в момент времени N на h шагов вперед, обозначим как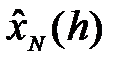 
. Отметим, что здесь важно указать как время, в которое делается прогноз, так и величину горизонта.
Метод прогнозирования представляет собой процедуру вычисления прогноза из настоящего и прошлых значений наблюдаемого ряда. По существу, этот метод может являться алгоритмическим правилом, не зависящим от лежащей в основе вероятностной модели. Альтернативно, метод прогнозирования может быть реализован из идентификации конкретной модели для выбранных данных. Таким образом, два термина «метод» и «модель» должны различаться. К сожалению, термин «модель прогнозирования» используется довольно широко в литературе и иногда ошибочно используется для описания метода прогнозирования.
Перед введением понятий стационарности и автокорреляции ВР кратко укажем основные шаги на пути формирования прогнозных характеристик ряда:
1. Построить график ВР и оценить его отличительные особенности, в частности, наличие тренда, сезонных составляющих, резких изменений в поведении.
2. Удалить тренд и сезонный компонент (если это возможно) для получения стационарных остатков. Для решения этой задачи иногда необходимо воспользоваться предварительным преобразованием данных или так называемым дифференцированием ряда (см.далее п.1.6). В любом случае вне зависимости от примененного метода нужно стремиться получить стационарный ряд, чьи значения рассматриваются как остатки.
3. Выбрать модель для подгонки этих остатков, используя различные статистики, например, выборочную автокорреляционную функцию.
4.Вычислить прогнозное значение для остатков и затем сделать обратное преобразование для получения прогноза исходного ряда.
