Задача на движение заряженной частицы по окружности в магнитном поле под действием силы Лоренца. Использовать термин: область локализации заряженной частицы. Найти период обращения частицы, радиус дуги окружности, скорость и импульс частицы, отношение заряда частицы к ее массе, величину вектора магнитной индукции.
Решение.
На движущуюся в магнитном поле заряженную частицу действует магнитная сила – сила Лоренца
где 
– угол между вектором 
и вектором магнитной индукции 
.
Если скорость заряженной частицы перпендикулярна вектору магнитной индукции, движение частицы происходит по окружности радиуса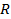 
. Область локализации частицы в этом случае равна 2 .
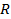Запишем уравнение второго закона Ньютона: произведение массы частицы на нормальное ускорение 
равно силе Лоренца:
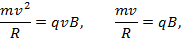
Откуда
Период обращения частицы по окружности равен
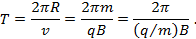
Импульс частицы равен
Задача на вычисление силы 
, действующей со стороны магнитного поля с магнитной индукцией 
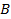на проводник длины 
с током 
.
Решение.
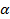
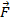
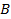Сила , действующая со стороны магнитного поля с магнитной индукцией на проводник длины с током , называется силой Ампера и равна векторному произведению векторов и .
Направление этой силы можно найти по правилу левой руки или по правилу буравчика (правого винта). А величину ее можно рассчитать по формуле
Задача. на закон Ома для замкнутой цепи. Найти напряжение на внешнем участке, напряжение на внутреннем участке и разность потенциалов на зажимах источника тока.
Решение.
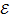
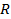
Закон Ома для замкнутой цепи:
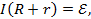
откуда
Напряжение на внутреннем участке цепи равно произведению силы тока на сопротивление внутреннего участкацепи:
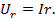
Напряжение на внешнем участке цепи равно произведению силы тока на сопротивление внешнего участкацепи:
Разность потенциалов на источнике тока по модулю равна напряжению на внешнем участке цепи:
Задача. Источник плоской бегущей волны колеблетсяпо закону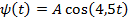 
. Скорость волны равна 1,5 м/с. Найдите длину волны.
Решение.
Из данного закона колебаний нам известны амплитуда колебаний 
и циклическая частота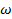 
, равная 4,5 1/с. Для вычисления длины волны используем формулы
Задача. Напишите уравнение плоской бегущей волны, распространяющейся со скоростью 
, если источник колебаний колеблется по закону 
.
Решение.
Из данного закона колебаний нам известны амплитуда колебаний и циклическая частота 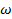. Для написания уравнения волны в канонической форме нам нужно только узнать величину волнового числа 
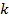, которую мы найдем по формуле
Получим
Задача. Дано уравнение плоской бегущей волны 
. Найдите скорость этой волны,длину волны, период колебаний и частоту волны в Гц.
Решение.
Если записано уравнение волны в канонической форме, то нам известна циклическая частота 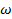и волновое число 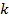по числам, которые стоят соответственно перед 
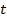и 
.
Скорость этой волны, длину волны, период колебаний и частоту волны в Гц найдем по формулам
Задача. Составить уравнение волны при любой заданной паре необходимых характеристик. Использовать все формулы связи между 
.
Решение.
Каноническое уравнение волны выглядит следующим образом:
Для его составления нужно вычислить циклическую частоту колебаний 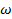по нужной формуле, исходя из заданных характеристик:
и вставить полученное число или выражение перед .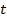
Затем нужно вычислить волновое число 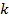по нужной формуле, исходя из заданных характеристик:
и вставить полученное число или выражение перед .
