Две несжимаемые взаимно нерастворимые жидкости

Рассмотрим совместное движение двух несжимаемых и взаимно нерастворимых жидкостей в трубе вдоль ее оси х (рис. 6). Будем считать, что движение происходит при постоянной температуре, т. е. процесс изотермический. Примером таких жидкостей могут быть нефть и вода. Выделим в трубе два сечения 1 — 1 и 2 — 2 соответственно ид расстоянии х и от начала оси х. Объем, заключенный между этими сечениями, обозначим через 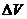. В этом объеме находятся жидкости 1 и 2. Процесс рассматриваем в единицу времени или за промежуток времени . Задаемся соотношением между объемами этих жидкостей. Отношение объема одной жидкости или другой к объему, занимаемому обеими жидкостями 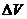, называется насыщенностью и обозначается соответственно через или S ₂ (в долях или процентах).

Обозначим плотность первой жидкости объем этой жидкости, проходящей через сечение 1 — 1 за единицу времени, , и проходящей через сечение 2 — 2, — Q ₁₂. Для второй жидкости введем соответтвенно обозначения . Тогда масса первой жидкости, прошедшей через сечение 1 — 1, будет а масса второй жидкости . В случае движения одной несжимаемой жидкости, т. е. когда S ₁ = 1 (или S ₂ = 0), Q ₁ = Q ₂₂ (или Q ₂ = Q ₂₂). Ввиду того, что в объеме 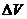содержится объем первой жидкости, объем

Рис. 6.

второй жидкости и соотношения их в объеме AV могут изменяться, то в общем случае

и . (1.36)

Поясним это на конкретном примере.

Пусть в объеме 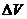= 10 м³ нефтенасыщенность составляет 50%, т. е. в нем содержится 5 м⁵ воды. Количество жидкости, протекающей через сечение 1 — 1 (см. рис. 6) и вытекающей из сечения 2 — 2, может отличаться друг от друга. Так, если через сечение 1 — 1 поступает 2 м⁵ нефти, то через сечение 2 — 2 может быть отобрано 2 м³ нефти, а может быть больше или меньше, но не больше 7 м³ (суммы объема нефти в общем объеме и объема нефти, поступившей через сечение 2 — 2, должны быть равны объему нефти, поступающей в сечение 1 — 1). S ₁ не изменяется во времени, т. е. процесс движения установившийся.

Если через сечение 2 — 2 отбирается нефти больше, чем втекает через сечение 1 — 1, то S ₁ уменьшается. Так, если из сечения 2—2 отбирается 3 м³ нефти, а через сечение 1 — 1 поступает 2 м³, то

т. е. нефтенасыщенность снизится на 11)%.

Если через сечение 1 — 1 поступает 1 м³ воды, то из сечения 2 — 2 может быть отобрана вода в количестве, равном, большем или меньшем чем 1 м^а, но в соответствии с поступившим в сечение 1 — 1 и отобранном из сечения 2 — 2 объемом нефти, т. е. должен быть соблюден следующий баланс:

Следовательно, для рассмотренного примера

= 2+ 1-3 = 0.

Таким образом, ввиду несжимаемости жидкостей сумма их объемов, поступивших в сечение 1 — 1, равна сумме объемов жидкостей, вытекающих из сечения 2—2,

(1-37)

Формула (1.37) отражает закон постоянства массы в конечной форме.

Масса каждой жидкости, а также сумма их масс в объеме 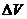во времени не постоянна. Так, в приведенном выше примере объем нефти в объеме 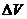станет равным 4м³,а объем воды — 6м³. При = 800 т/м³ и =1000 1 /м³ первоначальная масса жидкостей, находящихся в объеме 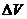, составляла G (t) = (0,8-5 -+- 1 -5) = 9 т.

После прохождения отмеченных объемов жидкостей через некоторое время масса их в том же объеме составит = 0,8*4+l*6 = 9,2 т. Следовательно, вес жидкости в объеме 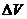увеличивается на 0,2 т. Разность между массой жидкости, втекающей через сечение 1—1 и вытекающей через сечение 2 — 2, идет на изменение насыщенности в объеме .

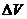, (I.38)

где Аа_г — изменение нефтенасыщенности (в приведенном выше примере = 10%).

Рассмотрим процесс совместного движения двух жидкостей,, характеризующийся величинами Q ₁ Q ₂, S ₁ и S ₂, которые меняются; как вдоль оси х, так и во времени.

Запишем уравнения (1.37) и (1.38) для любого сечения и в любой момент времени. Процесс исследуется в интервале х за промежуток времени . Чтобы получить выражения (1.37) и (1.38) для любого сечения и в любой момент времени, необходимо, чтобы .

В приведенном примере Q ₁ и Q ₁₂ принимались (и в дальнейшем принимаются) постоянными во времени, но они могут быть и переменными.

Таким образом, для первой жидкости в сечении 1—1 имеем (, а в сечении 2 — 2 , соответственно для второй жидкости имеем ( ₂ (х, t) и . Следовательно,

В момент времени t в сечении 1—1 насыщенность будет S ₁ (х, t), через промежуток времени насыщенность станет , а в сечении 2 — 2 соответственно и . Запишем закон постоянства массы (1.37) для данного элементарного объема

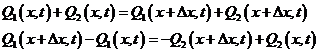Разделим на и перейдем к пределу при

Выражение (1.40) представляет собой закон постоянства массы в дифференциальной форме.

Запишем выражение (1.38) для элемента объема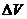

Здесь — изменение насыщенности во времени из-за накопления первой жидкости.

Отметим, что будут иметь одинаковые значения при . Следовательно, изменение насыщенности в объеме 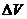(при можно выразить как , так и .

В выражении (1.41) левая часть умножена на , так как масса жидкости G отнесена к единице времени, а процесс рассматривается в течение времени .

Если масса первой жидкости в объеме 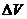увеличивается, то накопление имеет положительный знак

Это может быть в случае, если , т. е. масса первой жидкости, поступающей через сечение 1 — 1, больше отбора ее через сечение 2 — 2. Поэтому в (1.41) знак в правой части должен быть противоположным знаку в левой части, т. е.

(1.42)

или, зная, что ,

(1.43)

Разделив обе части (1.43) на и перейдя к пределу при

откуда для первой жидкости, получим

Заметим, что (1.44), (1.45) и (1.40) являются независимыми уравнениями, а (1.46) и (1.47) могут быть получены из них. Или формула (1.40) может быть получена из уравнений (1.44), (1.45), (1.46), (1.47). Покажем это на примере.

Сложив (1.45) и (1.47), получим

Так как , то

Как было отмечено выше, в рассматриваемом примере необходимо определить Q ₁ Q ₂ и S₁ Зная же S ₁, можно определить S ₂ = 1— S ₁, т. е. для трех величин имеется два уравнения (1.45) и (1.47).

Рассмотрим движение смеси жидкости и растворенного в ней газа и выделенном объеме трубы (см. рис. 6). Будем считать, что движение происходит при постоянной температуре, т. е. процесс изотермический. Принимается, что жидкость несжимаема, а газ, как обычно, сжимаем.

В данном случае через сечение 1—1 поступают жидкость с растворенным в ней газом и газ в свободном состоянии. В объеме 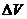имеется насыщенность газом и жидкостью. Причем насыщенность газом в отличие от предыдущего случая может изменяться как в результате изменения количества газа в этом объеме, так и вследствие его сжимаемости.

Обозначения приняты те же, что и в предыдущем случае, но вместо первой жидкости взят свободный газ, а вместо второй — насыщенная газом жидкость.

Введем следующие дополнительные обозначения для масс газа и жидкости: G ₃ — масса газа в растворенном состоянии, поступающего через сечение 1 — 1 за единицу времени; G ₃₂ — масса газа в растворенном состоянии, выходящего через сечение 2 — 2 за единицу времени; G₄ — масса растворенного газа в единице объема жидкости за единицу времени.

Принимаем, что масса растворенного в жидкости газа, по сравнению с массой самой жидкости очень мала. Поэтому ею можно пренебречь, т. е. G₂ и G₂₂ рассмотрим как массу жидкости. Но это предположение не всегда справедливо. Для иллюстрации этого приведем следующий пример. Пусть имеется нефть, плотность которой (при 20° С) = 780 кг/м³, и газ, относительная плотность которого (по воздуху) А = 0,7; газовый фактор Г = 100 м³/м³.

Относительная молекулярная масса газа будет

М₁ = М₃ = 29-0,7 = 20,3,

где М₃ — молекулярный вес воздуха.

Число киломолей газа, растворенных в 1 м³ нефти,

где 22,4 м³ — объем 1 кмоль газа при нормальных условиях.

Кажущаяся плотность газа (при относительной плотности 0,7) в нефти (плотность 780 кг/м³) = 320 кг/м³. Следовательно, увеличение объема 1 м³ нефти, вызванное растворением газа, составит

м³.

Общий объем насыщенной газом нефти, отнесенной к атмосферным условиям, будет

м³

а, масса нефти с растворенным в пей газом

кг,

где G_o — вес ненасыщенной нефти; V — объем ненасыщенной нефти. Плотность нефти с растворенным в ней газом рассчитывается по формуле

кг/м ³.

Следовательно, при растворении газа в жидкости масса ее увели чивается.

Рассмотрим изменение массы жидкости в элементарном объеме, т. е. запишем закон постоянства масс жидкости (по аналогии с предыдущим случаем)

. (I.49)

Запишем закон постоянства массы для газовой фазы. Изменение массы газа за время — разность массы газа, поступающего через сечение 1 — 1 (см. рис. 6), и массы газа, выходящего из сечения 2 — 2, т. е. , соответствует изменению массы газа в рассматриваемом объеме и равно сумме изменения масс растворенного и свободного газа в объеме 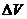, т. е. равно .

Таким образом, можно записать

l. (I.49)

В соответствии с ранее принятым (в предыдущем случае) .

Изменение G ₁ происходит в результате изменения . Следовательно, .

Для того чтобы уравнения (1.49) и (1.49') записать для любого момента времени и для любого сечения, проделаем следующее.

Запишем уравнение (1.49), согласно принятым обозначениям, в виде

. (1.50)

Если масса жидкости в объеме 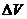увеличивается, то накопление имеет положительный знак, т. е. . Это может быть при , т. е. когда масса жидкости, поступающей в сечение

1 — 1, больше массы жидкости, отбираемой из сечения 2 — 2. Поэтому в (1.50) знак в правой части должен быть противоположным знаку в левой части

Разделив обе части (1.51) на и и перейдя к пределу при , получим

Из уравнения (1.49') имеем

Разделив обе части уравнения (1.54) на и перейдя к пределу при

Объем жидкости, поступающей в сечение 1 — 1, будет —. .Следовательно, в объеме — содержится масса растворенного газа —-, т. е.

. (I.56)

Таким образом, в трех уравнениях (1.52), (1.55) и (1.56) имеются неизвестные: G_x, G ₂, G ₃, G₄, S ₂ и .

Приведенному выше примеру аналогичен случай движения газо-конденсатной смесив трубах или в пористой среде. В газоконденсатной системе в отличие от газонефтяной при снижении давления выпадает жидкость-конденсат. Следовательно, в выделенный объем поступает газ с конденсатом. Принимая, что выпавший конденсат неподвижен, и пренебрегая изменением массы газа от выпадения конденсата, можно применить закон постоянства массы для определения измене-ния насыщенности конденсатом рассматриваемого объема.

Через сечение 1 — 1 в единицу времени прошли масса газа G ₁ и масса конденсата G₂. Через сечение 2 — 2 отобраны масса газа и масса конденсата G₂₂. Тогда масса конденсата, накопившегося в объеме в единицу времени,

Это приращение массы конденсата приведет при условии несжимаемости конденсата ( = const) к изменению объема в единицу вре мени на величину .

За отрезок времени изменение объема будет . Это изменение объема приведет к изменению насыщенности конденсатом на величину .

Аналогично предыдущему случаю запишем

Знак минус перед правой частью поставлен, исходя из следующих соображений: если , то насыщенность конденсата в объеме 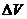уменьшается, т. е. , и наоборот.

Разделив обе части уравнения (1.57) на и и перейдя к пределу при , получим

Так как было принято, что масса газа не изменяется при выпадении конденсата, то для газовой фазы можно написать закон постоянства массы в форме, записанной выше,

В уравнениях (1.58) и (1.59), описывающих процесс движения газо-конденсатной системы, имеются четыре неизвестных.

Закон сохранения энергии

Покажем на примерах, как можно применять закон сохранения энергии для описания некоторых физических процессов.

В основном будут рассматриваться механический и тепловой процессы, поэтому сформулируем для них закон сохранения энергии. Для механических процессов сумма кинетической и потенциальной энергии постоянна.

При тепловых процессах закон сохранения энергии, или первый закон термодинамики, записывается так: бесконечно малое изменение внутренней энергии состоит из двух частей — из количества тепла, полученного телом, и произведенной телом работы.

Работа при поступлении тепла зависит от начального и конечного состояния тела и от пути, по которому изменяется состояние тела. Поэтому нельзя рассматривать тепловой эффект процесса как разность этих количеств в конечном и начальном состояниях.

С поглощением тепла в количестве dQ температура повышается на величину dT.

Отношение (где т — масса тела) называется теплоемкостью тела. В физике пользуются теплоемкостью при постоянном давлении с_р и теплоемкостью при постоянном объеме .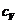

Применим первый закон термодинамики для исследования процесса распространения тепла в теле.

Рассматриваются два сечения 1 — 1 и 2—2 (рис. 7). Тело имеет какую-то определенную начальную температуру. К одному концу тела подводится источник тепла или холода. Соответственно этому в теле происходит нагревание или охлаждение.

Температура в какой-либо точке тела будет зависеть от расстояния точки до места подвода тепла и времени

Т = Т(х, t).

На текущее распределение температуры в теле оказывает влияние начальное распределение температуры, а также условия в концевых сечениях тел, в частности от температуры на обоих концах тела.

В приведенном примере через сечение 1—1 в единицу времени подводится количество тепла, равное Q (х, t). Через сечение 2 — 2 в единицу времени отводится количество тепла, равное . Разность между этими количествами тепла

в соответствии с первым законом термодинамики затрачивается на изменение температуры в отсеке между сечениями 1 — 1 и 2 — 2.

Если , то тело нагревается, в противном случае — охлаждается, т. е. в первом случае

,(1.61)

а во втором — .

При изменении количества подводимого и отводимого тепла па величину температура тела (в соответствии с законом сохранения энергии и определением теплоемкости) должна изменяться на величину

где — элементарная масса тела; S — площадь поперечного сечения тела; — плотность тела.

Так как при и при , то в правой части (1.62) поставлен знак минус.

Подставив в (1.62) значения и соответственно из (1.60), (1.61) н разделив его на на и перейдя к пределу при ,

получим

Таким образом, в одном уравнении получаем два неизвестных Q и Т. Покажем применение закона сохранения механической энергии. Обозначим через — касательное напряжение. Выведем дифференциальное уравнение движения в круглой цилиндрической трубе вдоль кольца. Для этого выделим в зоне на расстоянии 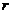от оси трубы элементарный кольцевой слой толщиной dr и длиной и составим уравнение равновесия сил, действующих на выделенный элемент. Этими силами будут: тормозящая сила , ускоряющая сила , сила давления и сила инерции .

По принципу Д'Аламбера, сумма этих сил должна равняться нулю. Если при этом учесть, что первая и последняя из этих сил действуют в направлении, обратном действию остальных двух сил, то

Пренебрегая величиной drdx по сравнению с другими членами, получаем

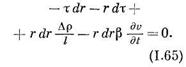
Рис.8.

Рассмотрим колебание натянутой упругой струны. Колебания принимаются малыми. Это позволяет пренебречь увеличением длины

струны, что приводит к постоянству натяжения в любом сечении и в любой момент времени. Пренебрегаем трением, т. е. диссипация (рассеяние) энергии принимается равной нулю (так как приток энергии извне принимается равным нулю). Предполагаем, что начальный момент времени соответствует состоянию равновесия. Например, в начальный момент времени струна натянута, находится в горизонтальном положении и концы ее закреплены. Для того чтобы начался процесс колебания струны, необходимо ее вывести из положения иавновесия, положим, начальным импульсом. Обозначим отклонение струны от ее положения равновесия через .

На рис. 8 цифрами 1—1 и 2—2 обозначены сечения, в которых закреплены концы струны. Выделим на расстоянии х от начала оси х элементарный отрезок струны между сечениями, обозначенными цифрами 3 — 4.

Для определения кинетиче ской энергии необходимо найти скорость точек этого отрезка струны. Смещение (отклонение от положения равновесия) точки 3 будет а через интервал времени оно составит .

Средняя скорость этой точки соответствует

Ввиду того, что подынтегральное выражение ни в одной из точек не может быть меньше нуля, то интеграл равен нулю лишь тогда, когда подынтегральное выражение равно нулю,

Перенесем второе слагаемое в правую часть равенства и разделим последнее на -— (зная, что -— =£= 0). При этом получим

Равенство (1.77) представляет собой дифференциальное уравнение колебания струны. В этом случае имеем одно уравнение и одно неизвестное. Другое неизвестное — натяжение струны — было принято постоянным и тем самым исключено как неизвестное.

Продольное колебание стержня происходит в процессе спуска-подъема бурильных труб или же в процессе непосредственного бурения. Так, например, если имеется шарошечное долото, которое в процессе бурения производит колебательное движение, то в упругих бурильных трубах возникает продольное колебание.

Способ бурения принимается турбинным, так как при роторном в бурильных трубах возникают крутильные колебания, вызванные вращением инструмента. Чтобы не усложнять вывода, трением пренебрегаем. Дифференциальное уравнение в этом случае имеет такой же вид, как и для колебания струны. Но в отличие от колебания струны при продольном колебании упругие напряжения, возникающие в каждом сечении, уже не могут быть приняты постоянными как в сечениях, так и во времени.

Дифференциальное уравнение для этого случая можно получить из уравнения движения.

В данном продольном стержне смещение происходит вдоль оси.

Обозначим через смещение вдоль оси ох (см. рис. 9).

Скорость вдоль оси Ox

Ускорение вдоль оси Ox

Рис.10

Упругое напряжение в сечении 1 — 1 в момент времени t будет F (x, t), а в сечении 2 — 2 — будет .

Согласно второму закону Ньютона можно записать

где — плотность; F — площадь поперечного сечения стержня. Разделив уравнение (1.78) на Ах и перейдя к пределу при , получим

Таким образом, имеем одно уравнение и два неизвестных и F.

Данные уравнения можно получить также, исходя из закона сохранения энергии. Покажем на одном примере, что дифференциальные уравнения, полученные из закона Ньютона и на основе закона сохранения энергии, одни и те же.

Рассмотрим колебание груза, подвешенного к упругой нити. Примем, что сила упругости пропорциональна удлинению х (рис. 10).

На рис. 10 показаны: 1 — положение равновесия, 2 — отклонение от положения равновесия, которое изменяется в зависимости от нремени. Если в начальный момент времени груз находится в пололожении равновесия, то х = 0.

Кинетическая энергия в положепии 2 равна , где т —масса; - скорость груза.

Потенциальная энергия — это энергия упругости нити. Силы упругости приняты пропорциональными х, т. е. кх совершает элементарную работу kxdx, соответствующую элементарной потенциальной энергии. В положении 2 потенциальная энергия определяется как

где Ф — полная энергия в положепии 2. Дифференцируя (1.81) по t, получаем

тх"х' -\- кхх' = 0.

При

тх" + кх = 0. (1.82)

Уравнение (1.82) и есть выражение второго закона Ньютона. Во всех приведенных случаях, как правило, число неизвестных было больше числа уравнений, за исключением одного случая — поперечного колебания струны. Однако и в последнем, как было отмечено, одно неизвестное — натяжение струны — исключили, приняв его постоянным. Рассмотрим, каким образом можно получить недостающие уравнения. Например, для движения смеси двух несжимаемых жидкостей необходимо составить еще одно уравнение. Но в этом случае процесс определяется и давлением. Поэтому необходимо иметь два уравнения для нахождения Q ₁ и Q ₂.

При изотермическом совместном движении газа и жидкости в трубопроводе неизвестными были и V, а уравнение — одно. Но, как известно, связано с давлением при помощи уравнения состояния Клайперона — Менделеева

где р — давление.

Однако при этом появляется новое неизвестное р, т. е. опять не хватает одного уравнения. Приведенное выше уравнение соответствовало закону постоянства массы. Для исследуемого явления необходимо применить еще закон сохранения энергии, например в виде уравнения Бернулли. Но в этом случае появится новое неизвестное — работа сил трения, т. е. требуется опять одно уравнение для определения силы трения. Это уравнение устанавливается экспериментально.

Для совместного движения несжимаемых жидкостей закон сохранения энергии приводит также к необходимости определения силы трения. Указанный процесс характеризуется и давлением. Поэтому и в этом случае необходимо экспериментально составить одно уравнение для сил трения. Если движение неизотермическое, то следует применить и первый закон термодинамики. Тогда появятся два неизвестных Qи Т, связанных одним уравнением типа

т. е. и в этом случае необходимо определить одну экспериментальную зависимость для Q.

При изотермическом движении газированной жидкости в трубопроводе или при фильтрации газированной жидкости в пористой среде плотность газа р связана с давлением р. Появляется еще одно неизвестное р. Вводя понятие массовой скорости для жидкости w ₁ и газа w ₂, можно через них вычислить соответственно G ₁ и G ₂. Неизвестными в этом случае являются . Таким образом, необходимо экспериментально определить зависимости для w ₁, w ₂ и G ₃.

При использовании закона сохранения энергии в этом случае необходимо знать работу силы трения, т. е. силу трения (новое неизвестное), причем применение закона сохранения энергии не уменьшает числа недостающих уравнений. Наоборот, количество уравнений увеличивается, соответственно этому увеличивается и количество неизвестных. При движении газоконденсатной смеси в трубах или в пористой среде имеем два уравнения и четыре неизвестных . Плотность р₁ связана с давлением при помощи уравнения состояния.

Таким образом, необходимо экспериментально определить две зависимости — для G ₁ и G ₂.

При исследовании процесса распространения тепла в теле имеем два неизвестных Q и Т и одно уравнение. Закон постоянства массы выполняется тождественно и недостающее уравнение для Q определяется экспериментально.

Для продольного колебания стержня закон постоянства массы также выполняется тождественно и не дает нового уравнения. В этом случае недостает одного уравнения для вычисления упругих напряжений, которое находят экспериментально.

Для механических процессов необходимы данпые о характерных снойствах рассматриваемой сплошной среды. Эти свойства описываются так называемым определяющим уравнением, которое представляет собой уравнение, описывающее механическую модель.

Ниже будут рассмотрены различные механические модели.

В связи с тем, что тепловые и диффузионные процессы приобретают все большее значение в нефтяной промышленности, будут рассмотрены недостающие уравнения при описании этих процессов. Метод моделирования широко применяется в различных отраслях промышленности, в частности в нефтяной. Учитывая это, а также необходимость расчета электрических и магнитных цепей для различных задач нефтедобычи и бурения, в специальнем параграфе рассматриваем основные законы электричества и магнетизма. В заключение этой главы приведем еще одно необходимое уравнение состояния — скалярное соотношение между плотностью, давлением и температурой.

Для некоторых механических задач часто берут такое уравнение состояния, которое не содержит температуры. Процессы, подчиняющиеся таким уравнениям состояния, называются баротропными.

Однородная несжимаемая жидкость представляет частный случая баротропной жидкости.

Важным частным случаем являются изотермические процессы, при которых температура сохраняетря постоянной, и адиабатические процессы, при которых отсутствует теплообмен.

3. МЕХАНИЧЕСКИЕ МОДЕЛИ

Механические свойства различных материалов могут быть описаны разными теоретическими схемами. Такие схемы позволяют давать качественные описания процесса деформации. Для построения замкнутой теории движения среды должна быть известна связь между кинематическим и динамическим состояниями частицы, в частности между напряжениями и деформациями, выражаемая при помощи механического уравнения состояния тела.

К простым средам относятся следующие тела: упругое, вязкое, жестко-пластическое. Механическое уравнение состояния упругого тела выражается при помощи закона Гука, который для одноосного напряженного состояния имеет вид:

, (I.83)

где — напряжение; Е — модуль Юнга; — относительная деформация.

Механическое уравнение состояния упругого тела изображается в виде механической модели, представляющей собой пружину (рис. 11).

Механическое уравнение состояния вязкого тела для одноосного напряженного состояния выражается при помощи закона Ньютона

. (1-84)

где — вязкость; - — скорость деформации.

Вязкое тело изображается моделью, состоящей из поршня, двигающегося в цилиндре с вязкой жидкостью (рис. 12).

Жестко-пластическое тело при напряжениях ниже предела текучести а_т не деформируется. В таком теле течение развивается лишь при напряжениях, удовлетворяющих условию текучести . Модель такой среды может быть изображена в виде площадки с кулоновым трением (рис. 13).

Выше были приведены три простейшие механические модели, иллюстрирующие механические уравнения состояния вязкого, упругого и жестко-пластического тела. Комбинируя эти простые модели,

Рис. 11. . Рпс. 12. Рис. 13.

можно рассматривать различные сложные среды. Так, упруго-пластическую среду можно характеризовать моделью, в которой

последовательно соединены упругий и пластический элементы (рис. 14).

Упруго-вязкая среда Фойхта характеризуется моделью, в которой параллельно соединены упругий и вязкий элементы (рис. 15).

Рис. 14. Рис. 15. Рис. 16.

Для такой среды полное напряжение будет складываться из напряжения, соответствующего упругой деформации, и напряжения, вызываемого вязким сопротивлением,

. (1.85)

В состоянии покоя, т. е. при , такая среда ведет себя как упругая. При в среде возникает постоянное напряжение . Если при t = 0, , то из (1.85) получим

Рассмотрим теперь среду, которой соответствует модель, состоящая из последовательно соединенных упругого и вязкого элементов (рис. 16). Для такой среды Максвеллом, получен следующий закон деформации:

где — - — скорость деформации; - скорость упругой деформации;

-скорость вязкой деформации.

Из закона Гука дифференцированием определим

Определив - из закона Ньютона (1.84) и подставив полученные значения из (1.88) и (1.87), получим

Если , то тело, описываемое уравнением (1.89), будет деформироваться с постоянной скоростью, т. е. течь подобно вязкой жидкости.

Теперь рассмотрим другой случай. Пусть в момент времени t = О на тело действует напряжение и соответствующее начальное

относительное удлинение, равное -—. Положим , что достигается, в частности, закреплением концов стержня. В этом случае и из уравнения (1.89)

Из (1.90) видно, что напряжение со временем изменяется и no-закону экспоненты при стремится к нулю (рис. 17). Уравнение Максвелла с качественной стороны описывает так называемую релаксацию напряжения, т. е. ослабление со временем напряженного состояния при неизменной деформации. В дальнейшем уравнение Максвелла будет нами использовано для конкретного объяснения явления вытекания глин в скважину в процессе проводки скважины и дальнейшей ее эксплуатации. Находясь под нагрузкой, твердые тела (в частности, цементный камень) медленно деформируются. С повышением температуры это явление текучести тел резко возрастает.

Текучесть твердых тел при высоких температурах обладает рядом характерных свойств и называется ползучестью, или крипом. Изучение ползучести твердых тел проводится опытным путем — растяжением стержней при постоянной температуре и фиксированных нагрузках.

Отложим на оси ординат относительное удлинение, а на оси абсцисс — общее время испытания t, тогда кривая длительных испытаний будет иметь вид, показанный на рис. 48. Отрезок ОА соответствует начальной деформации , полученной стержнем при его

Рис. 17. Рис.18.

нагружении. Отрезок АВ характеризует убывание скорости ползучести. С приближением к точке В уменьшение скорости деформации замедляется, и на участке ВС, называемом вторым периодом ползучести, скорость деформации практически становится постоянной. Указанный период, характеризуемый минимальной скоростью ползучести, бывает обычно наиболее длительным и заканчивается разрушением тела.

Вязко-пластическое тело изображается моделью, которая состоит из вязкого элемента и площадки с кулоновым трением, соединенных параллельно (рис. 19). Уравнение деформации вязко-пластического тела Шведова — Бингама имеет следующий вид:

где — предельное напряжение сдвига.

При то тело не деформируется. Из рис. 20 видно, что для ряда тел течение наступает только после определенной нагрузки, при этом скорость течения зависит от вязкости среды.

Для выражения механических свойств высокополимеров необходимо привлекать модели, состоящие из многих элементов. Обычно для таких моделей характерно большое число параметров. Авторы рассматривали двухпараметрические модели .

Рассмотрим модель (рис. 21), содержащую три параметра Е₁, Е₂, . Для такой среды закон деформации можно получить следующим образом.

Рис.19. Рис.20.

Напишем закон деформации для простых элементов I, II, III:

Рис. 21. Рис. 22.

а также для условий равновесия и неразрывности

Аналогично можно привести модель с четырьмя параметрами (Рис. 22).

4. ОБ УРАВНЕНИЯХ СОСТОЯНИЯ И ЗАКОНАХ ПЕРЕНОСА

Для описания состояний макрофизических свойств тел и переноса процесса взаимодействия применяется понятие обобщенного заряда — объем, масса и т. д. Величина заряда в теле определяет его состояние, а перенос его количественно характеризует процесс взаимодействия.

Величина заряда относится к экстенсивным величинам, т. е. к величинам, распределенным по объему. Заряд может переноситься под действием обобщенного потенциала — интенсивной величины, т. е. величины, распределенной по поверхности. К обобщенным потенциалам относятся температура, давление, электрический потенциал, напряжение и т. д.

Законы переноса определяют зависимость между потоками заряда и разностью потенциалов. Закон же состояния определяет зависимость между потенциалом и зарядом. Так, например, для жидких, газообразных и твердых однородных тел заряд — это объем, обобщенные потенциалы — давление и температура, уравнение состояния — зависимость, выражающая связь между объемом, давлением и температурой. Зависимость между напряжениями и деформациями — это механическое уравнение состояния.

Если поток заряда переносится в пространстве в одном направлении, то такой перенос называется одномерным, в случае же переноса в двух направлениях — плоским, а в трех направлениях — пространственным.

Наибольшее распространение получило уравнение Менделеева — Клайперона (pV = zRT, где р — давление, V — объем, R — газовая постоянная, Т — температура, °К, z — коэффициент сжимаемости).

Безразмерный коэффициент сжимаемости зависит от безразмерного давления и безразмерной температуры (р_кр и Т _кр — соответственно критическое давление и температура).

Для нефтепромысловой практики, учитывая точность расчетов, определяемую допусками, точностью исходной информации, а также точностью контрольно-измерительных приборов, коэффициент z можно принять равным единице, т. е. газ принимается идеальным. Так, например, для контроля давления наиболее совершенное средство — образцовые манометры, погрешность которых для некоторых манометров и интервалов давлений составляет +0,35% максимального давления. Если при трубопроводном транспорте газа давление в начале трубопровода близко 100 кГ/см², то применяется манометр со шкалой 100 кГ/см², причем погрешность будет 0,35 кГ/см². Учет коэффициента z при сравнительно небольшой протяженности газопровода внесет уточнение не более указанной погрешности.

Приведем пример, не имеющий прямого отношения к излагаемому, по хорошо иллюстрирующий отмеченное положение. При трубопроводном транспорте воды, учитывая допуски, точность расходомеров, погрешность в определении гидравлических сопротивлений также может достигнуть нескольких процентов. Часто в инженерных исследованиях это не учитывается. Например, точность рассчитанных величин не адекватна точности контрольно-измерительных приборов. Иногда составляют эмпирические уравнения, в которых влияние отдельных факторов меньше, чем точность, с которой может быть определена функция. Придавая большое значение этому вопросу, авторы посвятили специальный параграф краткому изложению теории ошибок, в основном имея в виду их прикладное значение для нефтепромысловой механики.

Приведем уравнение состояния жидкости, которое часто применяется в нефтегазопромысловой механике для баротропной жидкости,

где — плотность при давлении р₀; — коэффициент объемного упругого расширения жидкости.

Данное уравнение может быть аппроксимировано линейной зависимостью

Отмеченное справедливо для так называемых малосжимаемых жидкостей. Очень часто, идеализируя уравнение, не указывают условия, при которых эта идеализация практически приемлема.

Так, в рассматриваемом случае только по коэффициенту упругого расширения жидкости не могут быть отнесены к малосжимаемым. Это зависит и от интервала изменения давления, т. е. если имеются две жидкости и у одной коэффициент меньше, чем у другой, это не свидетельствует о возможности применения линейной аппроксимации. Необходимо обратить внимание на интервал изменения давления.

Рассмотрим критерии, которые позволяют выяснить условия, при которых следует учитывать упругость и сжимаемость жидкости. Так, например, при нестационарном движении вязкой жидкости в длинном трубопроводе, а также в пористой среде целесообразно применить понятие времени релаксации (ослабление состояния тела после прекращения воздействия, вызвавшего это состояние). Оценим порядок времени релаксации для движения в трубопроводе. Под порядком понимается порядок величины: секунды, десятки секунд, сотни секунд и т. д. Время релаксации будет зависеть от силы инерции, определяемой массой (плотностью) и вязкостью. Так как развитие профиля скоростей зависит в основном от радиуса, следовательно,

Нетрудно видеть, что из этих четырех величин может быть составлен один безразмерный параметр.

Приведенная зависимость представляется в виде степенной комбинации, что возможно при одном безразмерном параметре

Пользуясь размерностью величин, входящих в последнее уравнение, получаем

где Т, Р и L — соответственно размерности времени, силы и длины. В левой и правой части уравнения размерности должны быть одинаковые (однородность размерности). В левой части не имеется Р и L, точнее, они входят в нулевой степени. Следовательно, и в правой части Р и L должны быть в нулевой степени, Т — в первой, т. е.

Отсюда т₁ = 1; m ₃ = —1; m₂ = 2. Таким образом,

Время релаксации имеет порядок

Приведем численный пример. Через 4" трубопровод прокачивается вязкая нефть плотностью 0,8 и вязкостью 5 спз. Тогда

Таким образом, время релаксации порядка нескольких минут.

Если рабочий период трубопровода больше времени релаксации, то можно пренебречь упругостью жидкости и рассматривать движение как стационарное. При исследовании пускового периода трубопровода, время которого соизмеримо со временем релаксации, необходимо рассматривать нестационарное движение.

Для твердого скелета упругой пористой среды принимается следующее уравнение состояния:

где — объем норового пространства; — объем жидкости; V — начальный объем; — коэффициент сжимаемости.

Строго говоря,