1. Линейность преобразования Лапласа. Если f (t), g (t) - функции-оригиналы, имеющие изображения F (p), G (p), то их линейная комбинация α f (t) + β g (t) (α = cost, β = const)- тоже функция-оригинал, и α f (t) + β g (t)  α F (p) + β G (p).
α F (p) + β G (p).
Это свойство непосредственно следует из свойства линейности несобственного определённого интеграла. С его помощью можно более просто вывести изображения функций sin t, cos t, исходя из изображения  :
: 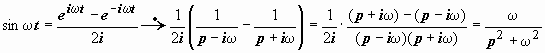 ;
;  . Далее,
. Далее,  ;
;  .
.
2. Теорема подобия. Если f (t) - функция-оригинал и f (t)  F (p), то для любого λ > 0
F (p), то для любого λ > 0  .
.
Док-во. 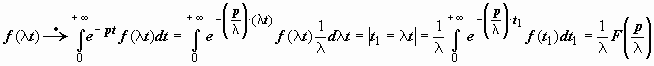 .
.
Иллюстрации применения этого свойства: если  , то
, то  ; если
; если  , то
, то  и т.д.
и т.д.
3. Теорема смещения. Если f (t)  F (p), то e α t f (t)
F (p), то e α t f (t)  F (p − α),. Здесь α - произвольное комплексное число.
F (p − α),. Здесь α - произвольное комплексное число.
Док-во. 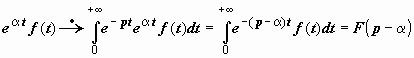 .
.
Иллюстрации применения этого свойства: если  , то
, то 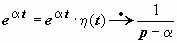 ; если
; если 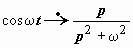 , то
, то  и т.д.
и т.д.
4. Теорема запаздывания. Если f (t)  F (p) (т.е. f (t) · η (t)
F (p) (т.е. f (t) · η (t)  F (p)), то f (t − t 0) · η (t − t 0)
F (p)), то f (t − t 0) · η (t − t 0)  e − t 0 · p · F (p) для любого числа t 0 ≥ 0.
e − t 0 · p · F (p) для любого числа t 0 ≥ 0.
Док-во. 


 .
.
Теорема запаздывания применяется для изображения функций импульсных, составных, периодических. Рассмотрим этот вопрос подробнее.
Импульсные функции.
а) Единичный импульс:  С помощью функции Хевисайда эта функция записывается так:
С помощью функции Хевисайда эта функция записывается так:  . Мы знаем, что
. Мы знаем, что  ; по теореме запаздывания (t 0 = 1)
; по теореме запаздывания (t 0 = 1)  , поэтому
, поэтому  .
.
б) Запаздывающий прямоугольный импульс: 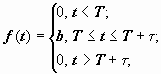 Здесь
Здесь 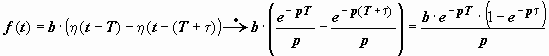 .
.
в) Треугольный импульс. Аналитически эта функция записывается так:  Изменение функции на переходе от участка T ≤ t ≤ T + τ к участку T + τ ≤ t ≤ T + 2τ равно
Изменение функции на переходе от участка T ≤ t ≤ T + τ к участку T + τ ≤ t ≤ T + 2τ равно  ; при переходе к участку t > 2τ изменение функции равно
; при переходе к участку t > 2τ изменение функции равно  , поэтому можно переписать
, поэтому можно переписать  , и, так как
, и, так как  ,
,  , то
, то 
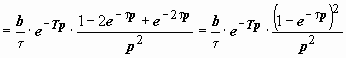 .
.
г) Синусоидальный импульс. 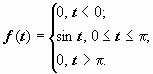 Здесь
Здесь  , поэтому
, поэтому  .
.
Составные функции. Пусть f (t) задаётся разными выражениями на различных участках области определения:
 . С помощью функции Хевисайда f (t) записывается так:
. С помощью функции Хевисайда f (t) записывается так: 
 , и теорема запаздывания позволяет получить изображение этой функции.
, и теорема запаздывания позволяет получить изображение этой функции.
Периодические функции. Пусть f (t)- периодическая при t > 0 функция с основным периодом, равным T. Обозначим f 1(t) функцию, описывающую первый период функции f (t):
 . Теперь
. Теперь 
 (каждое слагаемое описывает соответствующий период). Пусть
(каждое слагаемое описывает соответствующий период). Пусть  - изображение функции f 1(t). Тогда
- изображение функции f 1(t). Тогда 
 .
.
Найдём в качестве примера изображение функции { t } - дробной части числа t. Эта функция определяется так: { t } = t – n при n ≤ t < n + 1, n - целое число. Для неё  , или f 1(t) = t · [ η (t) − η (t − 1)] = t · η (t) − (t − 1) η (t − 1) − 1 · η (t − 1), поэтому
, или f 1(t) = t · [ η (t) − η (t − 1)] = t · η (t) − (t − 1) η (t − 1) − 1 · η (t − 1), поэтому  , и
, и  .
.
5. Интегрирование оригинала. Если f (t) - функция-оригинал, и f (t)  F (p), то
F (p), то  - тоже функция-оригинал, и
- тоже функция-оригинал, и  .
.
Док-во. 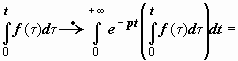 (это повторный интеграл, вычисляемый по области {0 ≤ t < +∞, 0 ≤ τ ≤ t }; меняем порядок интегрирования, это можно сделать, так как несобственный двойной интеграл сходится абсолютно)
(это повторный интеграл, вычисляемый по области {0 ≤ t < +∞, 0 ≤ τ ≤ t }; меняем порядок интегрирования, это можно сделать, так как несобственный двойной интеграл сходится абсолютно) 
 .
.
6. Дифференцирование оригинала. Если функция-оригинал f (t) имеет производную f ′(t), тоже являющуюся оригиналом, и f (t)  F (p), то f ′(t)
F (p), то f ′(t)  p F (p) − f (+0).
p F (p) − f (+0).
Док-во. 
 Мы пишем здесь f (+0), а не f (0), так как оригинал может иметь разрыв (первого рода) в точке t = 0.
Мы пишем здесь f (+0), а не f (0), так как оригинал может иметь разрыв (первого рода) в точке t = 0.
Формула дифференцирования оригинала может применяться неоднократно. Если функция-оригинал f (t) имеет производные f ′(t), f ″(t), f ′″(t), f (4)(t), …, f (n)(t), и все они тоже являются оригиналами, имеющими изображения F 1(p), F 2(p), F 3(p), …, Fn (p), то, как только что доказано, f ′(t)  F 1(p) = p F (p) − f (+0). Тогда f ″(t)
F 1(p) = p F (p) − f (+0). Тогда f ″(t)  F 2(p) = p F 1(p) − f ′(+0) = p 2 F (p) − p f (+0) − f ′(+0), f ″′(t)
F 2(p) = p F 1(p) − f ′(+0) = p 2 F (p) − p f (+0) − f ′(+0), f ″′(t)  F 3(p) = p F 2(p) − f ″(+0) = p 3 F (p) − p 2 f (+0) − p f ′(+0) − f ″(+0), …, f (n)(t)
F 3(p) = p F 2(p) − f ″(+0) = p 3 F (p) − p 2 f (+0) − p f ′(+0) − f ″(+0), …, f (n)(t)  Fn (p) = p nF (p) − p n − 1 f (+0) − p n − 2 f ′(+0) − p n − 3 f ″(+0) − … − p f (n − 2)(+0) − f (n − 1)(+0).
Fn (p) = p nF (p) − p n − 1 f (+0) − p n − 2 f ′(+0) − p n − 3 f ″(+0) − … − p f (n − 2)(+0) − f (n − 1)(+0). 
7. Интегрирование изображения. Пусть f (t) - функция-оригинал, f (t)  F (p), и функция
F (p), и функция  ограничена в окрестности точки t = 0. Тогда
ограничена в окрестности точки t = 0. Тогда  тоже является оригиналом и
тоже является оригиналом и 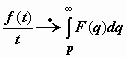 .
.
Док-во. Проинтегрируем равенство  по переменной q = ρ + i η по горизонтальному лучу, проведённому из точки p = ξ + i η, где ξ ≤ ρ = Re q < +∞:
по переменной q = ρ + i η по горизонтальному лучу, проведённому из точки p = ξ + i η, где ξ ≤ ρ = Re q < +∞: 
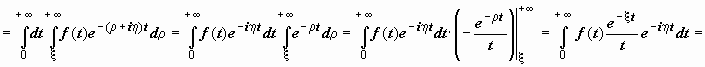
 .
.
Иллюстрации применения теорем об интегрировании изображения и оригинала:
1. Найти изображение интегрального синуса  .
.
Решение: 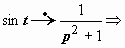 (по теореме 20.2.7)
(по теореме 20.2.7) 

(по теореме 20.2.5)  .
.
2. Найти изображение функции  .
.
Решение. 

 .
.
8. Дифференцирование изображения. Если f (t) - функция-оригинал, и f (t)  F (p), то − t f (t)
F (p), то − t f (t)  F ′(p).
F ′(p).
Док-во.  . Дифференцируя это соотношение по параметру р, получаем
. Дифференцируя это соотношение по параметру р, получаем  .
.
Иллюстрации этого свойства. С его помощью просто получаются изображения степенных функций:  , или
, или  ;
;  , или
, или  ,
,  , или
, или  ;
;  , или
, или  , и вообще
, и вообще  .
.
Другие иллюстрации: 
 , …,
, …,  .
.
 и т.д.
и т.д.
9. Изображение свёртки функций. Теорема Бореля. Интегралы Дюамеля.
Свёртка функций и её свойства.
Определение. Сверткой функций f 1(t) и f 2(t) называется функция  .
.
Свёртка обозначается символом f 1 * f 2: 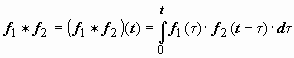 . Если f 1(t) и f 2(t) - функции-оригиналы, то их свёртка - тоже функция-оригинал, показатель роста которой превышает наибольший из показателей роста функций f 1(t) и f 2(t) не больше, чем на 1. Действительно, пусть
. Если f 1(t) и f 2(t) - функции-оригиналы, то их свёртка - тоже функция-оригинал, показатель роста которой превышает наибольший из показателей роста функций f 1(t) и f 2(t) не больше, чем на 1. Действительно, пусть 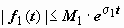 ,
, 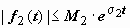 ,
,  , тогда
, тогда 
 , так как t < e t.
, так как t < e t.
Свёртка функций коммутативна: f (t) * g (t) = g (t) * f (t), в этом легко убедиться, заменив в интеграле  переменную τ на τ 1 = t − τ.
переменную τ на τ 1 = t − τ.
Можно показать, что свёртка обладает свойством ассоциативности, т.е. что (f 1 * f 2) * f 3 = f 1 * (f 2 * f 3).
Теорема Бореля (теорема об умножении изображений).  Изображение свёртки двух оригиналов равно произведению изображений свёртываемых оригиналов.
Изображение свёртки двух оригиналов равно произведению изображений свёртываемых оригиналов.
Док-во.  (меняем порядок интегрирования)=
(меняем порядок интегрирования)= 

 .
.
С помощью этой теоремы легко находить оригиналы для изображений вида F 1(p)· F 2(p).
Примеры. Найти оригиналы, если
1.  . Здесь
. Здесь 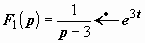 ,
,  , поэтому
, поэтому  .
.
2.  . Здесь
. Здесь  ,
,  , поэтому
, поэтому 
 .
.
3.  . Здесь
. Здесь  , поэтому
, поэтому 
 .
.
Интегралы Дюамеля. Запишем с помощью теоремы Бореля оригиналы для выражения вида pF (p) G (p), где F (p) и G (p) - изображения функций f (t) и g (t). С одной стороны,  (так как, по теореме 20.2.8,
(так как, по теореме 20.2.8,  ); с другой стороны,
); с другой стороны, 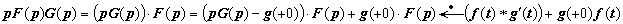 .
.
В развёрнутом виде
 ,
,
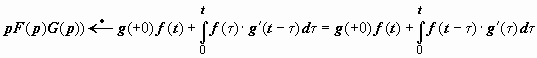 .
.
Каждая из этих формул называется интегралом Дюамеля.
20.3. Таблица стандартных изображений.
Сведём в таблицу полученные ранее изображения элементарных функций.
| f (t) | F (p) | f (t) | F (p) | |||
| 1. | 1 | 
| 9. | e α t · sin β t | 
| |
| 2. | t n | 
| 10. | e α t · cos β t | 
| |
| 3. | e α t | 
| 11. | e α t · sh β t | 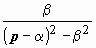
| |
| 4. | e α t · t n | 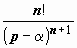
| 12. | e α t · ch β t | 
| |
| 5. | sin β t | 
| 13. | t · sin β t | 
| |
| 6. | cos β t | 
| 14. | t · cos β t | 
| |
| 7. | sh β t | 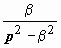
| 15. | t · sh β t | 
| |
| 8. | ch β t | 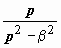
| 16. | t · ch β t | 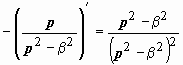
|






