1. Формула Римана-Меллина. Если функция F (p) - изображение функции-оригинала f (t), то f (t) может быть найдена по формуле
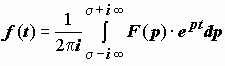 .
.
Это равенство имеет место в каждой точке, в которой f (t) непрерывна. В точках разрыва функции f (t)значение правой части равно  . Интеграл в правой части формулы называют интегралом Меллина; интегрирование может вестись по любой вертикальной прямой p = σ + i ω, σ = const> σ0, − ∞ < ω < ∞, и интеграл понимается в смысле главного значения:
. Интеграл в правой части формулы называют интегралом Меллина; интегрирование может вестись по любой вертикальной прямой p = σ + i ω, σ = const> σ0, − ∞ < ω < ∞, и интеграл понимается в смысле главного значения:  .
.
Вычисление оригинала по формуле Римана-Меллина довольно трудоёмко, поэтому на практике при решении задач применяют другие методы, которые рассматриваются ниже.
2. Элементарный метод нахождения оригинала. Этот метод основан на непосредственном применении таблицы стандартных изображений 20.3 и свойств преобразования Лапласа.
Примеры. 1.  . Представляя изображение в виде
. Представляя изображение в виде 
 и сравнивая эти выражения с формулами 9, 10 таблицы, находим оригинал
и сравнивая эти выражения с формулами 9, 10 таблицы, находим оригинал  .
.
2.  . Наличие степеней переменной р в знаменателе позволяет применить теорему 20.2.5 об интегрировании оригинала:
. Наличие степеней переменной р в знаменателе позволяет применить теорему 20.2.5 об интегрировании оригинала:  ,
,  ,
,  .
.
Можно решить этот пример с помощью свёртки:  ,
, 
 . Однако проще всего представить F (p) в виде суммы простых дробей
. Однако проще всего представить F (p) в виде суммы простых дробей 


 .
.
3. Первая теорема разложения. Если точка p = ∞ является нулём функции F (p), F (p) аналитична в окрестности этой точки и разложение функции по степеням р в окрестности точки p = ∞ имеет вид  , то функция F (p) есть изображение функции
, то функция F (p) есть изображение функции  .
.
Это выражение получается в результате почленного перехода к оригиналам в ряде 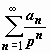 : так как
: так как 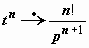 , то
, то 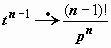 , и
, и  .
.
Примеры. 1.  . Условия теоремы выполнены. Лорановское разложение функции F (p) в окрестности точки p = ∞:
. Условия теоремы выполнены. Лорановское разложение функции F (p) в окрестности точки p = ∞:  .
.
2.  . Здесь
. Здесь  .
.
4. Вторая теорема разложения. Пусть функция F (p) комплексной переменной р аналитична во всей плоскости, за исключением конечного числа изолированных особых точек p 1, p 2, p 3, …, pn, расположенных в полуплоскости Re p < σ0. Если  , и F (p) абсолютно интегрируема вдоль любой вертикальной прямой Re p = σ, σ > σ0, то F (p) является изображением, и
, и F (p) абсолютно интегрируема вдоль любой вертикальной прямой Re p = σ, σ > σ0, то F (p) является изображением, и 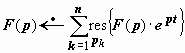 .
.
Док-во. Сведём интеграл в формуле Римана-Меллина  к интегралу по замкнутому контуру. Контур Γ составим из отрезка AB прямой Re p = σ, σ > σ0, и дуги CR окружности | p | = R, расположенной слева от отрезка и содержащей внутри себя все особые точки функции F (p). По основной теореме о вычетах
к интегралу по замкнутому контуру. Контур Γ составим из отрезка AB прямой Re p = σ, σ > σ0, и дуги CR окружности | p | = R, расположенной слева от отрезка и содержащей внутри себя все особые точки функции F (p). По основной теореме о вычетах  .
.  , поэтому
, поэтому 
 . Устремим R → +∞. По лемме Жордана
. Устремим R → +∞. По лемме Жордана  ; а для второго интеграла получаем
; а для второго интеграла получаем  , поэтому в пределе
, поэтому в пределе  .
.
Применим эту теорему для обращения изображения  . Функция F (p) · e pt имеет три особых точки: p = 0 (полюс второго порядка) и
. Функция F (p) · e pt имеет три особых точки: p = 0 (полюс второго порядка) и  (простые полюсы), поэтому
(простые полюсы), поэтому 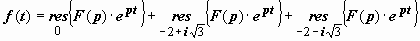 . Находим вычеты:
. Находим вычеты:  ;
; 


 ;
; 
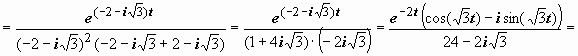

 ;
; 
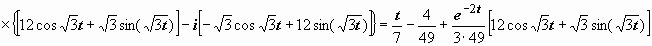 .
.
Если F (p) - несократимая дробно-рациональная функция:  и R m 2 - многочлены соответствующих степеней, и точка p k - полюс порядка ν k, т.е. точка p k - нуль порядка ν k знаменателя R m 2, то
и R m 2 - многочлены соответствующих степеней, и точка p k - полюс порядка ν k, т.е. точка p k - нуль порядка ν k знаменателя R m 2, то  . Производную произведения представим по формуле Лейбница:
. Производную произведения представим по формуле Лейбница: 
 ,
,  , поэтому
, поэтому  .
.
Если все особые точки дробно-рациональной функции F (p) - простые полюса, т.е простые нули знаменателя R m 2, то эта формула существенно упрощается:  , и
, и 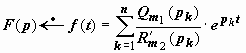 .
.
Пример:  . Здесь знаменатель R 4 (p) = (p − 2)(p + 3)(p 2 + 4) = (p − 2)(p + 3)(p − 2 i)(p + 2 i) = p 4 + p 3 − 2 p 2 + 4 p + 24 имеет только простые нули, R ′4 (p) = 4 p 3 + 3 p 2 − 4 p + 4, поэтому
. Здесь знаменатель R 4 (p) = (p − 2)(p + 3)(p 2 + 4) = (p − 2)(p + 3)(p − 2 i)(p + 2 i) = p 4 + p 3 − 2 p 2 + 4 p + 24 имеет только простые нули, R ′4 (p) = 4 p 3 + 3 p 2 − 4 p + 4, поэтому 


 .
.






