I закон термодинамики позволяет рассчитывать тепловые эффекты различных процессов, но не дает информацию о направлении протекания процесса.
Для протекающих в природе процессов известны две движущие силы:
1. Стремление системы перейти в состояние с наименьшим запасом энергии;
2. Стремление системы к достижению наиболее вероятного состояния, которое характеризуется максимальным количеством независимых частиц.
Первый фактор характеризуется изменением энтальпии. Рассматриваемый случай должен сопровождаться выделением теплоты, следовательно, DH< 0.
Второй фактор определяется температурой и изменением энтропии.
Энтропия(S) - термодинамическая функция состояния системы, которая отражает вероятность реализации того или иного состояния системы в процессе теплообмена.
Как и энергия, энтропия не относится к числу экспериментально определяемых величин. В обратимом процессе, протекающем в изотермических условиях, изменение энтропии можно рассчитать по формуле:
 , ,
| (8) |
из которой видно, что размерность энтропии Дж/К или Дж/(моль×К).
В необратимых процессах выполняется неравенство:
 . .
| (9) |
Это означает, что при необратимом протекании процесса энтропия возрастает благодаря переходу в теплоту части работы.
Таким образом, в обратимых процессах система совершает максимально возможную работу. При необратимом процессе система всегда совершает меньшую работу.
Переход потерянной работы в теплоту является особенностью теплоты как макроскопически неупорядоченной формы передачи энергии. Отсюда возникает трактовка энтропии как меры беспорядка в системе:
При увеличении беспорядка в системе энтропия возрастает и, наоборот, при упорядочиваниии системы энтропия уменьшается.
Так, в процессе испарения воды энтропия увеличивается, в процессе кристаллизации воды - уменьшается. В реакциях разложения энтропия увеличивается, в реакциях соединения - уменьшается.
Физический смысл энтропии установила статистическая термодинамика. Согласно уравнению Больцмана:
 , ,
| (10) |
где k - постоянная Больцмана, равная 1,38×10-23 Дж×К-1,
W - число способов, которыми система может осуществить свое макросостояние. Величину W также называют термодинамической вероятностью.
Статистическая трактовка понятия энтропии означает, что в отличие от энергии, которая присуща каждой отдельной частице, энтропия отражает свойства набора частиц. Отдельная частица энтропией не обладает.
Если обратимый процесс протекает в изобарно-изотермических условиях, то должны выполняться следующие соотношения:

| (11) |
и
 , ,
| (12) |
Таким образом, в обратимом процессе:
 . .
| (13) |
В необратимом процессе выполняется неравенство:
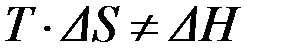 . .
| (14) |
От соотношения величин, стоящих в левой и правой части последнего выражения, зависит направление самопроизвольного протекания процесса.
Если процесс проходит в изобарно-изотермических условиях, то общая движущая сила процесса называется свободной энергией Гиббса или изобарно-изотермическим потенциалом (D G):
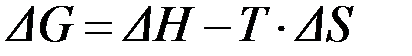 . .
| (15) |
Величина DG позволяет определить направление самопроизвольного протекания процесса:
Если D G < 0, то процесс самопроизвольно протекает в прямом направлении;
Если D G > 0, то процесс самопроизвольно протекает в обратном направлении;
Если D G = 0, то состояние является равновесным.
Пример.
В живых организмах, представляющих собой открытые системы, главным источником энергии для многих биологических реакций - от биосинтеза белка и ионного транспорта до сокращения мышц и электрической активности нервных клеток -является АТФ (аденозин-5¢-трифосфат).
Энергия выделяется при гидролизе АТФ:
АТФ + H2O ⇄ АДФ +H3PO4
где АДФ - аденозин-5¢-дифосфат.
DG0 данной реакции составляет -30 кДж, следовательно процесс протекает самопроизвольно в прямом направлении.
Анализ соотношения энтальпийного и энтропийного факторов в уравнении для расчета изобарно-изотермического потенциала позволяет сделать следующие заключения:
1. При низких температурах преобладает энтальпийный фактор, и самопроизвольно протекают экзотермические процессы;
2. При высоких температурах преобладает энтропийный фактор, и самопроизвольно протекают процессы, сопровождающиеся увеличением энтропии.
На основании изложенного материала можно сформулировать II закон термодинамики:
В изобарно-изотермических условиях в изолированной системе самопроизвольно протекают те процессы, которые сопровождаются увеличением энтропии.
Действительно, в изолированной системе теплообмен невозможен, следовательно, DH = 0 и DG» -T×DS. Отсюда видно, что если величина DS положительна, то величина DG отрицательна и, следовательно, процесс самопроизвольно протекает в прямом направлении.
Другая формулировка II закона термодинамики:
Невозможен некомпенсированный переход теплоты от менее нагретых тел к более нагретым.
В химических процессах изменения энтропии и энергии Гиббса определяют в соответствии с законом Гесса:
 , ,
| (16) |
 . .
| (17) |
Реакции, для которых DG < 0 называют экзэргоническими.
Реакции, для которых DG > 0 называют эндэргоническими.
Величину DG химической реакции можно также определить из соотношения:
D G = D H - T × D S.
В табл. 1 показана возможность (или невозможность) самопроизвольного протекания реакции при различных сочетаниях знаков DH и DS.
Табл. 1. Направление протекания реакций при различных знаках DH и DS.
| Знак изменения функции | Возможность (невозможность) самопроизвольного протекания реакции | Пример реакции | ||
| DH | DS | DG | ||
| - | + | - | Возможно при любых температурах | C6H6 + 7,5O2 = 6CO2 + 3H2O |
| + | - | + | Невозможно при любых температурах | N2 + 2O2 = 2NO2 |
| - | - | ± | Возможно при достаточно низких температурах | 3H2 + N2 = 2NH3 |
| + | + | ± | Возможно при достаточно высоких температурах | N2O4 = 2NO2 |






