мы учимся: во-первых, переформулировать своё суждение другими словами, придавая ему новые оттенки смысла; во-вторых, извлекать из суждения максимум содержащейся в нём информации.
Превращение:
В исходную посылку вставляются два отрицания – перед связкой и перед предикатом.
Ɐ S есть Р суждение типа «А».
Для превращения добавляем одно отрицание (частицу «не») перед связкой «есть»; второе отрицание перед предикатом «Р».
Получается логическая формула: ⱯS не есть не Р - суждение типа «Е»
| S P
есть |
| суждение – «А» | ||||||||||
| Превращение: |
| S не-P
не есть | ||||||||||
Все перелётные птицы имеют крылья 
Ни одна перелётная птица не является не имеющей крыльев.
Ǝ S есть Р суждение типа «I».
Для превращения добавляем одно отрицание (частицу «не») перед связкой «есть»; второе отрицание перед предикатом «Р».
Получается логическая формула: Ǝ S не есть не Р - суждение типа «О»
| S P
(есть) |
| суждение – «I» | |||||||||||
| Превращение: |
|
не есть | |||||||||||
Некоторые слоны являются цирковыми животными 
S P
Некоторые слоны не являются нецирковыми животными
ⱯS не есть Р суждение типа «Е».
Для превращения добавляем одно отрицание (частицу «не») перед связкой «не есть»; второе отрицание перед предикатом «Р».
Если добавить частицу «не» перед связкой «не есть», то двойное отрицание уничтожится и останется связка «есть».
Получается логическая формула: ⱯS не не есть не Р - суждение типа «А»
| S P
не есть
|
| суждение – «Е» | ||||||||||||
| Превращение: |
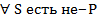
| S не-P
есть
| ||||||||||||
Данные сайты не являются надёжными ресурсами 
Данные сайты являются ненадёжными ресурсами
Ǝ S не есть Р суждение типа «О».
Для превращения добавляем одно отрицание (частицу «не») перед связкой «не есть»; второе отрицание перед предикатом «Р».
Если добавить частицу «не» перед связкой «не есть», то двойное отрицание уничтожится и останется связка «есть».
Получается логическая формула: ƎS не не есть не Р - суждение типа «I»
| S P
(не есть)
|
| суждение – «О» | |||||||||||||
| Превращение: |
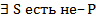
| S не-Р
(есть) | |||||||||||||
Некоторые объекты Солнечной системы не входят в пояс Койпера
Некоторые объекты Солнечной системы являются не входящими в пояс Койпера
Обращение
Субъект и предикат меняются местами по определённым правилам.
Если в исходном суждении предикат не был распределён, то и при обращении, заняв место субъекта он должен быть нераспределённым.
Ɐ S есть Р суждение типа «А».
При обращении меняем местами субъект и предикат. Если предикат в посылке не распределён, то и при обращении будет говориться лишь о части его объёма.
Получается логическая формула: Ǝ Р есть S - суждение типа «I»
| S P
есть |
| суждение – «А» | ||||||||||||
| Обращение: |
| Р S
есть | ||||||||||||
Все перелётные птицы имеют крылья 
Ǝ S есть Р суждение типа «I».
При обращении меняем местами субъект и предикат. Если предикат в посылке не распределён, то и при обращении будет говориться лишь о части его объёма.
Получается логическая формула: Ǝ Р есть S - суждение типа «I»
| S P
(есть) |
| суждение – «I» | ||||||||||||
| Обращение: |
| Р S
есть | ||||||||||||
Некоторые цирковые животные – слоны.
ⱯS не есть Р суждение типа «Е».
При обращении меняем местами субъект и предикат. В общеотрицательном суждении предикат всегда распределён, значит и при обращении мы может говорить обо всём его объёме.
Получается логическая формула: Ɐ Р не есть S - суждение типа «Е»
| S P
не есть
|
| суждение – «Е» | ||||||||||||
| Обращение: |
| Р S
не есть
| ||||||||||||
Надёжными ресурсами не являются данные сайты
Суждения типа «О» обращению не подвергаются. Вывод, который будет получен при обращении частноотрицательного суждения не может быть гарантированно верным.
Противопоставление предикату
Предикат подвергается отрицанию, меняется местами с субъектом,
а связка меняется на противоположную.
Ɐ S есть Р суждение типа «А».
Для противопоставления предикату, предикат отрицаем (добавляем частицу «не») и ставим на место субъекта, связку меняем на противоположную.
Получается логическая формула: Ɐ не Р не есть S - суждение типа «Е»
| S P
есть |
| суждение – «А» | ||||||||||
| Противопос-тавление предикату: |
|
не-Р S
не есть | ||||||||||
Никто из не имеющих крыльев не является перелётной птицей.
ⱯS не есть Р суждение типа «Е».
При противопоставлении предикату предикат отрицаем (добавляем частицу «не» и ставим на место субъекта, связку меняем на противоположную
Получается логическая формула: Ǝ не Р есть S - суждение типа «I»
| S P
не есть
|
| суждение – «Е» | ||||||||||||
| Противопос-тавление предикату: |
| не-Р S
есть | ||||||||||||
Некоторыми ненадёжными ресурсами являются данные сайты.
Ǝ S не есть Р суждение типа «О».
При противопоставлении предикату предикат отрицаем (добавляем частицу «не») и ставим на место субъекта, связку меняем на противоположную
Получается логическая формула: Ǝ не Р есть S - суждение типа «I»
| S P
(не есть)
|
| суждение – «О» | |||||||||||||
| Противо- поставление предикату: | Ǝ неР есть S | не-Р S
(есть) | |||||||||||||
Некоторые не входящие в пояс Койпера (объекты) являются объектами пояса Койпера
Суждения типа «I» противопоставлению предикату не подвергаются. Вывод, полученный из частноутвердительного суждения в этом случае не является гарантированно истинным.
