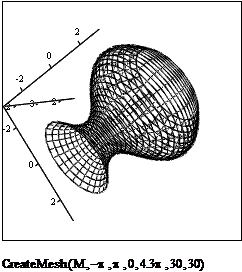
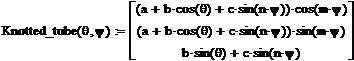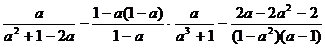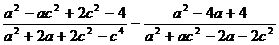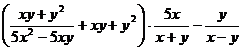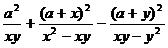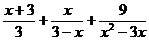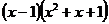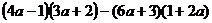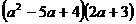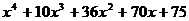Для быстрого построения графика функции двух переменных MathCad использует встроенную функцию CreatMesh.
- Задаем систему параметрических уравнений сферы:
|
|
|
|
|
|
- Объединяем матрицы данных в один массив:
|
|
- Вводим функцию CreateMesh(F,s0,s1,t0,t1,sgrid,tgrid,fmap) в маркер графической области. Она имеет восемь пустых маркеров, в которые последовательно вводится:
- имя матрицы значений или функции F
- начальное значение первой переменной s0
- конечное значение первой переменной s1
- начальное значение второй переменной t0
- конечное значение второй переменной t1
- число линий сетки по первой переменной sgrid
- количество линий сетки по второй переменной tgrid
- карта отображения fmap
|
|
Построение поверхностей вращения
|
|
|
|
|
|
|
|
|
|
|
|
Интересные поверхности
Лента Мебиуса
Лента Мебиуса – это трехмерная неориентируемая фигура с одной границей и стороной. Этим она уникальна и отлична от всех других предметов, которые могут встретиться в повседневной жизни. Ленту Мебиуса также называют листом Мебиуса и поверхностью Мебиуса. Она относится к топологическим объектам, то есть объектам непрерывным. Такие объекты изучает топология - наука, исследующая непрерывность среды и пространства.
Интерес вызывает уже само открытие ленты. Два математика, несвязанных между собой, открыли ее в одном и том же 1858 году. Этими открывателями были Август Фердинанд Мебиус и Иоганн Бенедикт Листинг.
Условно различают ленты по способу сворачивания: по часовой стрелке и против часовой стрелки. Их еще называют правая и левая. Но различить «на глаз» вид ленты невозможно.
Лента Мебиуса имеет характерные свойства:
- Односторонность. Если взять ленту Мебиуса и начать закрашивать в любом ее месте и направлении, то постепенно вся фигура будет закрашена целиком, при этом фигуру не нужно будет переворачивать.
- Непрерывность. Каждую точку этой фигуры можно соединить с другой ее точкой, при этом ни разу не выходя за края ленты.
- Двусвязность (или двумерность). Лента остается цельной, если резать ее вдоль. Из нее не получатся в этом случае две разные фигуры.
- Отсутствие ориентированности. Если представить, что человек мог бы идти по этой фигуре, то при возвращении в точку начала путешествия, он бы превращался в свое отражение.
|
|
|
|
Поверхность Боя
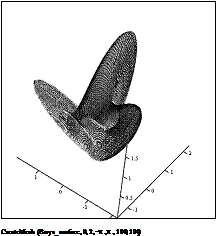Поверхность Боя — типичный представитель класса односторонних поверхностей (к которому, в частности, относится и знаменитая бутылка Клейна), которые невозможно отобразить в трехмерном пространстве без линий самопересечения (без самопересечения такие поверхности можно представить только в четырехмерном пространстве).
|
|
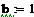
Сплетенная трубка
|
|
|
|
|
|
|
|
|
|
|
|
Ракушка
|
|
|
|
|
|
|
|
|
|
Построение многогранников
Чтобы построить многогранник, следует использовать специальную функцию Polyhedron(S), где S — это либо порядковый номер, либо название, либо код (так называемый Wythoff-символ).
Проще всего можно построить нужный вам многогранник, используя его порядковый номер. Для этого введите соответствующее число в виде строки (то есть его нужно взять в кавычки), поставив перед ним символ номера (#). Учитывая то, что всего встроенных многогранников 80, то и вводимое число должно лежать между 1 и 80.
Задание на лабораторную работу
Вариант задания каждого студента соответствует его порядковому номеру по списку в журнале.
Описать порядок действий (команд), произведенных при решении каждого задания.
Задание 1.3.1
Упростить:
Задание 1.3.2
Разложить выражение:
15. 
16. 
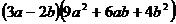
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
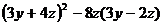
25. 
Задание 1.3.3
Разложить на множители:
Задание 1.3.4
Разложить на простейшие дроби рациональную дробь:
1. 
2. 
3. 
4. 
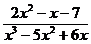
5. 
6. 
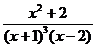
7. 
8. 
9. 
10. 
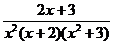
11. 
12. 
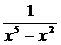
13. 
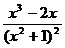
14. 
15. 
16. 
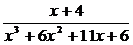
17. 
18. 
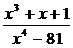
19. 
20. 
21. 
22. 
23. 
24. 
25. 
Задание 1.3.5
Найти:
1. 
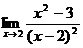
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
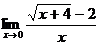
15. 
16. 
17. 
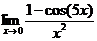
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
Задание 1.3.6
Найти производные функций:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
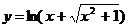
10. 
11. 
12. 
13. 
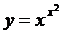
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
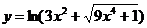
23. 
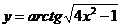
24. 
25. 
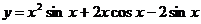
Задание 1.3.7
Найти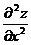 
, 
, 
:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
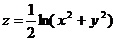
21. 
22. 
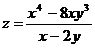
23. 
24. 
25. 
Задание 1.3.8
Найти интеграл:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
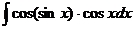
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
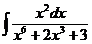
22. 
23. 
24. 
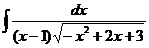
25. 
Задание 1.3.9
Вычислить интеграл:
Задание 1.3.10
Решите уравнение:
1. 
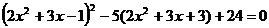
2. 
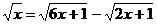
3. 
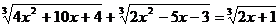
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
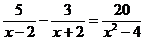
20. 
21. 
22. 
23. 
24. 
25. 
Задание 1.3.11
Решите систему уравнений, используя функцию Find:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
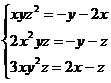
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
Задание 1.3.12
Решите систему уравнений:
- матричным способом и используя функцию lsolve;
- методом Гаусса:
1. 
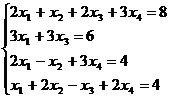
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
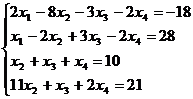
16. 
17. 
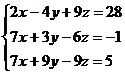
18. 
19. 
20. 
21. 
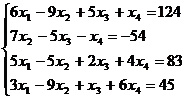
22. 
23. 
24. 
25. 
Задание 1.3.13
Построить график функции:
1. 
2. 
3. 
4. 
5. 
6. 
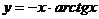
7. 
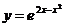
8. 
9. 
10. 
11.
12. 
13. 
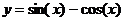
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21.
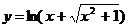
22. 
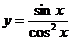
23. 
24. 
25. 
Задание 1.3.14
Построить график поверхности:
1. 
2. 
3. 
4. 
5. 
6. 
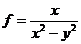
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
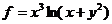
16. 
17. 
18. 
19. 
20. 
21. 
22. 
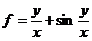
23. 
24. 
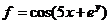
25. 
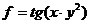
Задание 1.3.1 5
Построить полярный график:
1. 
2. 
3. 
4. 
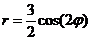
5. 
6. 
7. 
8. 
9. 
10. 
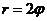
11. 
12. 
13. 
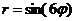
14. 
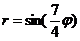
15. 
16. 
17. 
18. 
19. 
20. 
21. 
22. 
23. 
24. 
25. 
1.4 Контрольные вопросы:
1. Назначение Mathcad
2. Основные элементы окна Mathcad
3. Назначение меню Mathcad
4. Назначение панели инструментов Mathcad
5. Назначение панели форматирования Mathcad
6. Назначение математической панели Mathcad
7. Ввод, редактирование и вычисление выражений
8. Использование переменных в Mathcad
9. Создание и использование собственных функций пользователя
10. Переменные с заданным диапазоном изменения значений и переменные с индексами
11. Построение графиков функций
12. Численное дифференцирование и интегрирование функций.
13. Решение уравнений
