Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных x1, x2,…,xn.
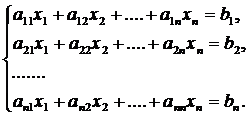 (1)
(1)
В соответствии с правилом умножения матриц рассмотренная система линейных уравнений может быть записана в виде:  , где:
, где:
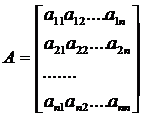
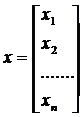
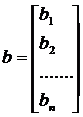
Если определитель матрицы А не равен 0, то система имеет единственное решение, т.к. существует обратная матрица А-1 при умножении обеих частей уравнения на которую получаем:
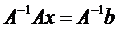

Системы линейных уравнений удобно решать с помощью функции lsolve:
lsolve(А, b)- возвращается вектор решения x такой, что  (см. рис. 9).
(см. рис. 9).

Рис.9.
Метод Гаусса
Метод Гаусса состоит в том, что систему (1) приводят последовательным исключение неизвестных к эквивалентной системе с треугольной матрицей:

решение которой находят по рекуррентным формулам:
 ,
, 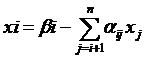

В матричной записи это означает, что сначала (прямой ход метода Гаусса) элементарными операциями над строками приводят расширенную матрицу системы к ступенчатому виду:
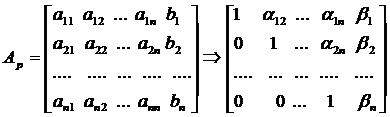
а затем (обратный ход метода Гаусса) эту ступенчатую матрицу преобразуют так, чтобы в первых n столбцах получилась единичная матрица:
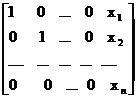
Последний, (n+1) этой матрицы содержит решение системы (1).
В Mathcad прямой и обратный ходы метода Гаусса выполняет функция rref(A). На рис.10 показано решение системы линейных уравнений методом Гаусса, в котором используются следующие функции:

Рис. 10
rref(A) - возвращает ступенчатую форму матрицы А.
augment(A, В) - возвращает матрицу, сформированную слиянием матриц-аргументов слева направо. Массивы A и В должны иметь одинаковое число строк.
submatrix(A, ir, jr, ic, jc) - возвращает матрицу, состоящую из всех элементов с ir по jr строкуи столбцах с ic по jc. Удостоверьтесь, что ir ≤ jr и ic ≤ jc, иначе порядок строк и (или) столбцов будет обращен.
При работе с массивами следует уметь обращаться с системной переменной ORIGIN. Если в тексте документа она не упоминается, то её значение по умолчанию считается равным нулю и нумерация элементов в массиве начинается с нулевого элемента, как в языке Си. При желании можно начать нумерацию с единицы. Для этого следует ввести оператор ORIGIN:=1.
Создание графиков
В Mathcad встроено несколько различных типов графиков, которые можно разбить на две большие группы:
Ø Двумерные графики
- XY (декартовый) график,
- полярный график;
Ø Трехмерные графики
- график трехмерной поверхности,
- график линий уровня,
- трехмерная гистограмма,
- трехмерное множество точек,
- векторное поле.






