Среда моделирования MATLAB может весьма эффективно использоваться для того, чтобы раскрыть важность объединения фундаментального знания с современными информационными технологиями, с целью освоения практического приложения полученных теоретических основ.
Пакет прикладных программ (ППП) ControlSystemToolbox (CST), посвящённый проблемам изучения, построения и анализа систем управления, призван открыть инновационные и высокотехнологичные возможности как для студентов и учёных-исследователей, вовлечённых в круг задач проектирования технических систем, так и для специалистов крупных компаний различных отраслей, в повседневной деятельности обращающихся к высокопроизводительным вычислениям и обработке больших информационных массивов.
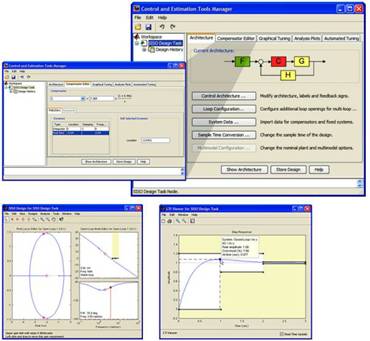
Рис. 1. Графический интерфейс и возможности пакета ControlSystemToolbox.
При реализации пакета использованы принципы объектно-ориентированного программирования, введён новый класс объектов: линейные системы с постоянными параметрами (lineartimeinvariantobjects, или lti -объекты). Этот класс включает линейныенепрерывные или дискретные, одномерные с одним входом и одним выходом (SISO-системы) и многомерные с несколькими входами и несколькими выходами (MIMO-системы).
В CSTвведён ряд функций, позволяющих определять динамические параметры системы: нули и полюсы, собственные частоты и коэффициенты демпфирования. Специализированный функционал позволяет рассчитывать и строить переходные функции и частотные характеристики систем (рис. 1).
ППП ControlSystemToolbox позволяет решать также и задачи синтеза регуляторов для линейных систем автоматического управления с постоянными параметрами. В пакет встроен ряд функций и процедур для синтеза регулятора на основе желаемого расположения полюсов или обеспечения минимального значения квадратичного критерия качества (ЛК-регулятор), синтеза наблюдателя и фильтра Калмана для оценки переменных состояния системы по известным значениям входных и результирующих векторов.
Для описания непрерывных и дискретных динамических моделей систем управления с постоянными параметрами CST использует одну из следующих функциональных форм:
1) tf-форму передаточной функции;
2) zpk-форму нулей, полюсов и обобщённого коэффициента передачи;
3) ss-форму пространства состояний.
Математическую модель стационарной непрерывной или дискретной системы можно задать следующими способами:
1) tf-форме передаточной функции:

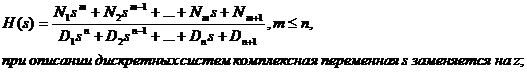
2) в zpk-форме нулей, полюсов и коэффициента усиления:
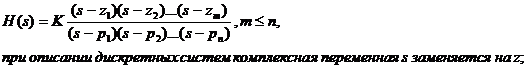
3) в ss-форме пространства состояний в виде системы дифференциальных уравнений:

ППП ControlSystemToolbox обеспечивает генерацию структур данных для каждой из моделей, называемых соответственно tf-, zpk- или ss- подклассами класса lti-объектов. Эти три подкласса могут быть описаны одним типом данных – массивом ячеек, что позволяет манипулировать линейными системами как единым объектом, а не наборами данных в виде векторов или матриц. Например, команда P=tf([1 2],[1 1 10]) создаёт объект подкласса tf с передаточной функцией

Так, можно манипулировать этой передаточной функцией как стандартным объектом lti-класса, к примеру, построить логарифмические частотные характеристики (диаграмма Боде) с помощью команды bode (P).
Задание №1.
С помощью командного обеспечения ControlSystemToolbox задайте следующую передаточную функцию:
| Вариант 1 | 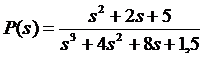
|
| Вариант 2 | 
|
| Вариант 3 | 
|
Постройте диаграмму Боде, переходную характеристику, попробуйте извлечь информацию о числителе и знаменателе. Постройте дискретную модель непрерывной системы с помощью команды SysD = c 2 d (SysC, Ts), где SysC –непрерывнаясистема с периодом дискретности Ts.
Средствами функции step (H,’ g -’, Hd,’ r -’) отобразите полученные переходные процессы, где H–непрерывная система, а Hd–дискретный вариантрассмотрения.
Поэкспериментируйте с вычислением передаточной функции для заданного значения аргумента. Используйте команду frsp = evalfr (sys, w), где sys – передаточная функция lti -модели, а w – заданный аргумент. В нашем случае w =1+ j.
Задание №2.
Сформируйте модель zpk-формы. Для этого введите функцию вида:
h = zpk (0, [1- i 1+ i 2], -2).
Внимательно посмотрите на ответную информацию Matlabв командном окне. Какими параметрами объясняется характеристика заданной функции? Каким образом можно математически (в форме отношения) представить соответствующую функцию?
Задание №3.
Исследуйте основы описания динамических систем в пространстве состояний. В качестве примера представлена простая модель электрического двигателя (рис. 2), которой соответствует дифференциальное уравнение 2-ого порядка:


Рис. 2. Схематичное представление электрического двигателя и его составляющих.
Этому дифференциальному уравнению можно поставить в соответствие следующую систему уравнений, используя в качестве переменных состояния угол и угловую скорость вращения ротора:

Cоздайте соответствующую ss -модель (вышеприведённая система записана в явной форме Коши):
sys = ss (A, B, C, D).
Проанализируйте отклик Matlabв командной строке после формирования ss-модели. Чем будет отличаться форма модели при применении функции dss (A, B, C, D, E)?
** *
Введение ввозможности Simulink
Фундаментальное инструментальное приложение Simulink пакета Matlab предоставляет широкий диапазон возможностей по структурной композиции, детальному изучению и анализу систем управления любой сложности. Непосредственно процесс цифровой обработки сигналов, поступающих с исследуемых элементов системы, доступен для практической реализации и определения целевых параметров и функциональных зависимостей.
Формирование сигналов в Simulink осуществляется при помощи блоков генерации сигналов раздела Sources библиотеки (рис. 3):

Рис. 3. Библиотека блоков источников сигналаSources.
Библиотека представлена блоками генерации сигналов различного происхождения, среди которых:
Band-Limited White Noise – генератор нормального белого шума с равномерной финитной спектральной плотностью мощности и заданным временем корреляции для аналоговых систем;
Constant – источник постоянного сигнала;
Pulse Generator – генератор периодических прямоугольных импульсов;
Random Number – генератор нормального белого шума с заданным математическим ожиданием и дисперсией;
Signal Generator – генератор сигналов: гармонического, трапецеидального, пилообразного и случайного;
Sine Wave – генератор гармонического сигнала;
Step – генератор ступенчатого воздействия;
Uniform Random Number – генератор равномерного белого шума с заданным максимальным и минимальным значениями случайной величины.
Блоки библиотеки Sinks позволяют визуализировать результаты моделирования, среди которых:
Display – блок отображения численных значений сигналов;
Out – выходной порт для сигналов подсистем;
Scope – осциллограф;
Floating Scope – блок осциллографа, способного в процессе моделирования подключаться к различным сигналам;
Terminator – нагрузка для неиспользуемых сигналов;
To File – экспорт сигнала в mat- файл;
To Workspace – экспортсигналав Workspace;
XY Graph – двухкоординатный осциллограф.
Функциональное управление взаимодействием информационных потоков осуществляют блоки математических операций из раздела Math Operations:
Abs – блок взятия модуля сигнала;
Add – блок матричного или поэлементного сложения;
Bias – блок добавления постоянной составляющей к входному сигналу;
Gain – блок поэлементного или матричного умножения на коэффициент;
Math Function – блок вычисления математической функции (экспонента, логарифм, возведение в степень и др.);
Product – блок выполнения матричного или поэлементного умножения;
Sign – блок вычисления знака входного сигнала;
Substract – блок матричного или поэлементного вычитания;
Sum – блок матричного или поэлементного сложения.
Для того чтобы назначать верные «маршруты» сигналам (т.е. направлять информационные потоки), в библиотеке Simulink есть раздел «SignalRouting» (рис. 4):

Рис. 4. Средства маршрутизации сигналов в Simulink.
Блоки библиотеки SignalRouting необходимы для обеспечения разного рода трансферных операций с сигналами: переключения сигналов, объединение сигналов в шину, «разводку» сигналов из шины и других. Наиболее часто используемые блоки SignalRouting:
Bus Creator – объединение различных сигналов в шины;
Mux – объединение скалярных сигналов в векторный сигнал;
Demux – выделение из векторного сигнала скаляров и/или векторов;
Goto – блок беспроводной передачи сигналов к From;
From – блок приема сигналов от Goto;
Switch – автоматический переключатель сигналов.
Вышеперечисленные и исследуемые далее блоки, объединяемые в звенья разной структуры, позволяют воспроизводить модели сложных систем автоматического управления, а затем моделировать их поведение в реальном времени, задавая на входе разные значения.
Приложение Simulink содержит многогранный прикладной диапазон инструментариев (Toolboxes), доступ к которым открывается после перечисления стандартных блоков SimulinkLibraryBrowser. Широкий выбор инструментальных функциональных блоков позволяет, например, производить цифровую обработку сигналов (SignalProcessingBlockset), управление с прогнозирующей моделью (ModelPredictiveControlToolbox), моделирование с помощью нейронных сетей (NeuralNetworkToolbox), использовать элементы нечёткой логики при построении систем (FuzzyLogicToolbox).
Задание 4.
Постройтеs-модель (сохраните её под именем “ LR 2_< your _ name >_ FirstModel. mdl ”), демонстрирующую примеры отображения сигналов вида, соответствующего вашему варианту (исходный и шумовая составляющая). Сигналы поступают с блоков соответствующих источников (согласно рис. 5). Для того чтобы задать количество входных портов для осциллографа (Scope), необходимо на панели инструментов этого блока (предварительно активируя его на схеме двойным щелчком ЛКМ[1]) найти значок «Parameters» (обычно второй слева) и открыть диалоговое окно, затем во вкладке General указать соответствующий параметр «NumberofAxes» (в нашем варианте равный двум). Запуск процесса моделирования осуществим с помощью значка «Start»  на панели инструментов, напоминающего кнопку «Play» (либо активируя пункты меню Simulation → Start). Отобразить экран осциллографа возможно двойным щелчком ЛКМ по области этого элемента на схеме:
на панели инструментов, напоминающего кнопку «Play» (либо активируя пункты меню Simulation → Start). Отобразить экран осциллографа возможно двойным щелчком ЛКМ по области этого элемента на схеме:
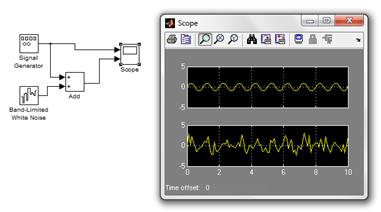
Рис. 5. Пример представления схемы s-модели, учитывая изменения в значении числа портов осциллографа.
Применим маршрутизацию (блок Mux) к исходным данным для наглядной характеристики и сравнения начального и зашумленного сигналов (рис. 6):

Рис. 6. Пример представления схемы s-модели с маршрутизацией сигналов.
| № варианта | Источник сигнала | Шумовой элемент |
| Вариант 1 | Sine Wave | Band-Limited White Noise |
| Вариант 2 | Signal Generator | Random Number |
| Вариант 3 | Step | Uniform Random Number |
Как Вы думаете, каким образом можно увеличить амплитуду исходного сигнала? Изменениекакого параметраповлияет на период наблюдения за динамикой системы? Какой параметр в одном из блоков схемы необходимо изменить, чтобы рассмотреть ещё два дополнительных цифровых сигнала, поступающих с источников PulseGenerator и CounterFree-running?
Отчёт по работе содержит:
1) последовательное выполнение каждого из заданий, комментарии;
2) графические отображения результатов экспериментов;
3) анализ и основные выводы по применению функционала пакетов ControlSystemToolboxи Simulink, включая ответы на поставленные вопросы.
1Здесь и далее: ЛКМ - левая кнопка мыши; ПКМ – правая кнопка мыши соответственно.






