Лабораторная работа № 1
Исследование разомкнутой линейной системы при случайных возмущениях (краткие теоретические сведения)
Оценка корреляционной функции
В прикладных задачах часто нужно определить корреляционную функцию и спектральную плотность по экспериментальным данным. При этом мы можем наблюдать и анализировать только «кусок» реализации на временном интервале от нуля до некоторого  , поэтому для невозможно использовать усреднение по ансамблю. Остается надеяться на то, что процесс эргодический, и применять усреднение по времени.
, поэтому для невозможно использовать усреднение по ансамблю. Остается надеяться на то, что процесс эргодический, и применять усреднение по времени.
Пусть известна реализация случайного процесса  на интервале от 0 до
на интервале от 0 до  . Для оценки (приближенного вычисления) корреляционной функции при
. Для оценки (приближенного вычисления) корреляционной функции при  (то есть при положительных
(то есть при положительных  , достаточно малых по сравнению с
, достаточно малых по сравнению с  ) можно использовать формулу
) можно использовать формулу
 .
. 
(3)
Обратите внимание, что время усреднения равно  , а не
, а не  , потому что только интервал
, потому что только интервал  содержит как
содержит как 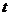 , так и
, так и  . К сожалению, точно вычислить этот интеграл невозможно, потому что мы не знаем математическую формулу для
. К сожалению, точно вычислить этот интеграл невозможно, потому что мы не знаем математическую формулу для  . В реальности обычно известны только значения этой функции (выборка) в моменты
. В реальности обычно известны только значения этой функции (выборка) в моменты  , где
, где  – интервал между измерениями. Тогда
– интервал между измерениями. Тогда 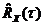 можно приближенно подсчитать только для
можно приближенно подсчитать только для  (где
(где  ) по формуле
) по формуле
 ,
,  ,
,
в которой интеграл заменен на сумму. С теоретической точки зрения математическое ожидание такой оценки (при усреднении по ансамблю) совпадает с истинной корреляционной функцией, то есть это – несмещенная оценка.
Оценка спектральной плотности
Использование оценки корреляционной функции
Предположим, что мы исследуем эргодический процесс и знаем одну реализацию  на интервале от 0 до некоторого
на интервале от 0 до некоторого  . Выше было показано, что по этим данным можно построить оценку корреляционной функции. Если бы мы знали полностью непрерывную корреляционную функцию
. Выше было показано, что по этим данным можно построить оценку корреляционной функции. Если бы мы знали полностью непрерывную корреляционную функцию  , для оценки спектральной плотности можно было бы использовать преобразование Фурье (формулу (2)):
, для оценки спектральной плотности можно было бы использовать преобразование Фурье (формулу (2)):
 .
.
В реальности известны лишь значения  в отдельных точках, поэтому последнюю формулу нужно перевести в дискретный вид, заменив интеграл на конечную сумму:
в отдельных точках, поэтому последнюю формулу нужно перевести в дискретный вид, заменив интеграл на конечную сумму:

 .
.
(4)
Этот метод оценки спектральной плотности называют методом Блэкмана-Тьюки.
К сожалению, такой подход не всегда дает удовлетворительные результаты. Дело в том, что мы знаем только часть корреляционной функции, для значений  от 0 до
от 0 до  . Эта неполнота знаний может очень существенно влиять на результаты оценки спектра, вплоть до того, что вычисления по формуле (4) могут дать для некоторых частот отрицательные значения спектральной плотность. Этого не может быть в принципе, потому что мощность сигнала (и любой его составляющей) не может быть отрицательной.
. Эта неполнота знаний может очень существенно влиять на результаты оценки спектра, вплоть до того, что вычисления по формуле (4) могут дать для некоторых частот отрицательные значения спектральной плотность. Этого не может быть в принципе, потому что мощность сигнала (и любой его составляющей) не может быть отрицательной.
Окна
Чтобы исправить ситуацию, нужно как-то «сгладить» незнание корреляционной функции при больших  и сделать оценку спектральной плотности более надежной. Для этого используются так называемые «окна» – четные функции, на которые умножается корреляционная функция перед тем, как применить к ней преобразование Фурье. Одно из простейших «окон» – окно Хэмминга:
и сделать оценку спектральной плотности более надежной. Для этого используются так называемые «окна» – четные функции, на которые умножается корреляционная функция перед тем, как применить к ней преобразование Фурье. Одно из простейших «окон» – окно Хэмминга:
 .
.
На рисунке слева показано окно Хэмминга, а справа – исходная оценка корреляционной функции 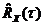 и результат применения к ней окна Хэмминга
и результат применения к ней окна Хэмминга  (красная линия):
(красная линия):

| 
|
Ясно видно, что применение этого окна (и других тоже) практически не изменяет форму корреляционной функции при малых  , но сглаживает все выбросы при больших
, но сглаживает все выбросы при больших  , которые, скорее всего, вызваны случайными ошибками.
, которые, скорее всего, вызваны случайными ошибками.
Для оценки спектральной плотности с учетом окна  применяют формулу, аналогичную (4):
применяют формулу, аналогичную (4):

 .
.
(5)
Не стоит печалиться по поводу того, что окно вносит дополнительное искажение. Так или иначе, «окно» используется всегда. Фактически, усекая корреляционную функцию, мы применяем прямоугольное окно:
 .
.
На следующем рисунке показаны оценки спектра сигнала, полученные при использовании прямоугольного окна ( , синяя линия) и окна Хэмминга (
, синяя линия) и окна Хэмминга ( , красная линия).
, красная линия).

|
Хорошо видно, что график  заходит в отрицательную область, что невозможно с физической точки зрения. Применение окна Хэмминга позволило избавиться от этой проблемы и сгладить скачкообразные изменения оценки спектра.
заходит в отрицательную область, что невозможно с физической точки зрения. Применение окна Хэмминга позволило избавиться от этой проблемы и сгладить скачкообразные изменения оценки спектра.






