Цифровым логическим элементом (LogicGate) называется физическое устройство, реализующее одну из операций алгебры логики или простую логическую функцию. Схема, составленная из конечного числа логических элементов по определенным правилам, называется логической схемой.
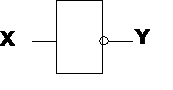
Основными логическими элементами являются: конъюнкция (И), дизъюнкция (ИЛИ), отрицание (НЕ). Условные графические обозначения этих логических элементов приведены на рис.12.


а) б) в)
Рис.12– Условное графическое обозначение логических элементов:а) – И; б) – ИЛИ; в) – НЕ
Описание работы логических элементов и логических схем может быть представлено различными способами:
1. Алгебраическое выражение, например, 
2. Таблица истинности, например, табл.2.2 для функции И.
Табл.2.2
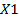
| 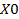
| 
|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
3. Временная диаграмма состояний входных и выходных сигналов, например, рис.13 для функции И.

Рис.13– Временная диаграмма состояний логического элемента И
Из булевой алгебры известен принцип двойственности логических операций, заключающийся в их взаимном преобразовании, например, если в условии, определяющем операцию И, значения всех переменных и самой функции заменить инверсией, а знак конъюнкции – знаком дизъюнкции, получится условие, определяющее операцию ИЛИ, т.е.
если 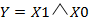 , то , то  . .
| (8) |
Справедливо и обратное преобразование:
если  , то , то  . .
| (9) |
Важным практическим следствием принципа двойственности является тот факт, что при записи логических выражений и, следовательно, построении логических схем, можно обойтись только двумя типами операций, например, операциями И и НЕ или ИЛИ и НЕ. В связи с этим можно ввести понятие функционально полной системы логических элементов – совокупность логических элементов, позволяющих реализовать логическую схему произвольной сложности. Таким образом, системы двух элементов И и НЕ, ИЛИ и НЕ наравне с системой из трех элементов И, ИЛИ, НЕ являются функционально полными.
На практике широкое применение нашли логические элементы, совмещающие функции элементов указанных выше функционально полных систем. Это элементы И-НЕ и ИЛИ-НЕ, которые носят названия соответственно штрих Шеффера и стрелка Пирса. По определению каждый из этих элементов также образует функционально полную систему. Их условные графические обозначения приведены на рис.14.

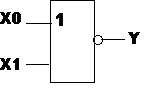
а) б)
Рис.14– Условное графическое обозначение логических элементов:а) – И-НЕ; б) – ИЛИ-НЕ
При разработке логических схем может оказаться, что логический элемент имеет больше входов, чем число переменных, входящих в реализуемую с их помощью логическую функцию. При этом необходимо решить вопрос о том, как следует подключать свободные входы. Для рассмотрения этого случая вводится понятие активного и пассивного логических уровней.
Активным логическим уровнем называется такое значение входной переменной, которое однозначно определяет выходной сигнал логического элемента. Например, для логического элемента И активным логическим уровнем является сигнал лог.0, так как его наличие хотя бы на одном из n-входов этого элемента однозначно определяет получение на выходе сигнала лог.0. Пассивным логическим уровнем для элемента И будет соответственно сигнал лог.1.
Для уменьшения фактического числа входов логического элемента можно на неиспользуемые входы подавать сигналы пассивного уровня. В рассмотренном случае для элемента И – сигнал лог.1.
Другой прием уменьшения фактического числа входов логического элемента основан на теоремах алгебры логики ( – на несколько входов логического элемента можно подавать одну и ту же логическую переменную, т.е. объединять свободные входы с уже задействованными.
– на несколько входов логического элемента можно подавать одну и ту же логическую переменную, т.е. объединять свободные входы с уже задействованными.
В табл.3 представлены основные логические элементы, их обозначения, схемы и выполняемые функции.
Табл.3 – Основные логические элементы
| Элемент | Обозначение | Схема | Функция |
| НЕ | ЛН |

|
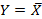
|
| И | ЛИ |

|
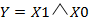
|
| И-НЕ | ЛА |

|

|
| ИЛИ | ЛЛ |

|

|
| ИЛИ-НЕ | ЛЕ |
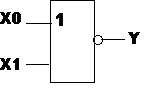
|
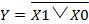
|
| Исключающее ИЛИ | ЛП |

|

|
Порядок выполнения работы
1. Ознакомиться с методическими указаниями к лабораторной работе.
2. По табл.4 выбрать задание, которое заключается в описании работы устройства, предназначенного для реализации.
Табл.4 – Варианты заданий
| № варианта | Описание |
| 1 | Устройство имеет пять входов. На его выходе устанавливается уровень лог.1. тогда, когда более чем на трех входах имеются единицы |
| 2 | Устройство имеет пять входов. На его выходе устанавливается уровень лог.1. тогда, когда не более чем на трех входах имеются единицы |
| 3 | Устройство имеет пять входов. На его выходе устанавливается уровень лог.0. тогда, когда более чем на трех входах имеются нули |
| 4 | Устройство имеет пять входов. На его выходе устанавливается уровень лог.0. тогда, когда не более чем на трех входах имеются нули |
| 5 | Устройство имеет пять входов. На его выходе устанавливается уровень лог.1. тогда, когда более чем на трех входах имеются нули |
| 6 | Устройство имеет пять входов. На его выходе устанавливается уровень лог.1. тогда, когда не более чем на трех входах имеются нули |
| 7 | Устройство имеет пять входов. На его выходе устанавливается уровень лог.0. тогда, когда более чем на трех входах имеются единицы |
| 8 | Устройство имеет пять входов. На его выходе устанавливается уровень лог.0. тогда, когда не более чем на трех входах имеются единицы |
3. По заданному описанию составить таблицу истинности.
4. По таблице истинности построить каноническую таблицу.
5. По канонической таблице построить структурную таблицу.
6. Структурную таблицу привести к модифицированному виду.
7. По виду структурной таблицы реализовать структурную схему на коммутаторах К2-1 или К1-2.
8. Произвести необходимые упрощения структурной схемы.
9. Построить логическую схему устройства.
10. Составить отчет по лабораторной работе.
Содержание отчета
Отчет должен содержать:
1. Титульный лист.
2. Цель работы.
3. Построенные:
- таблицу истинности;
- каноническую таблицу;
- структурную таблицу;
- модифицированную структурную таблицу;
- структурную схему устройства;
- упрощенную структурную схему;
- логическую схему устройства.
4. Вывод.
Контрольные вопросы
1. Что такое логическая переменная и логический сигнал? Какие значения они могут принимать?
2. Что такое логическая функция?
3. Назовите основные операции булевой алгебры.
4. Что такое таблица истинности. Приведите пример.
5. Что такое функционально полная система логических элементов?
6. Какие логические элементы составляют базовый набор?
7. Приведите условное обозначение логических элементов НЕ, И, И-НЕ, ИЛИ, ИЛИ-НЕ, Исключающее ИЛИ.






