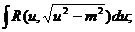Лагранжа или формулой конечных приращений. 4 страница

                                                                0

Таким образом 3x³ – 4x² – 17x + 6 = (x – 3)(3x² + 5x – 2) = (x – 3)(x + 2)(3x – 1). Тогда:

 

 

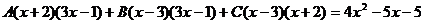
Для того, чтобы избежать при нахождении неопределенных коэффициентов раскрытия скобок, группировки и решения системы уравнений (которая в некоторых случаях может оказаться достаточно большой) применяют так называемый метод произвольных значений. Суть метода состоит в том, что в полученное выше выражение подставляются поочередно несколько (по числу неопределенных коэффициентов) произвольных значений х. Для упрощения вычислений принято в качестве произвольных значений принимать точки, при которых знаменатель дроби равен нулю, т.е. в нашем случае – 3, -2, 1/3. Получаем:

   

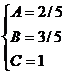
Окончательно получаем:

 

 =

 

 

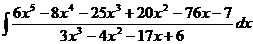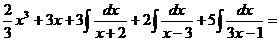
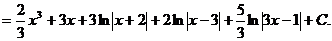
       Пример.

Найдем неопределенные коэффициенты:

 

 

                         

 

                                

 

 

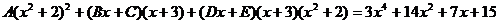
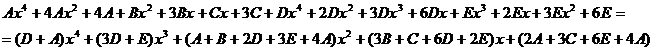
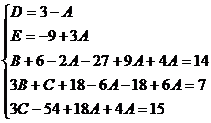
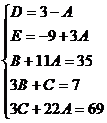
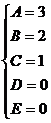
Тогда значение заданного интеграла:

 

 

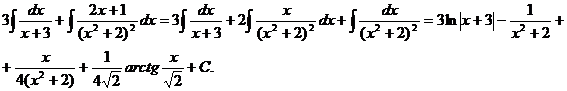
Интегрирование некоторых тригонометрических

функций.

 

       Интегралов от тригонометрических функций может быть бесконечно много. Большинство из этих интегралов вообще нельзя вычислить аналитически, поэтому рассмотрим некоторые главнейшие типы функций, которые могут быть проинтегрированы всегда.

 

 

Интеграл вида .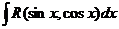

 

       Здесь R – обозначение некоторой рациональной функции от переменных sinx и cosx.

Интегралы этого вида вычисляются с помощью подстановки . Эта подстановка позволяет преобразовать тригонометрическую функцию в рациональную.

,       

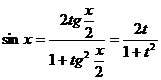Тогда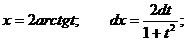

Таким образом:

Описанное выше преобразование называется универсальной тригонометрической подстановкой.

 

       Пример.

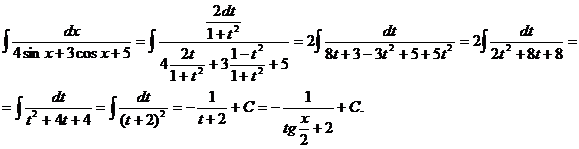
       Несомненным достоинством этой подстановки является то, что с ее помощью всегда можно преобразовать тригонометрическую функцию в рациональную и вычислить соответствующий интеграл. К недостаткам можно отнести то, что при преобразовании может получиться достаточно сложная рациональная функция, интегрирование которой займет много времени и сил.

       Однако при невозможности применить более рациональную замену переменной этот метод является единственно результативным.

 

       Пример.

 

 

Интеграл вида 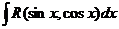   если

функция R является нечетной относительно cosx.

 

Несмотря на возможность вычисления такого интеграла с помощью универсальной тригонометрической подстановки, рациональнее применить подстановку t = sinx.

      

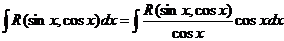
Функция 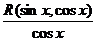 может содержать cosx только в четных степенях, а следовательно, может быть преобразована в рациональную функцию относительно sinx.

 

       Пример.

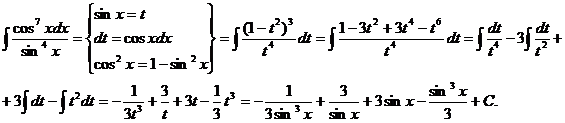
       Вообще говоря, для применения этого метода необходима только нечетность функции относительно косинуса, а степень синуса, входящего в функцию может быть любой, как целой, так и дробной.

 

Интеграл вида 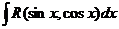   если

функция R является нечетной относительно sinx.

 

       По аналогии с рассмотренным выше случаем делается подстановка t = cosx.

Тогда

 

 

       Пример.

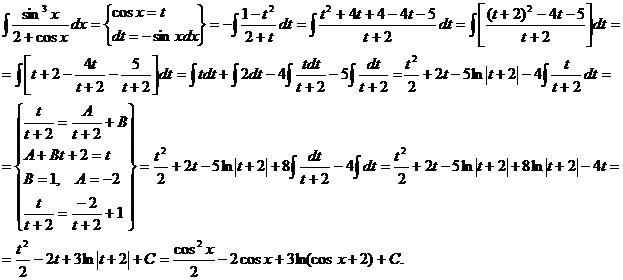
Интеграл вида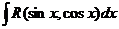

функция R четная относительно sinx и cosx.

 

       Для преобразования функции R в рациональную используется подстановка

t = tgx.

Тогда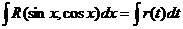

 

       Пример.

 

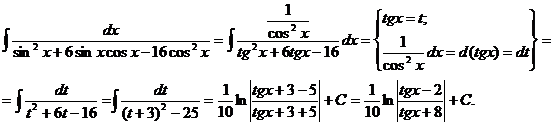
Интеграл произведения синусов и косинусов

различных аргументов.

 

В зависимости от типа произведения применятся одна из трех формул:

 

 

 

 

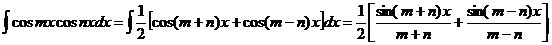
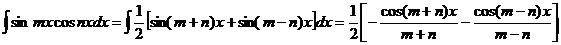
       Пример.

 

       Пример.

 

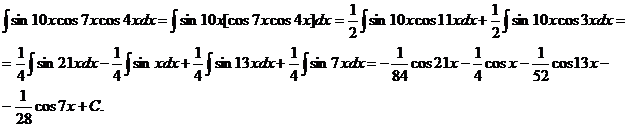
       Иногда при интегрировании тригонометрических функций удобно использовать общеизвестные тригонометрические формулы для понижения порядка функций.

 

       Пример.

 

 

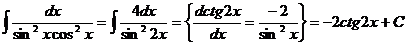
       Пример.

 

 

       Иногда применяются некоторые нестандартные приемы.

 

       Пример.

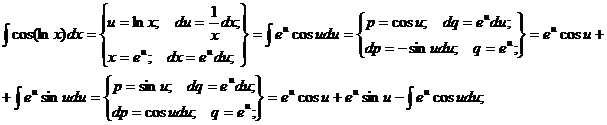
Итого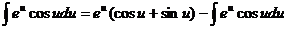

              

 

 

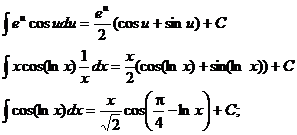
Интегрирование некоторых иррациональных функций.

Далеко не каждая иррациональная функция может иметь интеграл, выраженный элементарными функциями. Для нахождения интеграла от иррациональной функции следует применить подстановку, которая позволит преобразовать функцию в рациональную, интеграл от которой может быть найден как известно всегда.

Рассмотрим некоторые приемы для интегрирования различных типов иррациональных функций.

 

Интеграл вида 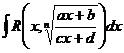где n- натуральное число.

 

       С помощью подстановки  функция рационализируется.

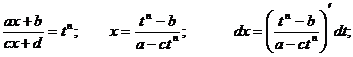
Тогда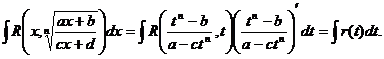

 

 

       Пример.

 

 

 

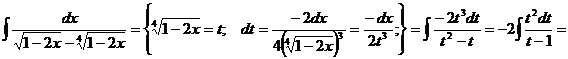
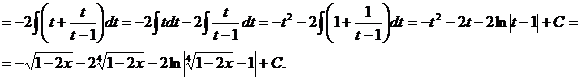
       Если в состав иррациональной функции входят корни различных степеней, то в качестве новой переменной рационально взять корень степени, равной наименьшему общему кратному степеней корней, входящих в выражение.

       Проиллюстрируем это на примере.

 

       Пример.

 

 

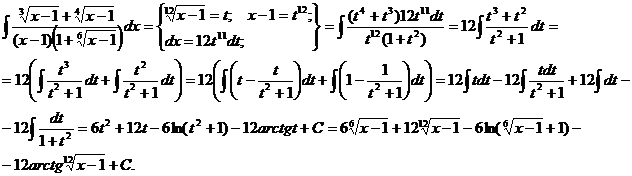
Интегрирование биноминальных дифференциалов.

 

       Определение: Биноминальным дифференциалом называется выражение

x^m(a + bxⁿ) ^p dx

где m, n, и p – рациональные числа.

 

       Как было доказано академиком Чебышевым П.Л. (1821-1894), интеграл от биноминального дифференциала может быть выражен через элементарные функции только в следующих трех случаях:

 

1) Если р – целое число, то интеграл рационализируется с помощью подстановки

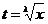, где l - общий знаменатель m и n.

 

2) Если 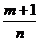  - целое число, то интеграл рационализируется подстановкой

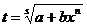, где s – знаменатель числа р.

 

 

3) Если 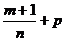 - целое число, то используется подстановка 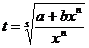, где s – знаменатель числа р.

 

       Однако, наибольшее практическое значение имеют интегралы от функций, рациональных относительно аргумента и квадратного корня из квадратного трехчлена.

       На рассмотрении этих интегралов остановимся более подробно.

 

 

Интегралы вида .

 

       Существует несколько способов интегрирования такого рода функций. В зависимости от вида выражения, стоящего под знаком радикала, предпочтительно применять тот или иной способ.

       Как известно, квадратный трехчлен путем выделения полного квадрата может быть приведен к виду:

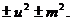
       Таким образом, интеграл приводится к одному из трех типов:

1)

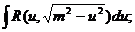
2)

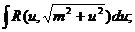
3)