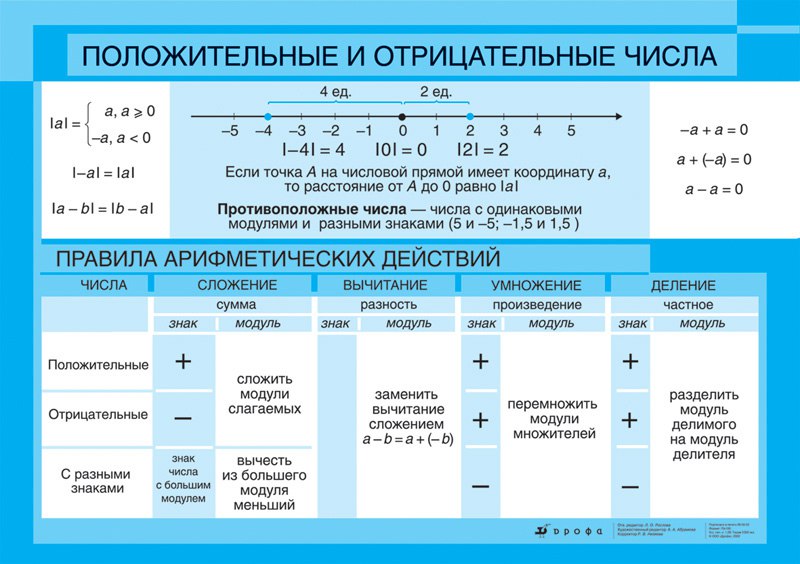
Сложений рациональных чисел обладает переместительным и сочетательным свойствами. Иными словами, если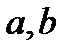 
и 
- любые рациональные числа, то
.
Прибавление нуля не изменяет числа, а сумма противоположных чисел равна нулю. Значит, для любого рационального числа имеем:
Умножение рациональных чисел тоже обладает переместительным и сочетательным свойствами. Другими словами, есл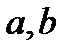и и - любые рациональные числа, то
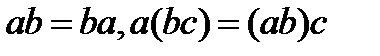
Умножение на 1 не изменяет рационального числа,а произведение числа на обратное ему число равно 1. Значит, для любого рационального числа а имеем:
, если 
.
Умножение числа на нуль дает в произведении нуль, т.е. для любого рационального числа 
имеем:
.
Произведение может быть равно нулю лишь в том случае, когда хотя бы один из множителей равен нулю.
Умножение рациональных чисел обладает и распределительным свойством относительно сложения. Другими словами, для любых рациональных чисел 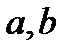и имеем:
.
Раскрытие скобок
Выражение 
. Эту операцию называют раскрытием скобок.
Если перед скобками стоит знак +,то можно опустить скобки и этот знак +, сохранив знаки слагаемых, стоящих в скобках. Если первое слагаемое в скобках записано без знака, то его надо записать со знаком +.
Чтобы записать сумму, противоположную сумме нескольких слагаемых, надо изменить знаки данных слагаемых. Значит,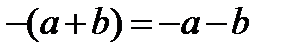 
.
Чтобы раскрыть скобки, перед которыми стоит знак –, надо опустить знак – и затем скобки, поменяв знаки всех слагаемых в скобках на противоположные, а потом раскрыть скобки.
Коэффициент
Если выражение является произведением числа и одной или нескольких букв, то это число называют числовым коэффициентом (или просто коэффициентом).
Коэффициент обычно пишут перед буквенными множителями. Коэффициентом такого выражения, как 
или 
, считают 1, так как 
Числовым коэффициентом выражения 
считают число -1.
Подобные слагаемые
Слагаемые, имеющие одинаковую буквенную часть, называют подобными слагаемыми.
Подобные слагаемые могут отличаться только коэффициентами.
Чтобы сложить (или говорят: привести) подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.
Решение уравнений
Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и то же число, не равное нулю.
Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую.изменив при этом его знак.
Уравнение, которое можно привести к виду 
, где 
с помощью приведения подобных слагаемых и переноса слагаемых, называют линейным уравнением с одним неизвестным.
Перпендикулярные прямые
Две прямые, образующие при пересечении прямые углы, называют перпендикулярными.
Отрезки, лежащие на перпендикулярных прямых, называют перпендикулярными отрезками.
Параллельные прямые
Две непересекающиеся прямые на плоскости называют параллельными.
Отрезки (лучи), лежащие на параллельных прямых называют параллельными отрезками (лучами).
Если две прямые в плоскости перпендикулярны третьей прямой, то они параллельны.
Через каждую точку плоскости, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной прямой.
Координатная плоскость
Если на плоскости провести две перпендикулярные координатные прямые – 
и 
, которые пересекаются в начале отсчета – точке 0, то эти прямые называют системой координат на плоскости, а точку 0 – началом координат. Плоскость, на которой выбрана система координат, называют координатной плоскостью.
Каждой точке на координатной плоскости соответствует пара чисел: ее абсцисса и ордината. Наоборот, каждой паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами.
Столбчатые диаграммы
Столбчатые диаграммы позволяют графически отобразить различия между данными.
Графики
График – чертеж, применяемый для наглядного изображения зависимости какой-либо величины (напр., пути) от другой (напр., времени), т. е. линия, дающая наглядное представление о характере изменения функции.
