Чтобы привести дроби к наименьшему общему знаменателю, надо: 1) найти наименьшее общее кратное знаменателей этих дробей, оно и будет их наименьшим общим знаменателем;
2) разделить наименьший общий знаменатель на знаменатели данных дробей, т.е. найти для каждой дроби дополнительный множитель; 3) умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
В более сложных случаях наименьший общий знаменатель и дополнительные множители находят с помощью разложения на простые множители.
Сравнение, сложение и вычитание дробей с разными знаменателями
Чтобы сравнить (сложить, вычесть) дроби с разными знаменателями, надо: 1) привести данные дроби к наименьшему общему знаменателю; 2) сравнить (сложить, вычесть) полученные дроби.
Сложение и вычитание смешанных чисел
Чтобы сложить смешанные числа, надо: 1) привести дробные части этих чисел к наименьшему общему знаменателю; 2) отдельно выполнить сложение целых частей и отдельно – дробных частей. Если при сложении дробных частей получилась неправильная дробь, выделить целую часть дроби и прибавить ее к полученной целой части.
При вычитании смешанных чисел пользуются свойствами вычитания суммы из числа и вычитания числа из суммы.
Если дробная часть уменьшаемого окажется меньше дробной части вычитаемого, то надо превратить в дробь с тем же знаменателем одну единицу целой части уменьшаемого.
Чтобы выполнить вычитание смешанных чисел, надо: 1) привести дробные части этих чисел к наименьшему общему знаменателю; если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить ее в неправильную дробь, уменьшив на единицу целую часть; 2) отдельно выполнить вычитание целых частей и отдельно дробных частей.
Умножение дробей
Чтобы умножить дробь на натуральное число, надо ее числитель умножить на это число. А знаменатель оставить без изменения.
Чтобы умножить дробь на дробь, надо: 1) найти произведение числителей и произведение знаменателей этих дробей; 2) первое произведение записать числителем, а второе – знаменателем.
Для того, чтобы выполнить умножение смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
Нахождение дроби от числа
Чтобы найти дробь от числа, нужно умножить число на эту дробь.
Применение распределительного свойства умножения
Распределительное свойство умножения относительно сложения и относительно вычитания позволяет упрощать вычисление.
Чтобы умножить смешанное число на натуральное число, надо: 1) умножить целую часть на натуральное число; 2) умножить дробную часть на это натуральное число; 3) сложить полученные результаты.
Взаимно обратные числа
Два числа, произведение которых равно 1, называются взаимно обратными.
Значит, взаимно обратными будут числа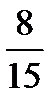 
и 
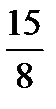, 7 и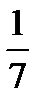 
. Числу 
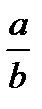, где 
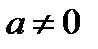и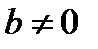 
, обратно число 
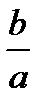. В самом деле, 
.
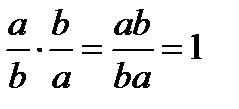Деление
Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю.
