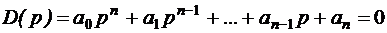
p = j w - придаем чисто мнимое значение.
Для того чтобы система была устойчивой, необходимо, чтобы суммарный угол поворота векторов р-р i составлял угол p n.
В характеристическом уравнении заменяем р на j w. Тогда получим функцию комплексного переменного:
,
которую можно так же, как амплитудно-фазовую характеристику, представить в виде суммы действительной и мнимой частей:
.
Действительная часть Re(w) содержит только четные степени переменного w:
,
а мнимая часть Im (w) – только нечетные:
Действительная часть характеристического уравнения является функцией четной, а мнимая часть – нечетной.
Поэтому достаточно ограничиться построением кривой, соответствующей характеристическому полиному для положительных частот. Тогда кривая, соответствующая отрицательным частотам является зеркальным отражением кривой для положительных частот относительно оси абсцисс.
Каждому фиксированному значению переменного w соответствует комплексное число, которое можно изобразить в виде вектора на комплексной плоскости. Если теперь изменять параметр w от 0 до ¥, то конец вектора D (j w) опишет некоторую линию, которая называется характеристической кривой или годографом Михайлова. По виду этой кривой можно судить об устойчивости системы.
Формулировка критерия Михайлова.
Автоматическая система управления, описываемая уравнением п -го порядка будет устойчивой, если при изменении частоты от 0 до ¥ характеристический вектор системы (годограф Михайлова) повернется против часовой стрелки на угол 
, не обращаясь при этом в нуль.
Это означает, что характеристическая кривая устойчивой системы должна при изменении w от 0 до ¥ пройти последовательно через n квадрантов. Кривая D (j w) для устойчивой системы всегда начинается в точке на действительной оси, удаленной от начала координат на величину 
(рис. 70).
Рисунок 70
На рисунке 70, а изображен вектор D (j w), называемый характеристической кривой или годографом Михайлова. Характеристические кривые, соответствующие устойчивым системам (рисунок 70, б), имеют плавную спиралеобразную форму и уходят в бесконечность в том квадранте, номер которого равен порядку уравнения. Если характеристическая кривая проходит п квадрантов не последовательно или проходит меньшее число квадрантов, то система неустойчива (рисунок 70, в).
В практических расчетах удобно применять следствие из критерия Михайлова.
Система устойчива, если действительная и мнимая части характеристической функции D (j w) обращаются в нуль поочередно (см. рисунок 70, г), т.е. если корни уравнений Re (w)=0 и Im (w)=0 перемежаются и Re (0) > 0 и Im ¢ (0) > 0.
Следствие из критерия Михайлова позволяет установить устойчивость системы невысокого порядка аналитически, без построения годографа.
11.3 Критерий устойчивости Найквиста.
Критерий Найквиста был сформулирован в 1932 г. американским физиком X. Найквистом. В отличие от критериев Гурвица, Рауса и Михайлова, которые основаны на анализе характеристического уравнения системы, критерий Найквиста позволяет судить об устойчивости замкнутой системы по амплитудно-фазовой характеристике разомкнутого контура системы.
В этом заключается существенное преимущество критерия, т.к. построение АФХ разомкнутого контура для большинства реальных систем оказывается проще, чем построение годографа Михайлова. Особенно упрощается это построение для одноконтурных систем, состоящих из типовых звеньев.
Имеется САУ (рис. 71):
здесь Dp (j w) – частотное характеристическое уравнение разомкнутой системы.
Рисунок 71
Найквист в своем критерии рассматривает вспомогательную функцию, определяемую по формуле
.
Примечание: Возьмем абстрактное комплексное число
.
Модуль этого числа будет равен произведению модулей каждого из множителей, а аргумент этого числа – сумме каждого из слагаемых.
.
Причем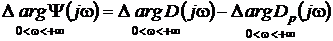 
.
Рассмотрим два случая.
1. Система в разомкнутом состоянии устойчива, это значит по Михайлову:
,
где п – порядок разомкнутой системы.
Частотное характеристическое уравнение замкнутой системы также имеет порядок п, т.к. порядок числителя разомкнутой системы всегда меньше или равен порядку знаменателя разомкнутой системы (
).
Если система в замкнутом состоянии тоже устойчива, то угол одинаковый
.
Рассмотрим изменения аргумента 
при изменении частоты от 0 до ¥:
.
Система в замкнутом состоянии будет устойчива, если изменение аргумента функции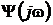 
при изменении частоты от 0 до ¥ составит ноль. Это возможно только в том случае, когда годограф не охватывает точку начала координат (рис. 72, а). Но если рассматривать годограф функции 
, то этому соответствует случай, когда не охватывается точка (-1; ј 0) (рис. 72, б).
Рисунок 72
Критерий Найквиста для первого случая: замкнутая система будет устойчивой, если годограф разомкнутой системы не пересекает отрезок (-¥;-1], т.е. не охватывает критическую точку (-1;0).
Употребленное в формулировке критерия Найквиста понятие охвата точки имеет некоторую неопределенность, из-за чего в случаях сложной формы кривой W (ј ω) могут возникнуть затруднения в суждении об устойчивости системы. Поэтому для суждения об устойчивости систем, имеющих АФЧХ сложной конфигурации, когда кривая АФЧХ пересекает действительную ось левее точки с координатами (-1; ј 0) несколько раз, можно также использовать правило переходов, сформулированное советским ученым Я. 3. Цыпкиным: АФЧХ не охватывает точку (-1; ј 0), если при возрастании w разность между числом положительных (сверху вниз) и отрицательных (снизу вверх) переходов АФЧХ через ось абсцисс слева от точки (-1; ј 0) равна нулю.
На рисунке 73, а изображен годограф системы, устойчивой в замкнутом состоянии, а на рисунке 73, б – системы, находящейся на границе устойчивости.
Рисунок 73
Система находится на границе устойчивости, если годограф, соответствующий амплитудно-фазовой характеристики разомкнутой системы хотя бы один раз пересечет точку [-1;0].
2. Разомкнутая система неустойчива.
Разомкнутая система неустойчива, это значит, что изменение аргумента представляется формулой:
,
где m – количество корней характеристического уравнения разомкнутой системы, находящихся в правой полуплоскости.
У замкнутой системы изменение аргумента при изменении частоты от 0 до ¥:
для устойчивой системы.
Изменение аргумента вспомогательной функции составит:
.
Тогда критерий Найквиста звучит так: если система неустойчива в разомкнутом состоянии и имеет m положительных корней характеристического уравнения, то система в замкнутом состоянии будет устойчива лишь в том случае, если годограф разомкнутой системы охватывает точку (-1; ј 0) в положительном направлении m раз, или, используя правило переходов: разность между количеством положительных переходов и количеством отрицательных переходов отрезка 
действительной оси будет равна 
.
Объединяя два случая, можно дать следующее определение критерия Найквиста.
Система в замкнутом состоянии будет устойчива, если разность между числами положительных и отрицательных переходов годографа АФЧХ разомкнутой системы на отрезке действительной оси будет равна , где т – количество правых корней характеристического уравнения разомкнутой системы.
Если АФЧХ начинается или заканчивается на отрезке (-∞; -1), то считают, что характеристика совершает полперехода.
Рекомендованная литература по лекции: [6].
Лекция 12 «Синтез линейных систем автоматического управления»
Все математические задачи, решаемые в теории автоматического управления, можно объединить в два больших класса – задачи анализа и задачи синтеза автоматических систем.
В задачах анализа полностью известна структура системы, заданы все (как правило) параметры системы, и требуется оценить какое-либо ее статистическое или динамическое свойство. К задачам анализа относятся расчет точности в установившихся режимах, определение устойчивости, оценка качества системы.
Задачи синтеза можно рассматривать как обратные задачам анализа: в них требуется определить структуру и параметры системы по заданным показателям качества. Простейшими задачами синтеза являются, например, задачи определения передаточного коэффициента разомкнутого контура по заданной ошибке или условию минимума интегральной оценки.
Под синтезом линейных САУ понимается выбор такой структурной схемы, ее параметров, характеристик, которые отвечают с одной стороны заданным показателям качества и простоты технической реализации и надежности с другой стороны.
Особенности синтеза.
1. САУ включает в себя объект управления и корректирующие устройства (это такие устройства, структура и параметры которых изменяются в соответствие с задачей синтеза).
2. Задание показателей качества определяется как верхняя граница допустимых показателей качества, т.о. заданные показатели качества определяют собой область принятия решений. Поэтому при синтезе выбирают критерий оптимизации, позволяющий определить однозначный выбор структуры и параметров САР.
3. Для современных САУ процедура синтеза определяет ориентировочную характеристику САУ, поэтому окончательный результат получается в результате анализа (настройки, моделирования) синтезированной САУ.
Этапы синтеза САУ.
1. Анализируется объект управления, определяются статические и динамические характеристики объекта.
2. Определяется критерий оптимизации, основанный на заданных показателях качества САУ.
3. Строится структурная схема САУ, выбираются технические средства ее реализации.
4. Синтез оптимальной динамической характеристики.
5. Аппроксимация оптимального динамического режима, т.е. выбор динамических характеристик (желаемых), отвечающих заданным показателям качества и простоте технической реализации корректирующих устройств.
6. Определение динамических характеристик корректирующих устройств, которые обеспечивают желаемые динамические характеристики всей системы.
7. Выбор схемы и способа технической реализации корректирующих устройств по заданной динамической характеристике корректирующего устройства.
8. Анализ синтезированных САУ.
Подробно методы и вопросы анализа и синтеза линейных САУ рассмотрены в [7].
Рекомендованная литература по лекции: [7].
Лекция 13 «Коррекция САУ»
13.1 Синтез по распределению полюсов и нулей передаточной функции.
13.2 Синтез по логарифмическим частотным характеристикам.
13.3 Оптимизация параметров САУ.
13.1 Синтез по распределению полюсов и нулей передаточной функции.
Методы синтеза по распределению полюсов и нулей передаточной функции, как правило, применяются тогда, когда число полюсов не превышает трсх-чстырсх, т. е. для уравнений невысоких порядков. Сложные системы этими методами синтезируются обычно тогда, когда переходные процессы в них определяются в основном небольшим числом доминирующих полюсов и нулей, ближе расположенных к мнимой оси, а влияние остальных, более удаленных, полюсов невелико, и при первоначальном синтезе их можно исключить. Чтобы оценить, можно ли синтезировать таким образом данную сложную систему, надо предварительно рассмотреть передаточную функцию замкнутой нескорректированной (но стабилизированной) системы и либо, численно вычислив или оценив корни се характеристического уравнения, установить, можно ли из них выделить доминирующие, либо рассмотреть, нельзя ли представить уравнение системы в виде
,
где μ - «малый параметр», а полиномы D 3, и М 3 имеют порядок не выше четвертого. В этом случае, когда это возможно, рассматривают вместо исходной замещающую систему, описываемую вырожденным уравнением
н передаточной функцией
.
При выделении доминирующих полюсов можно руководствоваться правилом, что если расстояние корня s 2 от мнимой оси в 6 раз и более превышает расстояние корня s 1 от мнимой оси, то корень s 1 является доминирующим, а корень s 2 можно в первом приближении отбросить. Точно так же можно считать компенсирующими друг друга и не принимать во внимание те диполи (близко расположенные друг к другу полюс и пуль), у которых модули отличаются не более чем на 5%, а фазы менее чем на 6°. После того, как найдено, что замкнутая нескорректированная система имеет небольшое число доминирующих нулей и полюсов, вводится предположение, что в результате коррекции число доминирующих корней сохранится, но их расположение на плоскости s с помощью корректирующих цепей будет приближено к желаемому. Эффективность сделанных допущений зависит от инженерной интуиции исследователя. Очевидно, что окончательный результат синтеза требует более точной проверки качества процессов в полученной системе.
Желаемое распределение полюсов и нулей устанавливают по заданным прямым показателям качества. Рассмотрим несколько основных простейших случаев определения желаемого распределения доминирующих корней исходя из условий, чтобы время регулирования Тр и перерегулирование σ при воздействии единичной ступенчатой функции не превышали заданных значений Tm и σ m.
Подробно методика синтеза по распределению полюсов и нулей передаточной функции изложена в [8, с. 230]
13.2 Синтез по логарифмическим частотным характеристикам.
Построение желаемой ЛАХ.
Построение желаемой ЛАХ разомкнутой системы обычно начинают с нанесения по заданным требованиям к качеству некоторых ее основных участков. К таким участкам относятся низкочастотная и высокочастотная асимптоты и среднечастотная часть.
Пусть замкнутая система воспроизведения для f (t) образована путем замыкания единичной отрицательной обратной связью разомкнутой системы с передаточной функцией W (s).
Наклон низкочастотной асимптоты к оси абсцисс зависит от порядка астатизма v, а ее расстояние от оси – от требуемых коэффициентов усиления или добротности разомкнутой цепи. По-рядок астатизма v принимается равным нулю, если при постоянном воздействии допускается статическая ошибка ε ст. При этом
,
и низкочастотная асимптота представляет собой прямую, параллельную оси абсцисс и удаленную от нее на расстояние, равное lg К логарифмических единиц (20 lg К, дБ).
Если статическая ошибка при постоянном воздействии недопустима, но при медленных изменениях воздействия (при низких частотах) допускается ошибка, пропорциональная скорости изменения воздействия, то принимается первый порядок астатиз (v = 1). При этом наклон низкочастотной асимптоты ЛАХ равен - 1 лог/дек (- 20 дБ/дек). Коэффициент добротности K д в астатической системе первого порядка определяется по заданной допустимой скоростной ошибке ε ск при заданной постоянной скорости изменения воздействия v = df / dt = const:
Для определения положения асимптоты достаточно задать одну из ее ординат. При частоте ω = 1 (ордината низкочастотной асимптоты в астатической системе первого порядка равна lg Кд, лог (20 lg К, дБ). Можно также задать точку пересечения асимптоты с осью абсцисс: ω н.с = K д.
Астатизмы второго и высших порядков требуются сравнительно редко. Если порядок астатизма равен v, то наклон низкочастотной асимптоты равен - v, лог/дек (- 20 v, дБ/дек), ее ордината при ω=1 равна lg Кд, лог (20 lg К, дБ), а точка пересечения с осью абсцисс 
. Чаще всего, исходя из условия наиболее легкого технического, осуществления коррекции, предполагают, что корректирующее звено не изменяет наклона высокочастотной асимптоты неизменяемой части системы, т. е. что высокочастотные асимптоты ЛАХ неизменяемой части и желаемой системы параллельны.
Среднечастотной частью называют отрезок ЛАХ в окрестности частоты, среза ω с, при которой коэффициент усиления в разомкнутой системе равен единице, т. е. при которой ЛАХ пересекает ось абсцисс.
В некоторых трудах предложено определять ω с так, чтобы она лежала в пределах
ω с 1 ≤ ω с ≤ ω с 2,
где нижняя граница ω с 1 находится по заданным времени регулирования Тр и перерегулированию σ из графиков. По σ определяют по одному из графиков Рмакс и Тр, выраженному в величинах π/ω с. Пусть оказалось, что Тр = k π/ω с.
Приравнивая эту величину заданному времени регулирования, найдем ω с 1= k π/ Тр.
Граница ω с 2 определяется из условия
.
Здесь Тмин означает время идеального процесса, который имеет место, если система из состояния x =0 сначала разгоняется с максимальным ускорением ω макс до половины заданного пути х 0/2, а затем тормозится с максимальным замедлением - ωмакс.
Приведенные оценки удобны тем, что позволяют установить (ω с весьма быстро и просто, но они являются лишь ориентировочными по ряду причин. Первая причина – фактическая вещественная частотная характеристика замкнутой системы неизвестна, а при составлении графиков принималось допущение, что она равна сумме двух трапеций. По этой же причине перед синтезом не известно, каким из двух изображенных графиков следует пользоваться. Вторая причина – в реальном процессе ускорения не будут постоянными, поэтому вычисление ω с 2 неточно.
В качестве среднечастотной части-желаемой ЛАХ далее принимается прямолинейный отрезок, проходящий через точку ω с с наклоном - 1 лог/дек (- 20 дБ/дек). Строгого обоснования для этой рекомендации нет, но большое число проведенных расчетов показывает, что при соблюдении этой рекомендации результаты синтеза получаются хорошими, а в противном случае качественная коррекция системы удается редко. В частности, ЛАХ системы, в которой реализуется точный оптимальный в указанном выше смысле режим, имеет в окрестности ωс именно такой наклон.
После нахождения асимптот и среднечастотной части в окрестности частоты среза нужно выполнить построение желаемой ЛАХ путем сопряжения трех найденных частей. Для этого прежде всего надо найти границы среднечастотной части. В трудах предложено устанавливать эти границы исходя из необходимого запаса устойчивости по амплитуде и фазе. В соответствии с рекомендациями по найденному из графиков Рмакс находим
Рмин = Рмакс – 1
и затем выбираем границы среднечастотной части так, чтобы в граничных точках и между ними желаемая ЛАХ не входила внутрь области, ограниченной на рис. 74 линиями Р = Рмакс и Р = Рмин.
Кривые, построенные на рис. 74, представляют собой линии постоянных значений ординат вещественных частотных характеристик Р=соnst-в координатах θ, 20 lg Н. Их свое•образная форма в виде симметричных восьмерок позволяет существенно упростить синтез. В самом деле, кривые Р = Рмакс и Р = Рмин симметричны относительно оси Lm Н =0. Их можно заменить описанным прямоугольником со сторонами ±θ m и ±Lm Нт. Внутри этого прямоугольника фазы не превышают значений θ m, а амплитуды - значений Нт. Если желаемая ЛАХ не входив в каком-то интервале частот внутрь этого прямоугольника, то она тем более не входит и внутрь кривых Р = Рмакс и Р = Рмин. Границы прямоугольника отображаются на ЛАХ в виде полосы ±20 lg H. Положение границ среднечастотной части ЛАХ следует выбирать так, чтобы в точках пересечения ее с границами упомянутой полосы и между ними запас по фазе был не меньше заданного.
Рисунок 74
После определения границ среднечастотной части она далее сопрягается с асимптотами так, чтобы обеспечивалась наиболее простая форма корректирующего звена. Техническая реализация звена тем проще, чем меньше изломов имеет его ЛАХ. Из последующего легко видеть, что наименьшее число изломов в характеристике звена будет иметь место в том случае, когда изломы желаемой ЛАХ происходят при тех же частотах, что и изломы ЛАХ неизменяемой части. Поэтому переход от границ среднечастотной части к асимптотам выполняется с помощью прямолинейных отрезков (так, чтобы сопрягающие частоты желаемой ЛАХ и ЛАХ неизменяемой части совпадали), по возможности наклоненных друг к другу под теми же углами, под какими встречаются соответствующие отрезки ЛАХ неизменяемой части.
Построения желаемой фазовой ЛЧХ при таком способе не требуется - вместо нее выполняется проверка соблюдения запасов устойчивости, описанная выше.
Возможны и другие варианты построения желаемой ЛАХ, например, по нескольким заданным коэффициентам ошибок с 0, с 1 ... и запасу устойчивости по фазе γ.
Весьма удобна для синтеза желаемых ЛАХ серия графиков Г. Честната и Р. Майера. Для систем приемлемого качества из графиков эмпирически установлены грубо приближенные соотношения: при 1,З≤М≤1,5
tp ≈ π / ω c; 1 + σ ≈ 0,85 М;ω t ≈ ω m ≈ 0,75 ω c.
13.3 Оптимизация параметров САУ.
Детерминированная задача синтеза оптимального управления исследована наиболее подробно. Необходимые и достаточные условия существования оптимальной временной программы управления при ограничениях были установлены в рамках классического вариационного исчисления. Необходимые условия существования оптимальной временной программы управления при ограничениях общего вида были сформулированы Л. С. Понтрягиным в виде принципа максимума и использованы для разработки математических методов оптимального управления. Сведение проблемы оптимизации программы управления к проблеме моментов позволило Н. Н. Красовскому создать наиболее общую теорию оптимального программного управления, дать новую постановку задачи оптимального управления при преследовании и предложить способы перехода от временной программы управления к параметрической.
Теория оптимального управления для решения практических задач долгое время не находила применения, так как непосредственное использование необходимых и достаточных условий оптимальности управления для построения алгоритма оптимизации управления не всегда могло дать приемлемые с точки зрения вычислительной процедуры результаты, особенно при решении задач оптимизации управления в системах высокого порядка. Поэтому некоторое время были широко распространены численные методы, основанные на идеях динамического программирования. Но противоречие между требуемой точностью п размерностью задачи, свойственное этим методам, заставило обратиться к поискам приближенных методов, свободных от этого недостатка. Весьма эффективный подход к решению задач оптимизации программы управления, основанный на понятии элементарной операции, был разработан Н. Н. Моисеевым. Из численных методов, основанных на последовательном уточнении управления, приобрел широкую известность метод градиента, предложенный Г. Д. Келли. К недостаткам этого метода относится уменьшение скорости сходимости по мере приближения к экстремуму.
Результаты сравнения различных методов оптимизации программы управления и анализа общей тенденции развития численных методов оптимизации управления позволяют считать, что наиболее широкий класс задач может быть решен методами, основанными на сведении задач оптимизации управления при наличии ограничений к задачам нелинейного программирования.
Основной недостаток этих методов тот же, что и метода динамического программирования, устраняется при использовании процедуры последовательной оптимизации. Одной из характерных черт метода последовательной оптимизации является возможность его использования как в детерминированных задачах синтеза оптимальных программ управления (как временных, так и параметрических), так и в стохастических задачах синтеза оптимальных законов управления, а также для синтеза оптимального управления в игровых задачах. Противоречие между требуемой точностью и размерностью задачи устраняется в методе последовательной оптимизации путем построения эффективных итеративных процессов, позволяющих без снижения точности получаемого решения оперировать на каждом этапе приближения с приемлемым числом переменных.
Стохастическая задача синтеза оптимального нелинейного закона управления имеет дополнительные сложности по сравнению с детерминированными задачами. Общая теория оптимального стохастического управления, развитая в работах В. С. Пугачева и А. А. Красовского, показала, что даже в сравнительно простых случаях линейных систем условия оптимальности управления дают уравнения, которые в общем случае могут быть решены лишь приближенно. Это обстоятельство способствовало развитию методов оптимизации управления, в которых стохастическая задача синтеза оптимального управления заменяется детерминированной, а в качестве критерия оптимальности выбирается характеристика таких свойств системы, которые позволяют предполагать, что получаемое в результате синтеза управление окажется удовлетворительным во всех возможных реализациях управляемого процесса. В качестве подобных характеристик обычно рассматриваются распространенные показатели качества управления, например устойчивость, быстродействие и т. п. Если учесть типичную для большинства практических задач недостаточную достоверность информации о случайных воздействиях, то такой подход следует признать вполне закономерным, так как он позволяет значительно сузить класс допустимых управлений и в известном смысле гарантировать близость получаемого управления к оптимальному управлению в стохастической задаче, Дисперсионные характеристики управляемого процесса требуют специальной оценки. Такой подход к решению задач оптимизации управления представлен в последующих главах. Принятые в этих главах способы сужения области допустимых управлений позволили построить достаточно эффективные методы отыскания управлений, оптимальных по различным критериям или близких к оптимальным.
Другое направление, развиваемое в работах Н. Н. Красовского, предусматривает замену стохастической задачи оптимизации управления задачей с неопределенностью или с антагонистическим управлением и позволяет использовать для построения оптимального управления аппарат теории игр. Такая постановка позволяет найти наилучшее управление для наихудшего случая. Для численного решения игровых задач такого типа могут быть использованы методы, хорошо зарекомендовавшие себя при решении детерминированных задач оптимизации управления, в частности метод последовательной оптимизации.
Более подробно вопросы последовательной оптимизации, в том числе нелинейного закона управления, приведены в [9, с. 22].
Рекомендованная литература по лекции: [8, 9].
Содержательный раздел 5 «Нелинейные САУ. Импульсные САУ»
Лекция 14 «Основы теории нелинейных систем автоматического управления»
14.1 Понятие о нелинейных системах.
14.2 Особенности нелинейных систем. Типовые нелинейные элементы и их характеристики.
14.1 Понятие о нелинейных системах.
Динамическая система считается нелинейной, если она содержит хотя бы один нелинейный элемент или нелинейное звено.
В системах автоматического управления различают два вида нелинейностей: статические и динамические.
Статические нелинейности – это нелинейности статических характеристик. Выходная переменная статических нелинейных звеньев в каждый момент времени зависит только от значений входной переменной в тот же момент времени и не зависит от того, как эта входная переменная изменялась до рассматриваемого момента времени. Таким образом, вход и выход нелинейного звена связаны между собой нелинейной статической характеристикой 
.
Динамические нелинейности – это нелинейности дифференциальных уравнений, описывающих звено, например, 
.
В наиболее распространенных случаях нелинейные свойства системы в основном определяются наличием в системе статических нелинейностей. Поэтому рассматриваемый класс нелинейных систем ограничим нелинейностями только статического вида.
Различают статические нелинейности существенные и слабые. Нелинейность считается слабой, если она может быть заменена линейным элементом без изменения ринципиальных особенностей системы, причем процессы в такой линеаризованной системе качественно не должны отличаться от процессов в реальной системе.
Нелинейность является существенной, если подобная замена невозможна.
Главные особенности этих систем вытекают из их неподчинения принципу суперпозиции:
1. Колебания переходного процесса в нелинейных системах могут отличаться от входного гармонического сигнала, как по форме, так и по частоте, например, если 
.
2. В нелинейных системах аппарат частотных характеристик не подходит. Здесь частотные характеристики существенно зависят от амплитуды входного сигнала.
3. В нелинейных системах условия устойчивости зависят от величины внешнего воздействия: система устойчива при одних значениях воздействий и неустойчива при других его значениях. Для некоторых нелинейных систем, имеющих зону нечувствительности, наблюдается континиум состояний равновесия. Таким образом, в нелинейных системах говорят только об устойчивости конкретного состояния равновесия – устойчиво оно или нет.
4. В нелинейных системах могут существовать собственные особые движения, получившие название автоколебаний. Автоколебания – это устойчивые собственные колебания, возникающие из-за нелинейных свойств системы при особых условиях.
14.2 Особенности нелинейных систем. Типовые нелинейные элементы и их характеристики.
К нелинейным относятся системы, в которых связь между выходным и входным сигналами одного или нескольких основных элементов задастся нелинейными уравнениями. Любая реальная САУ всегда содержит нелинейности вследствие наличия люфтов, трения, ограниченной мощности исполнительных элементов и других факторов. Если влияние нелинейностей на систему несущественно, то ее можно линеаризовать. Это позволяет свести рассмотрение динамических свойств САУ к решению линейной задачи. Однако на практике часто приходится встречаться с САУ, которые имеют существенные нелинейные характеристики, влияющие на динамические свойства системы.
Нелинейности, встречающиеся в САУ, либо являются неотъемлемыми физическими свойствами элементов (например, сухое трение, люфт, прилипание, насыщение и т.д.), либо преднамеренно вводятся в систему для получения требуемых показателей качества САУ (например, релейные усилители, нелинейные корректирующие устройства и т. д.).
Нелинейные системы могут обладать качественными особенностями, которые несвойственны линейным системам. К таким особенностям относятся, например, возникновение периодических колебаний (называемых автоколебаниями), возможность нескольких равновесных состояний, только часть которых устойчива, переход системы из одного установившегося движения в другое иод действием внешних сил и т д.
Обычно в любой нелинейной САУ можно выделить группу линейных элементов (ЛЭ) и один или несколько нелинейных (НЭ). При одном нелинейном элементе структурная схема САУ может быть представлена как одноконтурная, состоящая из последовательно включенных линейных и нелинейного элементов (рис. 75). При других видах включения линейных и нелинейных частей САУ ее также можно привести к схеме, показанной на рис. 75, с помощью структурных преобразований. При составлении структурной схемы нелинейной САУ вместо нелинейного элемента обычно указывают его нелинейную статическую характеристику или, если это возможно, записывают аналитическое выражение нелинейной функции элемента. Нелинейные статические характеристики могут быть разбиты на две группы: однозначные и неоднозначные.
Рисунок 75
Нелинейные элементы с однозначной нелинейной характеристикой имеют однозначную зависимость между входным и выходным сигналами как при увеличении, так и при уменьшении входного сигнала. Элементы с неоднозначной нелинейной характеристикой имеют разные зависимости между входным и выходным сигналами, которые определяются знаком изменения входного сигнала. Указанные группы нелинейностей можно классифицировать и по другим признакам. В табл. 4 приводятся некоторые типовые нелинейные характеристики и аналитические зависимости между входным сигналом х и выходным у. Нелинейности типа насыщения, зоны нечувствительности и релейного переключения имеют однозначные и симметричные характеристики, а нелинейности типа люфта и насыщения с петлей гистерезиса - неоднозначные и, как правило, несимметричные.
Соединение нелинейных звеньев и зависимости, описывающие их поведение приведены на рис. 76.
а б в
Рисунок 76 – Последовательное (а), параллельное (б) и смешанное (в) соединения нелинейных звеньев
Следует отметить, что к нелинейным САУ в отличие от линейных неприменим метод суперпозиции, который дает возможность определить движение линейной САУ под воздействием возмущения как сумму частных составляющих от отдельных компонентов возмущения. Так, например, определенные сведения о переходном процессе в нелинейной САУ при подаче единичного входного воздействия не позволяют оценить реакции системы на скачкообразное воздействие большей или меньшей величины. Невозможно также предвидеть, какова будет реакция системы на линейно возрастающий сигнал, даже если известна реакция па скачкообразное воздействие. Таким образом, нельзя использовать известную реакцию САУ на сигнал одного вида для определения реакции на сигнал другого вида. Причем реакция системы на определенный сигнал зависит также и от вида нелинейности, присущей данной системе. На рис. 77 показано изменение гармонического сигнала в зависимости от вида нелинейности. Обычно при гармоническом входном возмущении на выходе нелинейного элемента появляются сложного вида периодические колебания. Кроме основной гармоники они содержат также высшие гармоники (которые ка рис. 77 не приводятся). Следовательно, анализ и синтез нелинейных САУ оказывается значительно сложнее, чем линейных.
Рисунок 77
Рекомендованная литература по лекции: [9, 10].
Лекция 15 «Устойчивость нелинейных систем»
15.1 Понятие устойчивости.
15.2 Критерий абсолютной устойчивости состояния равновесия. Общий критерий устойчивости процессов.
15.1 Понятие устойчивости.
При анализе нелинейных САУ прежде всего определяются возможные состояния равновесия системы и исследуется их устойчивость, определяются периодические движения и исследуется их устойчивость, изучаются процессы перехода от одного к другому установившемуся состоянию при разных начальных условиях. Началом анализа нелинейных САУ обычно является определение устойчивости системы и наличия автоколебаний.
Возможные состояния равновесия. Из-за наличия нелинейных характеристик выходной сигнал нелинейной САУ не будет пропорционален входному, поэтому форма реакции системы на скачкообразное воздействие будет зависеть от величины этого воздействия. Для некоторых нелинейных САУ применение входного воздействия может превратить устойчивый переходный процесс в неустойчивый, и наоборот. (В то время как устойчивость линейной САУ зависит только от ее параметров и не зависит от внешних воздействий).
В нелинейной САУ статические и динамические процессы значительно разнообразнее, чем в линейной. Характер переходного процесса в нелинейной системе часто зависит от величины начального отклонения, вызванного возмущением. В связи с этим для нелинейных СЛУ употребляются понятия устойчивости в малом, большом и в целом. Система устойчива в малом, если она устойчива при бесконечно малых отклонениях от исходного режима. Система устойчива в большом, если она устойчива при конечных отклонениях, возможных в данной системе по условиям ее работы. Система устойчива в целом, если она устойчива при неограниченных отклонениях.
15.2 Критерий абсолютной устойчивости состояния равновесия. Общий критерий устойчивости процессов.
Наиболее общие результаты по исследованию устойчивости любых нелинейных САУ могут быть получены с помощью метода А. М. Ляпунова. Для этого необходимо подобрать некоторую знакоопределенную функцию V (х 1, х 2, … хп) и вычислить производную по времени от этой функции
с учетом уравнения движения системы dxi / dt = fi (x 1, x 2, …, xn) (i = 1, 2, …, n), где xi - координаты системы; fi - известные функции, заданные в пространстве этих координат.
Знакоопределенной функцией называется такая функция, которая во всех точках некоторой области вокруг начала координат сохраняет один знак и нигде, кроме начала координат, не обращается в нуль. Если же функция сохраняет знак во всех точках этой области, но обращается в нуль и в других точках области, то она называется знакопостоянной функцией.
Если при V >0 имеет место W <0, то САУ называется асимготически устойчивой. Если при V >0 имеет место W =0, то САУ называется устойчивой. Сформулированные условия устойчивости составляют основу метода Ляпунова, который заключается в отыскании для исследуемой нелинейной САУ функции V, удовлетворяющей выдвинутым требованиям и называемой функцией Ляпунова.
Трудность использования этого метода в том, что отсутствуют общие правила отыскания функции Ляпунова. Данный метод позволяет получить достаточные условия устойчивости, которые не всегда будут необходимыми. Другими словами, при выполнении условий устойчивости система будет устойчивой, но эти условия могут не охватывать всей области ее устойчивости. От удачного подбора функции Ляпунова будет зависеть степень близости полученных условий устойчивости к необходимым и достаточным.
Если при исследовании устойчивости нелинейной САУ методом Ляпунова получены условия устойчивости, не зависящие от формы нелинейной характеристики, которая ограничена в некоторой области, то они называются условиями абсолютной устойчивости. В связи с этим принято считать, что абсолютно устойчивая нелинейная САУ устойчива при любых начальных отклонениях для любой формы нелинейной характеристики, принадлежащей к некоторому определенному классу
Рекомендованная литература по лекции: [9, 10].
Лекция 16 «Процессы в нелинейных системах»
16.1 Понятия состояния равновесия и автоколебаний.
16.2 Возможные режимы нелинейных систем. Критерий Попова.
16.3 Фазовые траектории.
16.1 Понятия состояния равновесия и автоколебаний.
Для нелинейных систем характерен режим незатухающих колебаний, которые возникают в них при отсутствии периодических внешних воздействий вследствие внутренних свойств системы. Эти колебания могут быть как устойчивыми, так и неустойчивыми. Устойчивые колебания нелинейных САУ называются автоколебаниями. Если колебания в нелинейной САУ устанавливаются в результате периодических внешних воздействий, то они называются вынужденными. Следует заметить, что при затухающих колебаниях переходного процесса происходит изменение периода колебаний.
Нелинейные дифференциальные уравнения, к которым приводит исследование САУ, часто имеют довольно высокий порядок. В настоящее время большинство групп нелинейных уравнений не может быть решено в общем виде. В конкретном случае иногда можно исследовать нелинейную систему точными аналитическими методами. Для этого необходимо, чтобы нелинейные характеристики были выражены посредством аналитических зависимостей. Но так как в большинстве случаев это невозможно, то при исследовании нелинейных САУ большую роль приобретают различные приближенные методы.
Использование приближеиных методов, как правило, не дает достаточно полного представления о всех динамических свойствах САУ. Поэтому применение нескольких методов в каждом конкретном случае часто дает более полную картину анализа. Тем не менее, использование каждого из приближенных методов позволяет исследователю ответить на ряд отдельных существенных вопросов, например об устойчивости, наличии в системе автоколебаний, характере каких-либо режимов и т. д. В настоящее время разработано большое количество методов исследований нелинейных САУ. Многие из них пригодны только для ограниченного круга задач и лишь некоторые имеют достаточно общее применение в области исследования нелинейных САУ.
Исследование нелинейных САУ можно также производить методами математического моделирования, которые могут быть реализованы с помощью аналоговых или вычислительных элементов. Эффективность их в том, что динамику сложной и дорогостоящей реальной САУ можно исследовать с помощью сравнительно простой электронной аппаратуры. Применение электронных моделей предпочтительнее при исследовании систем, описываемых сложными нелинейными дифференциальными уравнениями, математическое решение которых оказывается невозможным. Однако использование электронных моделей для исследования САУ не исключает необходимости аналитических методов расчета, как точных, так и приближенных, позволяющих получать обобщающие результаты.
16.2 Возможные режимы нелинейных систем. Критерий Попова.
При исследовании устойчивости нелинейных систем исследуют отдельные виды движения – состояние равновесия и автоколебания.
Одним из точных методов (критериев) анализа устойчивости нелинейных САР, не утративших свою актуальность и в настоящее время, является критерий абсолютной устойчивости В.М. Попова.
В этом критерии нелинейная САР условно разделена на чисто линейную часть, обычно расположенную в прямой цепи, и чисто нелинейную часть, обычно расположенную в цепи обратной связи (рис. 78).
Рисунок 78
В «классическом» варианте доказательства данного критерия принят ряд допущений:
1. Нелинейная часть – безинерционна.
2. Статическая характеристика нелинейной части является однозначной (без гистерезиса) и вписывается в Гурвицев угол К (0 < K < 
).
3. Линейная часть должна быть устойчивой, или в особых случаях иметь не более 2-х полюсов, расположенных на мнимой оси, при всех остальных полюсах передаточной функции, расположенных в левой полуплоскости.
4. В особых случаях должна иметь место предельная устойчивость.
В.М. Попов ввел понятие видоизмененной АФЧХ, обозначаемой обычно 
и определяемой соотношениями: 
, где 
; 
; 
; 
, 
– действительная и мнимая части АФЧХ линейной части, соответственно.
Существуют аналитическая и геометрическая формулировки абсолютной устойчивости по В.М. Попову. Более наглядной является геометрическая формулировка.
Для того, чтобы имела место абсолютная устойчивость в угле [0; К ] в основном и в угле [ eps; К ] (где eps – бесконечно малое положительное число) в особых случаях, достаточно, чтобы в плоскости можно было выбрать прямую, проходящую через точку действительной оси с абсциссой – 1/ K так, чтобы годограф весь лежал строго справа от этой прямой и чтобы, кроме того, в особых случаях имела место предельная устойчивость.
На рис. 79 представлена графическая иллюстрация критерия Попова при анализе устойчивости нелинейной САР, где пунктирной линией представлен традиционный годограф Найквиста (годограф АФЧХ) для линейной части САР (W_лин), сплошной линией представлен видоизмененный годограф Попова, а точка на оси абсцисс с координатой - 1/ K (K – Гурвицев угол) расположена левее точки пересечения годографа Попова с осью абсцисс.
Рисунок 79 – Годографы Найквста и Попова
Очевидно, что через точку -1/ К можно провести бесчисленное множество прямых.
На рис. 79 одна из множества прямых проведена так, что видоизмененный годограф Попова лежит строго справа от этой прямой.
Резюме: нелинейная САР абсолютно устойчива.
Следует отметить, что условие устойчивости, вытекающее из критерия устойчивости Попова, являются достаточным, но не необходимым.
Иными словами: если выполняются условия критерия Попова, то система гарантировано устойчива. Но, если условие Попова не выполняется, то система может быть как устойчива, так и неустойчива.
Подробно метод В. М. Попова изложен в [10, с. 83].
16.3 Фазовые траектории.
Фазовый метод основан на понятии о фазовом пространстве. В принципе фазовым методом можно исследовать системы, которые описываются дифференциальными уравнениями любого порядка. Суть метода сводится к следующему. Если САУ описывается дифференциальным уравнением п -го порядка, то ее состояние может быть задано п числами, которые можно рассматривать как задание некоторой точки в п -мерном пространстве. При этом каждой точке п -мерного пространства будет соответствовать одно определенное состояние (определенная фаза) системы. Поэтому такое многомерное пространство называется фазовым пространством. Ввиду затруднений, возникающих при рассмотрении п -мерного пространства при п >3, применение фазового метода ограничено системами не выше третьего порядка.
Для САУ, которые описываются дифференциальиыми уравнениями второго порядка, фазовое пространство является двумерным, т. е. превращается в фазовую плоскость. На фазовой плоскости (рис. 80) но оси абсцисс откладывается значение исследуемой переменной х (обычно отклонение управляемого сигнала от заданного значения), а по оси ординат – скорость изменения этой переменной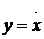 
. Состояние САУ второго порядка в каждый момент времени характеризуется значениями координат х и у, что соответствует определенной изображающей точке на фазовой плоскости, например точке М на рис. 80.При изменении состояния системы изображающая точка на фазовой плоскости перемещается по кривой, которая называется фазовой траекторией. Направление движения изображающей точки обозначают на траектории стрелками. Направление движении изображающей точки в верхней полуплоскости всегда может быть только слева направо, т. е. в сторону увеличения х, а в нижней полуплоскости – справа налево. Фазовая траектория пересекает ось абсцисс всегда под прямым углом. Это следует из того, что в точке пересечения производная у = dx / dt = 0, и поэтому координата х должна быть экстремальной.
Рисунок 80
Фазовые траектории устойчивой САУ должны стремиться к началу координат при неограниченном возрастании времени. А фазовые траектории неустойчивой САУ должны неограниченно удаляться от начала координат фазовой плоскости. Замкнутым фазовым траекториям соответствуют периодические процессы.
Для получения уравнения фазовых траекторий исходно уравнение системы преобразуют таким образом, чтобы можно было исключить время. Если САУ описывается дифференциальным уравнением второго порядка, то его следует свести к двум уравнениям первого порядка:
*
где f 1 и f 2 – в общем случае нелинейные функции координат х и у.
Дифференциальное уравнение фазовых траекторий в плоскости ху получается при исключении времени из уравнений (*). Для этого второе уравнение делят на первое:
.
Решением этого уравнения будет некоторая функция у = F (x), графическое изображение которой дает фазовую траекторию на плоскости ху.
Рассмотрим типичные виды фазовых траекторий, одиовременно связывая их построение с анализом переходного процесса.
Затухающий колебательный процесс. Если начальные условия переходного процесса ненулевые (рис. 81, а), т.е. х = х 0, х = х 0 = у, то на фазовой плоскости (см. рис. 81, б) начальная изображающая точка М 0 будет иметь координаты х 0 и у 0,. В начале переходного процесса значение координаты х увеличивается до точки 1, а координаты у = х уменьшается. Изображающая точка на фазовой плоскости будет перемещаться по траектории от точки М 0 до точки 1, в которой имеет место максимум величины х и у = х = 0. На участке 1-2 процесс в системе идет с уменьшением координаты х, т. е. с отрицательной производной у=х< 0. Аналогичным образом можно построить остальные точки (3, 4, 5 и т. д.) фазовой траектории. В результате на фазовой плоскости получим фазовый портрет затухающего колебательного процесса, который изобразится в виде спирали, свертывающейся к началу координат. Начало координат фазовой плоскости соответствует устойчивому установившемуся режиму в системе, где х = 0и у = х = 0. В данном случае начало координат называется устойчивым фокусом (рис. 81, б).
Расходящийся колебательный процесс. Рассуждая аналогичным образом, можно построить фазовый портрет для расходящихся колебаний переходного процесса (рис. 82, а). Фазовая траектория будет иметь вид спирали, удаляющейся от начала координат (рис.82, б). Если такой фазовый портрет возникает при сколь угодно малом начальном отклонении, то система будет неустойчива в равновесном состоянии (х = 0 и у = 0). Начало координат фазовой плоскости в этом случае называется неустойчивым фокусом.
Периодический колебательный процесс. Если колебательный процесс в системе периодический (рис. 83, а), то он на фазовой плоскости изобразится в виде замкнутой кривой, которая называется циклом (рис. 83, б). Для синусоидальных колебаний фазовая траектория имеет вид эллипса, а для несинусоидальных колебаний – вид произвольной замкнутой кривой. Начало координат фазовой плоскости называется центром.
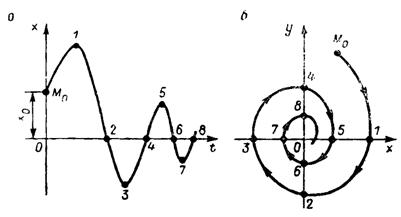
Рисунок 81
Рисунок 82
Рисунок 83
Апериодический затухающий процесс, разновидности которого изображены на рис. 84, а, на фазовой плоскости будет изображаться в виде кривой, вливающейся в начало координат (рис. 84, б). При этом изображающая точка, двигаясь по фазовой траектории, асимптотически приближается к началу координат при t →∞. Начало координат фазовой плоскости на-ывается устойчивым узлом.
Апериодический расходящийся процесс, варианты которого представлены на рис. 85, а, на фазовой плоскости изобразится в виде кривой, удаляющейся от начала координат (рис. 85, б). В случае, когда процесс расходится при сколь угодно малом начальном отклонении, начало координат фазовой плоскости называется неустойчивым узлом.
Устойчивые автоколебания. Если на фазовой плоскости существует замкнутая фазовая траектория (рис. 86), к которой в пределе стремятся все фазовые траектории плоскости, то такая замкнутая кривая называется устойчивым предельным циклом. Все фазовые траектории, находящиеся внутри предельного цикла, соответствуют расходящемуся процессу и в пределе сливаются с замкнутой фазовой траекторией (предельным циклом). Фазовые траектории, находящиеся снаружи предельного цикла, будут соответствовать сходящемуся процессу и в пределе также сольются с замкнутой фазовой траекторией.
Неустойчивые автоколебания. Если на фазовой плоскости существует замкнутая фазовая траектория (рис. 87), от которой внутрь и наружу расходятся фазовые траектории, то такая замкнутая кривая называется неустойчивым предельным циклом. Фазовые траектории, находящиеся внутри этого предельного цикла, соответствуют сходящемуся процессу, а находящиеся снаружи – расходящемуся процессу. Следовательно, если начальная точка процесса М 0(х 0, у 0) находится внутри предельного цикла, то система устойчива. Если же эта точка аходится вне его, то система будет неустойчива. Такая система называется устойчивой в малом и неустойчивой в большом.
Таким образом, устойчивость нелинейной САУ может зависеть также и от начальных условий.
Периодический режим, который соответствует неустойчивому предельному циклу, в реальных САУ не может долго существовать, поскольку любое случайное воздействие вызовет изменение фазовой траектории.
Рисунок 84
Рисунок 85
Рисунок 86 Рисунок 87
Определим фазовый портрет для точки, которая совершает гармонические колебания по закону х = А sin(ω t) (см. рис. 83, а). Для построения фазового портрета найдем скорость изменения координаты х. В рассматриваемом примере
y = dx/dt = ω А cos(ω t).
Исключив время t из уравнений для х и у, получим уравнение фазовых траекторий
.
Из последнего выражения следует, что периодические колебания на фазовой плоскости имеют замкнутые траектории – эллипсы (см. рис. 83, б). При этом разным амплитудам колебаний на фазовой плоскости соответствует семейство эллипсов.
Построим фазовый портрет для точки, совершающей затухающие колебания:
.
В данном случае скорость изменения координаты х определяется уравнением
Исключив время t из уравнений для х и у, получим уравнение для фазовых траектории, которые определяются свертывающимися спиралями:
.
График затухающих колебаний точки и ее фазовый портрет для рассматриваемого примера изображены па рис. 81.
Рекомендованная литература по лекции: [9, 10].
Лекция 17 «Нелинейные импульсные системы»
17.1 Виды дискретных систем.
17.2 Основные характеристики импульсных систем.
17.3 Стохастические процессы. Реакция нелинейной системы на случайное воздействие.
17.4 Дисперсия ошибки.
17.1 Виды дискретных систем.
Сигналы, действующие в САУ, бывают непрерывными и дискретными. Соответственно все САУ делятся на системы непрерывного действия и системы дискретного действия.
В системах непрерывного действия существуют только аналоговые сигналы, являющиеся непрерывными функциями времени (см.рис. 88, a). Все звенья этих САУ – звенья непрерывного действия, т.е. их входные и выходные величины представляют собой непрерывные сигналы.
САУ дискретного действия называются системы, в которых хотя бы одна величина представляет собой дискретный сигнал. Дискретный сигнал изменяется во времени дискретно, скачками. Существуют дискретные САУ, в которых имеются только дискретные сигналы. Такие системы состоят полностью из звеньев дискретного действия, входные и выходные величины которых являются дискретными. Однако, в большинстве дискретных систем имеются как дискретные так и непрерывные сигналы. В состав таких систем, наряду с дискретными и непрерывными звеньями, входят звенья, преобразующие непрерывные сигналы в дискретные и наоборот.
Преобразование непрерывного сигнала в дискретный называется квантованием (дроблением) сигнала. Существует два основных вида квантования: по уровню и по времени.
