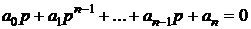Автоматическая система, описываемая характеристическим уравнением

,

устойчива, если при a ₀>0 положительны все определители ∆₁, ∆₂,...∆ _п вида

.

Если хотя бы один из определителей, называемых определителями Гурвица, отрицателен, то система неустойчива. Если главный определитель ∆ _п =0, а все остальные определители положительны, то система находится на границе устойчивости.

Рассмотрим частные случаи критерия Гурвица для n =1;2;3;4. Раскрывая определители, фигурирующие в общей формулировке критерия, можно получить следующие условия.

1. Для уравнения первого порядка (n =1)

условие устойчивости: а ₀>0 и ∆₁= а ₁>0, т.е. для устойчивости системы необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были больше нуля.

2. Для уравнения второго порядка (n =2)

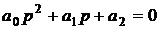
условие устойчивости:

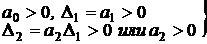
Т.о., и для системы второго порядка необходимое условие устойчивости (положительность коэффициентов) является одновременно и достаточным.

3. Для уравнения третьего порядка (n =3) 

условие устойчивости:

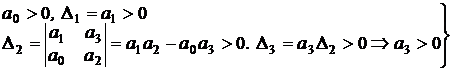
При n =3 для устойчивости системы необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были больше нуля и произведение средних коэффициентов уравнения (а ₁, а ₂) было больше произведения крайних (а ₀, а ₃).

4. Для уравнения четвертого порядка (n =4)

кроме положительности всех коэффициентов требуется выполнение условия

.

При n =4 система будет устойчива при всех коэффициентах больших нуля и при .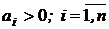

Т.о., для устойчивости систем не выше четвертого порядка необходимо и достаточно, чтобы все коэффициенты характеристического уравнения и определитель ∆ _{п -1} были положительными.

Критерий Рауса.

САУ будет устойчивой, если будут положительны все элементы первого столбца таблицы Рауса (включая а ₀ и ш₁).

,

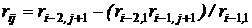где i – номер строки, j – номер столбца.

Если не все коэффициенты столбца положительны, то система неустойчива. При этом число перемен знака среди этих коэффициентов соответствует числу правых корней характеристического уравнения.

Таблица:

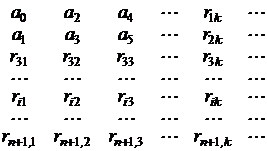
Пример.

Характеристическое уравнение:

 

10.3. Положения А.М. Ляпунова.

Когда известно общее решение дифференциальных уравнений движения, можно непосредственно определить значения переменных y _i (t) в возмущенном движении, составить вариации x _i = y _i (t) - y _i * (t) и, исследуя их, решить вопрос об устойчивости невозмущенного движения y _i * (t). Однако, как правило, исследование устойчивости движения производят не путем анализа общего решения, а методами, основанными на качественном анализе дифференциальных уравнений возмущенного движения, которым удовлетворяют отклонения (вариации) x _i.

Подробный вывод нижеприведенных результатов представлен в [6].

Дифференциальные уравнения возмущенного движения:

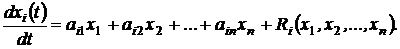
Если отклонения x _i достаточно малы, то, пренебрегая , получим линеаризованные уравнения

 (*),

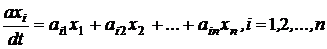называемые уравнениями первого приближения.

Во многих случаях устойчивость движения исследуют по уравнениям первого приближения. Это объясняется не только простотой этого метода, но также и тем, что знания процессов, происходящих в реальных системах, позволяют надежно определять только первые линейные члены. Однако на основании уравнений первого приближения можно дать иногда неверное заключение об устойчивости движения. Поэтому, естественно, возникает вопрос об определении условий, при выполнении которых по уравнениям первого приближения можно дать правильные ответы об устойчивости движения. Эту исключительно важную и принципиальную для теории автоматического управления задачу впервые поставил и решил А. М. Ляпунов.

Системе уравнений (*) соответствует характеристическое уравнение, которое можно записать следующим образом:

 (**)

Из (**) можно найти его корни s _i, где i = 1, 2, …, п, которые в общем случае имеют вид s _i = α _i ± j ω _i, где α _i и ω _i – вещественные и мнимые части корней соответственно.

Для исследования устойчивости систем по их линеаризованным уравнениям принципиально важны следующие теоремы А. М. Ляпунова, которые приведем без доказательства.

Теорема 1. Если вещественные части всех корней s _i характеристического уравнения (**) первого приближения отрицательны, то невозмущенное движение асимптотически устойчиво.

Теорема 2. Если среди корней s _i характеристического уравнения (**) первого приближения имеется хотя бы один корень с положительной вещественной частью, то невозмущенное движение неустойчиво.

Если среди корней характеристического уравнения имеется один или несколько нулевых корней, а вещественные части остальных корней отрицательны, то этот случай называют критическим. Дак показал Ляпунов, в критическом случае устойчивость (неустойчивость) невозмущенного движения не может быть оценена по уравнениям первого приближения, так как она зависит от вида нелинейной функции , и поэтому в этом случае требуется рассмотрение дифференциальных уравнений возмущенного движения в их исходном виде.

Теоремы Ляпунова имеют весьма важное значение, так как они позволяют судить об устойчивости нелинейных систем по их линеаризованным уравнениям (уравнениям первого приближения).

 

Рекомендованная литература по лекции: [6].

 

Лекция 11 «Частотные критерии устойчивости»

11.1 Принцип аргумента.

11.2 Критерий устойчивости Михайлова.

11.3 Критерий устойчивости Найквиста.

 

11.1 Принцип аргумента.

На практике широкое распространение получили частотные критерии устойчивости: критерий Михайлова, критерий Найквиста. И тот, и другой критерии базируются на принципе комплексного аргумента.

Принцип аргумента. Рассмотрим уравнение:

,

здесь l_i – корни данного уравнения

.

Каждому корню l_i на комплексной плоскости соответствует некоторая точка. Если соединить точку с нулем, то можно говорить о векторе.

Длина вектора (рис. 68) равна модулю комплексного числа l_i, а угол, образуемый положительной действительной осью и вектором l_i, есть аргумент комплексного числа l_i.

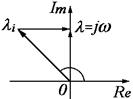
Рисунок 68

 

Придадим l значение j w (l= j w). Считаем движение против часовой стрелки положительным, тогда для корней, находящихся в левой части комплексной плоскости при изменении частоты 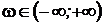, вектор (l-l_i) описывает угол +p (рис. 69).

 

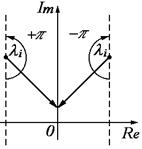
Рисунок 69

 

Для корней, находящихся в правой полуплоскости, вектор (l-l_i) при изменении частоты  опишет угол -p.

Считаем, что порядок системы п -ый, и m корней положительные, значит отрицательных – п - т. Тогда суммарный угол поворота всех векторов составит следующее выражение:

.

 

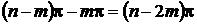11.2 Критерий устойчивости Михайлова.