Суть подхода связана с возможностью выработки некоррелированных оценок в прямом и обратном времени с использованию для их выработки разной совокупности измерений с учетом воздействия на систему на интервалах наблюдения некоррелированных шумов возмущений.
Предположим, что необходимо выработать сглаженную оценку для момента времени 
Предположим, что к этому моменту времени с использованием процедур ФК выработана оптимальная оценка как результат решения задачи фильтрации 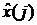 . С другой стороны, оценка вектора состояния может быть найдена как решение задачи фильтрации в обратном времени при обработке массива измерений
. С другой стороны, оценка вектора состояния может быть найдена как решение задачи фильтрации в обратном времени при обработке массива измерений  при использовании описания поведения динамической системы в обратном времени
при использовании описания поведения динамической системы в обратном времени
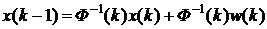
С учетом такого описания алгоритм для получения оценки в обратном времени примет вид

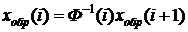
 от
от 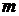 до
до 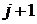 ;
;



Сглаженная оценка с учетом некоррелированности двух оценок получается взвешиванием оценок полученных в прямом и обратном времени
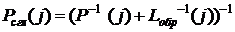 ;
;
 .
.
Подход с использованием уточнения оценок в обратном времени.
Суть подхода заключается в утонении в обратном времени оценки фильтрации с учетом выработки предыдущей сглаженной оценки
Для того, чтобы получить процедуры для выработки сглаженной оценки рассмотрим вектор состояния  и запишем ковариационную матрицу этого вектора
и запишем ковариационную матрицу этого вектора
к моменту обработки измерений  .
.
С учетом связи между векторами

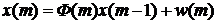
можем записать
 ,
,
 .
.
Обработывая теперь измерение

с использованием процедур ФК получим
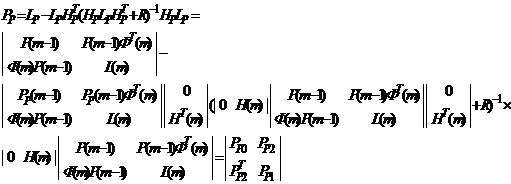
где



Наша цель найти ковариационную матрицу сглаженной оценки

Для этого преобразуем это выражение к виду

Таким образом, ковариационная матрица сглаженной оценки будет равна

Найдем теперь выражение для оценки расширенного вектора состояния

Откуда


Наша задача найти сглаженную оценку  . Для этого преобразуем выражение для эртой оценки к виду
. Для этого преобразуем выражение для эртой оценки к виду

Рассматривая далее сглаженную оценку  как результат обработки измерений
как результат обработки измерений
 ,
, 
Процедуру выработки сглаженных оценок можно продолжить, вырабатывая последовательность сглаженных оценок, при этом выражения примут вид


Очевидно, что три рассмотренных подхода дают одинаковые результаты, при этом точность выработки сглаженных оценок повышается как результат обработки большего числа измерений.
Пример точностей решения задач прогнозирования фильтрации и сглаживания приведен на рисунке





