Базовой основой для вычисления корреляционной функции скалярного процесса является оценка корреляционной функции

где 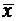 -математическое ожидание.
-математическое ожидание.
Такая оценка является асимптотически несмещенной, т.е

Если математическое ожидание неизвестно используют выражение
 ,
,
в котором  -оценка математического ожидания.
-оценка математического ожидания.

Оценка  также является асимптотически несмещенной оценкой
также является асимптотически несмещенной оценкой
При дискретном количестве наблюдений вычисление интегралов заменяется вычислением сумм

Вычисление корреляционных функций можно провести с использованием программ в Matlab.

На рисунке приведены графики построения выборочной и истинной корреляционных функций случайного процесса с корреляционной функцией 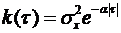 ,
,  ,
, 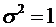 .
.

На этом графике длина реализации составляет 500 сек. при интервале дискретизации 0.01 сек, т.е обрабатывались 50000 наблюдений процесса.
На следующих рисунках длина реализаций была равной 50 и 5 секунд и, следовательно обрабатывались 5000 и 500 наблюдений процесса.

Графики показывают, что точность построения корреляционных функций существенно зависит от длины реализации.
Как правило, представляет интерес аналитическое выражение для корреляционной функции.
С этой целью делается предположение о виде корреляционной функции и проводится ее аппроксимация с использованием МНК.
Оценка спектральной плотности
Один из возможных вариантов может быть основан на получении вначале выборочной корреляционной функции  с последующим применением преобразования Фурье
с последующим применением преобразования Фурье

Следует, однако, иметь в виду, что выборочная функция известна на конечном интервале 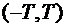 и ее точность на границах интервала существенно ухудшается что может привести к значительным ошибкам в оценке спектральной плотности.
и ее точность на границах интервала существенно ухудшается что может привести к значительным ошибкам в оценке спектральной плотности.
Другой возможный вариант связан с использованием периодограммы, определяемой как

Показано[ Cвешников А.А. Прикладные методы теории случайных функций], что
 ,
,
и поэтому в первом приближении можем считать, что  . Однако, такая оценка не является состоятельной.
. Однако, такая оценка не является состоятельной.
Модификацией этого алгоритма является алгоритм, в котором весь интервал разбивается на  подинтервалов длиной
подинтервалов длиной  , вырабатываются на этом интервале оценки
, вырабатываются на этом интервале оценки

и затем они осредняются

Такая оценка является асимптотически несмещенной и состоятельной [Cвешников]
В общем случае при вычислении оценок в выражение для частных оценок вводят некоторую весовую функцию

где весовая функция обращается в нуль при 
Метод вариации Аллана.
Иногда оценку дисперсии можно определить как
 (*)
(*)
Можно показать, что такая оценка будет несмещенной и состоятельной
Предположим теперь, что имеется  наборов из
наборов из 

И для каждого из них вычисляется среднее значение
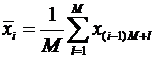 ,
, 
Вариация Аллана определяется следующим образом

Отсюда следует, что вариация Алана представляет собой оценку одной второй дисперсии разности (приращений) средних значений 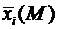 , рассчитанных для каждой группы.
, рассчитанных для каждой группы.
Легко показать, что при  вариация Аллана совпадает с полученной с помощью выражения (*) оценки дисперсии.
вариация Аллана совпадает с полученной с помощью выражения (*) оценки дисперсии.
Вводя знак осреднения по ансамблю  можем записать
можем записать
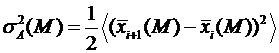 .
.
Для процесса с непрерывным временем определяем
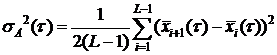
или
 ,
,
где
 -
-
среднее на интервале  .
.
Пример Рассмотрим случайный процесс в виде линейного тренда
 . Найдем вариацию Аллана.
. Найдем вариацию Аллана.
Поскольку
 , то очевидно, что
, то очевидно, что
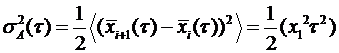
Пример. Найти вариацию Аллана для белого шума интенсивности  .
.
Так как  представляют собой независимые случайные величины с дисперсией
представляют собой независимые случайные величины с дисперсией  , то дисперсия приращений будет равна
, то дисперсия приращений будет равна  .
.
Пример. Найти вариацию Аллана для винеровского процесса

где  -белый шум единичной интенсивности
-белый шум единичной интенсивности
В этом случае дисперсии независимых между собой случайных величин
 определяются как
определяются как  . Таким образом
. Таким образом 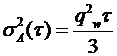 .
.
В работах по вариациям Аллана вводят еще две составляющие: так называемый фликкер шум для которого вариация Алана постоянна и шум квантования, длят которого вариация алана зависит от 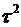 . Эти процессы можно рассматривать как случайные процессы со спектральными плотностями
. Эти процессы можно рассматривать как случайные процессы со спектральными плотностями  и
и  .
.

Выражение при наличии всех упомянутых составляющих запишется в виде


Иногда вариации Аллана изображают в логарифмическом масштабе с типовыми наклонами 

.
Достоинством вариаций Аллана является их использование для нестационарных процессов
Если процессы стационарны можно показать, что имеется соледующая взаимосвязь между вариацией Алана и спектральной плотностью

Действительно, можно записать
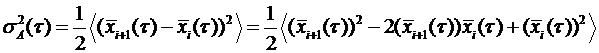
Последнее слагаемое может быть представлено как
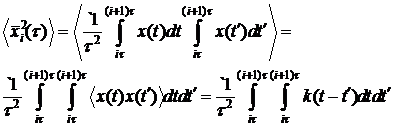
где  корреляционная функция исследуемого процесса.
корреляционная функция исследуемого процесса.
Тогда
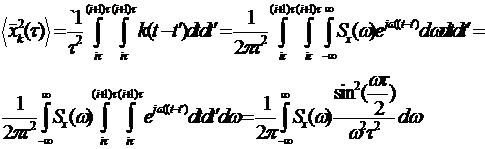
Решение задач сглаживания
Специфика задач сглаживания заключается в выработке оптимальных оценок в момент времени  с использованием всей совокупности полученных к текущему моменту времени измерений.Выделяют три типа задач сглаживания;
с использованием всей совокупности полученных к текущему моменту времени измерений.Выделяют три типа задач сглаживания;
- сглаживание на закрепленном интервале;
-сглаживание в фиксированной точке;
-сглаживание с постоянным запаздыванием.
В задаче сглаживания на закрепленном интервале фиксируется общее количество измерений  и отыскиваются оценки для каждого момента времени
и отыскиваются оценки для каждого момента времени 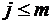 с использованием всей совокупности измерений.
с использованием всей совокупности измерений.
В задаче сглаживания в фиксированной точке фиксируется момент времени на которую вырабатывается оценка с использованием всей совокупности измерений.
В задаче сглаживания с постоянным запаздыванием производится выработка оценки на момент времени, отстоящий на фиксированное число шагов от текущего момента времени
Особенности использования информации приведены на рисунке








