Достаточные условия разложения функции в степенной ряд.
Пусть дан степенной ряд  , радиус сходимости которого R>0. Следовательно, в интервале сходимости ряд сходится к некоторой функции S(x), т.е.
, радиус сходимости которого R>0. Следовательно, в интервале сходимости ряд сходится к некоторой функции S(x), т.е.
S(x)=  =
= 
Задача: Зная функцию S(x), найти коэффициенты  соответствующего степенного ряда.
соответствующего степенного ряда.
Степенной ряд в интервале сходимости можно почленно дифференцировать любое число раз. Поэтому будем иметь:
 ,
, 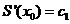 ,
, 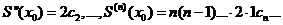

Отсюда вытекает, что необходимым условием разложения функции f(x) в степенной ряд по степеням  является бесконечная дифференцированность функции в точке
является бесконечная дифференцированность функции в точке  , т.е
, т.е

 , где
, где  (1)
(1)
Степенной ряд в соотношении (1) называется рядом Тейлора функции f(x), а  - коэффициенты ряда Тейлора. Если в степенном ряде (1)
- коэффициенты ряда Тейлора. Если в степенном ряде (1)  = 0, то ряд
= 0, то ряд  называется рядом Маклорена для функции f(x)
называется рядом Маклорена для функции f(x)
Однако существуют функции, которые бесконечно дифференцируемы в точке  , но соответствующий степенной ряд сходится к f(x) только в одной точке
, но соответствующий степенной ряд сходится к f(x) только в одной точке  и такие функции представлять степенным рядом не имеет смысла.
и такие функции представлять степенным рядом не имеет смысла.
Для того, чтобы в соотношении (1) имею место равенство в некотором интервале  функция f(x) кроме бесконечной дифференцируемости в точке
функция f(x) кроме бесконечной дифференцируемости в точке  должна удовлетворять дополнительным условиям.
должна удовлетворять дополнительным условиям.
Теорема 1. (Достаточные условия разложения функции в степенной ряд).
Если на отрезке  все производные функции по модулю ограничены одним числом,
все производные функции по модулю ограничены одним числом,  , то f(x) разлагается в ряд Тейлора
, то f(x) разлагается в ряд Тейлора  , который сходится к f(x) на отрезке
, который сходится к f(x) на отрезке 
Пример 1. Разложить в ряд Маклорена функцию у=  .
.
Решение. Функция  бесконечно дифференцируема на всей числовой оси и
бесконечно дифференцируема на всей числовой оси и  .
.
Имеем 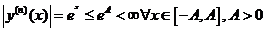 . По теореме 1 функция y=
. По теореме 1 функция y= 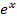 разлагается в ряд Маклорена, который на отрезке [- A, A ] сходится к данной функции.
разлагается в ряд Маклорена, который на отрезке [- A, A ] сходится к данной функции.

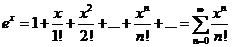 , (-∞,+∞) (2)
, (-∞,+∞) (2)
Так как А- произвольное, то равенство (2) справедливо для любого 
Пример 2. Разложить в ряд Маклорена функцию y=sinx.
Решение. y ’= cosx, y ’’=- sinx, y ’’’=- cosx,  ,…, следовательно
,…, следовательно 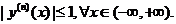 и функция y=sinx разлагается в ряд Маклорена
и функция y=sinx разлагается в ряд Маклорена  , который сходится к функции y=sinx.
, который сходится к функции y=sinx. 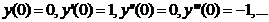
 .
.
Пример 3. Разложить в ряд Маклорена функцию y=cosx.
Решение.
 . Функция y=cosx разлагается в ряд Маклорена, который сходится к функции y=cosx
. Функция y=cosx разлагается в ряд Маклорена, который сходится к функции y=cosx  .
.

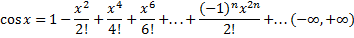
Пример 4. Разложить в ряд Маклорена функцию y=ln(1+x)
Решение. Имеем:  , где|x|<1. Полученное равенство почленно проинтегрируем
, где|x|<1. Полученное равенство почленно проинтегрируем  |x|<1.
|x|<1.
 |x|<1.
|x|<1.
Пример 5. Разложить в ряд Маклорена функцию y=arctgx.
Решение.  |x|<1. Полученное равенство почленно проинтегрируем при |x|<1.
|x|<1. Полученное равенство почленно проинтегрируем при |x|<1. 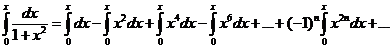 |x|<1.
|x|<1.
 |x|<1.
|x|<1.
Пример 6. Разложить в ряд Маклорена функцию 
Решение. 
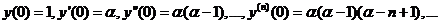
 Можно доказать, что в общем случае последнее равенство справедливо при |x|<1.
Можно доказать, что в общем случае последнее равенство справедливо при |x|<1.
Отметим, что при α натуральном последнее равенство справедливо  , т.к. в левой и правой частях равенства будут многочлены.
, т.к. в левой и правой частях равенства будут многочлены.
Применение степенных рядов.
Пример 7. Вычислить sin1 с точностью  =0,01.
=0,01.
Решение. Имеем. 


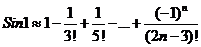 ,при этом ошибка будет равна
,при этом ошибка будет равна 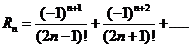
 называется остатком ряда.
называется остатком ряда.  является знакочередующимся рядом, который удовлетворяет всем условиям теоремы Лейбница. Следовательно
является знакочередующимся рядом, который удовлетворяет всем условиям теоремы Лейбница. Следовательно  . Если
. Если 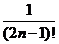 <0.01, то
<0.01, то  <0,01. Подберем наименьшее n, для которого
<0,01. Подберем наименьшее n, для которого 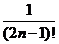 <0.01, n=2
<0.01, n=2  Следовательно,
Следовательно,  , причем ошибка будет меньше 0,01.
, причем ошибка будет меньше 0,01.
Пример 8. Вычислить  с точностью
с точностью  =0,01.
=0,01.
Решение. Неопределенный интеграл  не выражается в элементарных функциях, поэтому формулу Ньютона-Лейбница при вычислении данного интеграла применять нельзя.
не выражается в элементарных функциях, поэтому формулу Ньютона-Лейбница при вычислении данного интеграла применять нельзя.




Последнее равенство проинтегрируем почленно на отрезке [0, 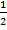 ].
].


 . Ошибка будет равна
. Ошибка будет равна 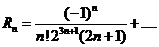 .
.
 является знакочередующимся рядом, который удовлетворяет всем условиям теоремы Лейбница. Следовательно
является знакочередующимся рядом, который удовлетворяет всем условиям теоремы Лейбница. Следовательно 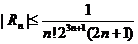 . Если
. Если  <0,01, то и
<0,01, то и  <0,01. Для этого достаточно положить n=2. В самом деле,
<0,01. Для этого достаточно положить n=2. В самом деле,  .
. 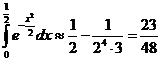 . При этом ошибка будет меньше 0,01.
. При этом ошибка будет меньше 0,01.






