Пусть физическая величина Y, представляет собой дифференцируемую функцию Y = F (X 1, X 2,..., X n) и X 1, X 2,…, X n - независимые результаты прямых измерений значений аргументов X1, X 2,…, X n. Погрешности измерений: абсолютные систематические погрешности ∆ Х 1, ∆ Х 2,…, ∆ Х n; абсолютные среднеквадратические случайные погрешности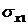 
, 
,…, 
.
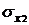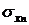Абсолютная систематическая погрешность результата косвенного измерения определяется:
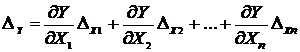. (19)
Абсолютная среднеквадратическая случайная погрешность:
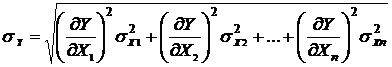, (20)
где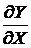 
- частные производные.
Относительные погрешности δ СИСТ и δ СЛ находятся по формулам:
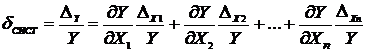; (21)
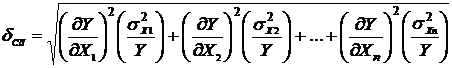. (22)
Примеры
1) Сопротивление Rх измерено с помощью четырехплечего моста и рассчитано по формуле
.
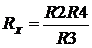Найдите абсолютную D R х и относительную δ R х систематическую погрешности результата измерения, если абсолютные систематические погрешности сопротивлений R 2, R 3, R 4 равны: +1 Ом; -1 Ом; – 1 Ом, соответственно. При этом значения сопротивлений равны: R 2 = 100 Ом; R 3 = 200 Ом; R 4 = 100 Ом.
Решение
Абсолютная систематическая погрешность результата измерения сопротивления R Х находится по формуле (19):
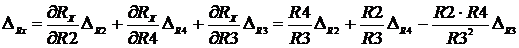
∆R2 = 1 Ом; ∆R3 = -1 Ом; ∆R4 = – 1 Ом
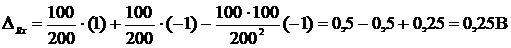
Относительная систематическая погрешность результата измерения сопротивления R Х находится по формуле (21):
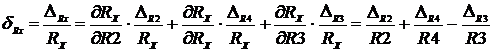
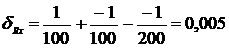
или
.
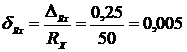
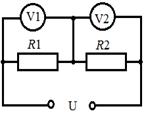2) Определить максимальную абсолютную и относительную погрешности измерения нап-ряжения U в цепи (рис.1). Напряжение U 1 на резисторе R 1, измеренное вольт-метром V1 класса точности 0,5 с верхним пределом измерения 100 В, равно U 1 = 50 В. Напряжение U 2, на резисторе R 2, измеренное вольтметром V2 класса точности 1,5 с верхним пределом измерения 30 В, равно U 2 = 25 В.
Рис. 1
Решение
Находим напряжение U:
U = U 1 + U 2 = 50 + 25 = 75 В.
Находим абсолютную и относительную погрешность измерения напряжения по формуле:
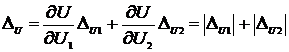
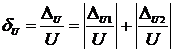
Представление класса точности числом 0,5 и 1,5 означает, что класс точности определяется по приведенной погрешности и погрешность аддитивная, т.е. ∆ U = const.
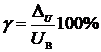и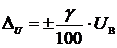 
Получим
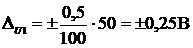
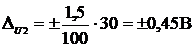
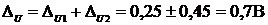
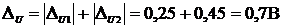
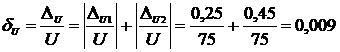
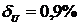
В случае, если переменные Хi или функции от них образуют произведение или частное, удобнее пользоваться следующей формулой для подсчета относительной погрешности результата косвенного измерения:
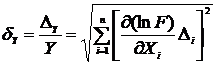, (23)
где ln F есть натуральный логарифм от функции F (X 1, X 2, …, X n).
Пусть функция результата косвенного измерения есть произведение трех величин, полученных из прямых измерений:
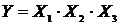
Прологарифмируем функцию Y:
.
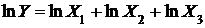Затем дифференцируем ее:
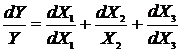
и перейдем к малым конечным приращениям:
.
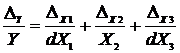Отсюда относительная систематическая погрешность:
.
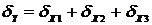Случайная погрешность:
.
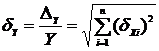Определение параметров переменных напряжений и токов,
