Математическая индукция — в математике — один из методов доказательства. Используется, чтобы доказать истинность некоего утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером 1 — база индукции, а затем доказывается, что если верно утверждение с номером n, то верно и следующее утверждение с номером n + 1 — шаг индукции, или индукционный переход.
Доказательство по индукции наглядно может быть представлено в виде так называемого принципа домино. Пусть какое угодно число косточек домино выставлено в ряд таким образом, что каждая косточка, падая, обязательно опрокидывает следующую за ней косточку (в этом заключается индукционный переход). Тогда, если мы толкнём первую косточку (это база индукции), то все косточки в ряду упадут.
Точное описание
Предположим, что требуется установить справедливость бесконечной последовательности утверждений, занумерованных натуральными числами: 
| Допустим, что 1. Установлено, что P 1 верно. (Это утверждение называется базой индукции.) 2. Для любого n доказано, что если верно Pn, то верно Pn + 1. (Это утверждение называется индукционным переходом.) Тогда все утверждения нашей последовательности верны. |
Логическим основанием для этого метода доказательства служит так называемая аксиома индукции, пятая из аксиом Пеано, определяющих натуральные числа. Верность метода индукции эквивалентна тому, что в любом подмножестве натуральных чисел существует минимальный элемент.
Существует также вариация, так называемый принцип полной математической индукции. Вот его строгая формулировка:
Пусть имеется последовательность утверждений  . Допустим, что
1. Установлено, что P 1 верно.
2. Для любого натурального n доказано, что если верны все  , то верно и Pn + 1. (Это утверждение называется индукционным переходом.)
Тогда все утверждения в этой последовательности верны.
|
Принцип полной математической индукции также эквивалентен аксиоме индукции в аксиомах Пеано.
Примеры
Задача. Доказать, что, каковы бы ни были натуральное n и вещественное q ≠ 1, выполняется равенство
Доказательство. Индукция по n.
База, n = 1:
Переход: предположим, что
тогда
,
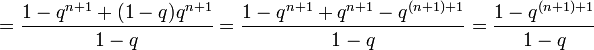что и требовалось доказать.
Комментарий: верность утверждения Pn в этом доказательстве — то же, что верность равенства
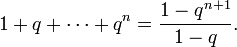
· А. Шень Математическая индукция. МЦНМО, 2004.-36 с. Математическая индукция
- Н. Я. Виленкин Индукция. Комбинаторика. Пособие для учителей. М., Просвещение, 1976.—48 с
- Л. И. Головина, И. М. Яглом Индукция в геометрии, «Популярные лекции по математике», Выпуск 21, Физматгиз 1961.—100 с.
- Р. Курант, Г. Роббинс «Что такое математика?» Глава I, § 2.
- И. С. Соминский Метод математической индукции. «Популярные лекции по математике», Выпуск 3, Издательство «Наука» 1965.—58 с.
