Основные понятия
При помощи матриц очень удобно записывать произвольные системы первой степени (линейные системы). Рассмотрим произвольную линейную систему из m уравнений с n неизвестными.
(1)
Если m=n, то будем называть систему квадратной n-го порядка, если m<n - укороченной (с такими системами встречаются в экономике), при m>n - удлиненной (такие системы встречаются в геодезии).
Матричный метод решения систем линейных уравнений
Представим систему линейных уравнений с n неизвестными в матричном виде. Пусть
А – матрица, составленная из коэффициентов при неизвестных (её называют основной матрицей системы),
Х – матрица-столбец неизвестных
В – матрица-столбец свободных членов.
Тогда систему (1) можно записать при помощи этих матриц следующим образом:
A× Х=В (2)
Действительно,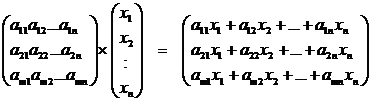 
Уравнение (2) равносильно системе (1).
Матричная запись системы (1) аналогична записи уравнения с одним неизвестным a x=b, решением которого при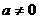 
будет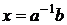 
. Естественно поставить аналогичный вопрос для решения матричного уравнения A × Х=В.
Если матрица А – невырожденная, т.е. detA ≠ 0 и А имеет единственную обратную матрицу А-1, то Х = А-1 В – решение системы уравнений (1).
Пример.
Решите систему матричным методом
Решение:
Ответ: (1; 1; 1)
Решение систем линейных уравнение по формулам Крамера
Теорема. Если определитель системы n линейных уравнений с n неизвестными не равен нулю, то система совместна и имеет единственное решение, которое находится по следующим формулам:
Х1= 
, X2 = 
,…, xn= 
, где
D – определитель системы
Dn – определитель, который получается из определителя системы путем замены только n-го столбца столбцом свободных коэффициентов системы.
Рассматривают различные случаи:
1. Система является совместной и определённой, если её определитель D≠0.
2. Система является совместной, но неопределённой, если все её определители равны нулю:
D = D1 = D2 =…= Dn = 0
3.Система несовместна, если только определитель системы D=0
Пример.
Решите систему по формулам Крамера
Решение:
Определитель системы вычислим по правилу треугольников
D= 
= 42+36+2-(-21+36-4) = 69 ≠ 0
D1, D2, D3 вычислим по формуле Лапласа.
D1=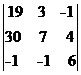 
= (определитель разложим по первому столбцу)
=19 ∙ 
- 30 ∙ 
- 1 ∙ 
= 19∙(42+4)-30∙(18-1)-1∙(12+7) = 19∙46-30∙17-19 = 345
D2 = 
= (разложим по второму столбцу)
= -19 ∙ 
+30 ∙ 
+1·∙ 
= -19∙(12-12)+30∙(6+3)+(4+2) = 30·9+6 = 276
D3= 
= (разложим по третьему столбцу)
= 19 ∙ 
- 30 ∙ 
-1 ∙ 
= 19∙23)-30∙10)-1·1 = -138
Тогда
х1= 
=5
х2= 
=4
х3= 
= -2
Ответ: (5; 4; -2).
КОНТРОЛЬНЫЕ ЗАДАНИЯ
Вопросы для самопроверки
1. Что называется матрицей?
2. Какие виды матрицы называются равными?
3. Что называется определителем второго, третьего, 
- ого порядков? Перечислите основные свойства определителей.
4. Что называется минором, алгебраическим дополнением элемента определителя?
5. Какие матрицы называются эквивалентными?
6. Перечислите элементарные преобразователи матриц.
7. Что называется рангом матрицы?
8. Как найти обратную матрицу?
9. Напишите формулы Крамера для решения систем линейных уравнений. В каких случаях их можно использовать?
