ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«МОСКОВСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ ВЕТЕРИНАРНОЙ МЕДИЦИНЫ И БИОТЕХНОЛОГИИ ИМ. К.И. СКРЯБИНА»
_______________________________________________________________
Джугели Т.П., Кишкинова О.А., Кутликова И.В., Федькина Т.В.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПО
ЛИНЕЙНОЙ АЛГЕБРЕ
Москва 2011
УДК
Джугели, Т.П., Кишкинова, О.А., Кутликова, И.В., Федькина, Т.В. Линейная алгебра: учеб.-метод. указ. / Т.П. Джугели, О.А. Кишкинова, И.В. Кутликова, Т.В. Федькина. – М.: ФГОУ ВПО МГАВМиБ им. К.И. Скрябина, 2011. – 24 с.
В методических указаниях приведены необходимые теоретические сведения и формулы, даны решения типовых задач, приведены задачи для самостоятельного решения контрольной работы по разделу математики «Линейная алгебра».
Рекомендованы для студентов обучающихся по специальностям:
020400 бакалавр «Биологии», 240700 бакалавр «Биотехнологии»,
111900.62 бакалавр «Ветсанэкспертизы», 260200 бакалавр «Продуктов питания животного происхождения», 260100 бакалавр «Продуктов питания из растительного сырья», 100800 «Товароведение» (очная и заочная форма обучения), 111100 бакалавр «Зоотехнии» (очная и заочная форма обучения).
Рецензент: доцент кафедры Биофизики и физики ФГБОУ ВПО МГАВМиБ
им. К.И. Скрябина А.А. Олешкевич.
Утверждены на заседании учебно-методической комиссии факультета ветеринарной медицины ФГОУ ВПО МГАВМиБ им. К.И. Скрябина (протокол № 6 от 25 февраля 2011 г.)
ВВЕДЕНИЕ
Целью настоящих указаний по Линейной алгебре является познакомить студентов с теоретическим материалом, необходимым для изучения физики, химии, экономики, генетики и биометрии и подготовить высококвалифицированных специалистов в области ветеринарии.
В методических указаниях рассмотрены понятия матрицы и определителя, действия над матрицами, свойства определителей, правила вычислений определителей, методы решения систем линейных уравнений, а также приведены варианты индивидуальной контрольной работы студентов и тестовые задания по данному разделу дисциплины.
Одной из основных форм работы студента является самостоятельная работа над учебным материалом. Она состоит из непрерывной работы по изучению теоретического материала, по выполнению текущих заданий и контрольных работ. Результативность самостоятельной работы обеспечивается эффективной системой контроля, которая включает в себя опросы студентов по содержанию лекций, тестирование по отдельным разделам дисциплины, контрольные работы.
При выполнении и оформлении домашней контрольной работы по Линейной алгебре студент должен придерживаться следующих правил:
а) в заголовке контрольной работы должны быть ясно выписаны фамилия студента, его инициалы, номер задания;
б) контрольную работу следует выполнять в особой тетради, обязательно чернилами(не красными), с оставлением полей для замечаний преподавателя;
в) решения контрольных задач следует располагать в порядке номеров, указанных в заданиях; перед решением каждой задачи надо выписывать полностью ее условие.
Контрольная работа, выполненная небрежно, без промежуточных вычислений, с пропуском задач и без соблюдения изложенных выше правил, возвращается обратно для переработки. Контрольная работа, выполненная не по своему варианту, не проверяется. Номер варианта соответствует номеру студента в списке группы.
МАТРИЦЫ
Основные понятия
Матрицей размера m  n называется прямоугольная таблица чисел, содержащая m строк одинаковой длины (или n столбцов одинаковой длины).
n называется прямоугольная таблица чисел, содержащая m строк одинаковой длины (или n столбцов одинаковой длины).
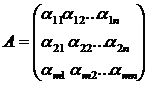
Матрицы обозначают большими латинскими буквами А, В, С, D …
При этом пишут A=(aij).
Числа aij (i=1, …, m, j=1…n) называются элементами матрицы А.
Матрица размером 3  2 имеет ид
2 имеет ид 
Первый индекс указывает номер строки, второй – номер столбца.
Всего в матрице m  n м имеется mn элементов.
n м имеется mn элементов.
Главной диагональю в матрице n-ого порядка называется линия, соединяющая элементы с одинаковыми индексами.
Побочной диагональю в матрице n-ого порядка называется линия, идущая из левого нижнего угла в правый верхний угол.
Классификация матриц
1. Матрицы называются равными при совпадении у них соответствующих элементов и обозначаются А=В.
2. Матрица, у которой число строк равно числу столбцов называется квадратной. Квадратную матрицу размера n  n называют матрицей n–го порядка.
n называют матрицей n–го порядка.
3. Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной.
4. Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной. Обозначается буквой Е.
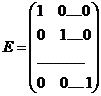
5. Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали равны нулю.
При этом выделяются два типа треугольных матриц:
1) 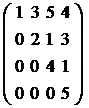 - нижнетреугольная матрица.
- нижнетреугольная матрица.
2)  - верхнетреугольная матрица.
- верхнетреугольная матрица.
6. Матрица, все элементы которой равны нулю, называется нулевой. Обозначается буквой О.
7. Матрица, содержащая один столбец или одну строку, называется вектором (или вектор – столбец, или вектор - строка).
8. Матрица Ат называется транспонированной к А, если в матрице А строки заменены на столбцы соответствующих номеров.
9. Матрица А-1 называется обратной матрице А, если выполняется условие

10. Матрицы называются одноименными, если они имеют одинаковый размер.
Элементарные преобразования матриц
1. Перестановка местами двух параллельных рядов матрицы.
2. Умножение всех элементов ряда матрицы на число отличное от нуля.
3. Прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.
Две матрицы А и В называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований и обозначается А ~ В. 
При помощи элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю. Такую матрицу называют канонической.

Действия над матрицами
Сумма матриц определена для 2-х одноименных матриц.
Суммой 2-х матриц одинакового размера 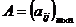 и В=(вij)
и В=(вij)  называется матрица С=
называется матрица С=  , где
, где  .
.
При этом пишут С=А+В
Аналогично определяется разность матриц, А - В.
Пример.
Найти А + В, если А=  , В=
, В= 
Решение:
А + В=С

Ответ: С= 
Произведением матрицы 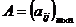 на число
на число 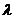
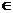 R называется новая матрица
R называется новая матрица 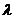 ∙А определяемая формулой
∙А определяемая формулой  или
или
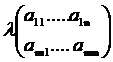 =
= 
Пример.
Найти А∙ 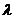 , если
, если

Решение:
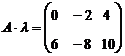
Ответ: С= 
Операция сложения матриц и умножение матрицы на число обладают следующими свойствами:
А, В, С – матрицы, α и β – числа.
1. А+В=В+А 5. 1·А=А
2. А+(В+С)=(А+В)+С 6. α·(А+В)= αА+ αВ
3. А+О=А 7. (α+β)·А= αА+ βА
4. А-А=0 8. α·(βА)=(αβ)·А,
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы. Такие матрицы называются согласованными (n  m и m
m и m  k).
k).

Произведением 2-х согласованных матриц  и
и  называется матрица
называется матрица  размера n
размера n  k, элементы которой вычисляются по формуле:
k, элементы которой вычисляются по формуле:
C  =a
=a  ∙b
∙b  +a
+a 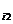 ∙b
∙b 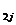 +….+a
+….+a  b
b 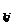 +…..+a
+…..+a  ∙b
∙b 
Таким образом, элементом новой матрицы является  , который равен сумме произведений элементов
, который равен сумме произведений элементов  строки первой матрицы на соответствующие элементы
строки первой матрицы на соответствующие элементы  столбца второй матрицы.
столбца второй матрицы.
Возможно умножение матрицы на вектор-столбец справа и на вектор-строку слева.
Примеры.
1. Найти произведени е А∙ В матриц, если
А= 
Решение:
С=А∙В

Ответ: С= 
2. Найти произведени е А∙ В матриц, если
А= 
В= 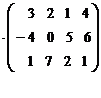
Решение:
(9 2 3) ∙  = (9∙3+2∙(-4)+3∙1; 9∙2+2∙0+3∙7; 9∙1+2∙5+3∙2;
= (9∙3+2∙(-4)+3∙1; 9∙2+2∙0+3∙7; 9∙1+2∙5+3∙2;
9∙4+2∙6+3∙1=(22 29 25 51)
Ответ: С=(22 29 25 51)
3. Найти произведени е А∙ В матриц, если

Решение:
С=А∙В
 ∙
∙  =
= 
 =
= 
Ответ: С= 
Умножение матриц обладает следующими свойствами:
1. А × О = О 4. α (АВ) = (αА)  В = А × (αВ)
В = А × (αВ)
2. А × Е = А 5. АВС = (АВ)  С = А
С = А  (ВС)
(ВС)
3. А × В ≠ В  А 6. А × (В + С) = АВ + АС,
А 6. А × (В + С) = АВ + АС,
ОПРЕДЕЛИТЕЛИ
Основные понятия
Каждой квадратной матрице А n-ого прядка ставится в соответствии действительноечисло, обозначаемое символом det A или  А, называемое определителем или детерминантом квадратной матрицы А и вычисляемое следующим образом:
А, называемое определителем или детерминантом квадратной матрицы А и вычисляемое следующим образом:
1. n = 1
А = (a11); det A = a11
2. n = 2



3. n = 3



Пример.
Найти определитель матрицы А, если
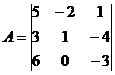
Решение: 
Ответ: detA=9
5. Если n>3, то  А вычисляется по специальному правилу, которое укажем далее.
А вычисляется по специальному правилу, которое укажем далее.
Свойства определителей
1. Транспонирование определителя, т.е. замена строк столбцами и наоборот, не меняет его значения.

2. Перестановка любых двух строк (столбцов), меняет только знак определителя.
D = - D
3. Общий множитель всех элементов одной строки (столбца) может быть вынесен за знак определителя.

4. Если соответствующие элементы двух строк (столбцов) равны или пропорциональны, то определитель равен 0.
5. Если элементы какой-либо строки (столбца) определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.
6. Определитель не изменится, если к элементам одной строки (столбца) прибавить соответствующие элементы параллельной строки (столбца), умноженные на любое число.
Минор элемента
Пусть дана квадратная матрица А=(а  )
) 
Минором некоторого элемента aij определителя n-го порядка матрицы А называется определитель (n-1)–го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент и обозначается Мij.
Пример.
Найти минор элемента a23 данного определителя.

Решение:



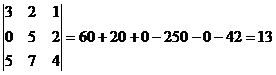 |
M23 =
Ответ: М 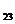 =13.
=13.
2.4. Алгебраическое дополнение
Алгебраическим дополнением A  данного элемента определителя называется его минор Мij, умноженный на
данного элемента определителя называется его минор Мij, умноженный на  , где i и j – номера строки и столбца на пересечении которых расположен этот элемент
, где i и j – номера строки и столбца на пересечении которых расположен этот элемент 
Пример.
Найти алгебраическое дополнение элемента a23 данного определителя.



Решение:

 =-13
=-13
А31=(-1)  М31=5
М31=5
А14=(-1) 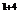 М14=-11
М14=-11
Ответ: А  =-13; А
=-13; А  =5; А
=5; А  =-11
=-11
Формула Лапласа
Теорема. Определитель равен сумме произведений элементов всякой его строки (столбца) на их алгебраические дополнения.
Пример.
Найти определитель матрицы путем разложения по элементам 1 столбца, если
А= 
Решение:
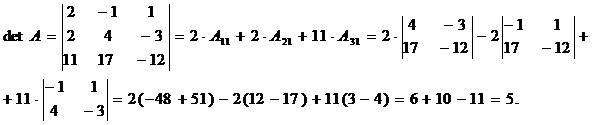
Ответ: detA=5.
Обратная матрица
Квадратная матрица А называется невырожденной, если det A не равен 0. В противном случае (det A равен 0) матрица А называется вырожденной.
Матрица А-1 называется обратной квадратной матрице А, если выполняется условие:
 ,
,
где Е – единичная матрица того же порядка, что и матрица А. Матрица А-1 имеет те же размеры, что и матрица А.
Теорема. Всякая невырожденная матрица имеет обратную.
Союзной к матрице А называется матрица вида:
 ,
,
где  - алгебраическое дополнение элемента
- алгебраическое дополнение элемента  данной матрицы А (оно определяется так же, как и алгебраическое дополнение элемента определителя).
данной матрицы А (оно определяется так же, как и алгебраическое дополнение элемента определителя).
Алгоритм нахождения обратной матрицы
1. Найти определитель матрицы А.
det А ≠ 0
2. Составить матрицу А* из алгебраических дополнений элементов А.
3. Транспонировать матрицу А* для получения союзной матрицы А*т
4. Домножить матрицу А*т на 1/detA для получения обратной матрицы А-1.
Свойства обратной матрицы
1.  .
.
2.  .
.
3.  .
.
Пример:
Найти обратную матрицу для матрицы
А= 
Решение:
Найдем определитель матрицы
detA= 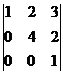
Разложим этот определитель по элементам третьей строки, т.е.
detA=a 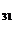 ∙A
∙A  +a
+a 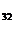 ∙A
∙A 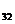 +a
+a  ∙A
∙A  =0+0+1∙
=0+0+1∙  =4
=4
A 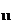 =
= 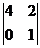 =4, А
=4, А 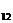 =-
=-  =0, А
=0, А 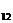 =-
=-  =0, А
=0, А 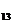 =
=  =0
=0
A  =
=  =-2, А
=-2, А  =
=  =1, А
=1, А  =-
=-  =0, А
=0, А  =
= 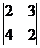 =-8,
=-8,
А 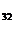 =-
=-  =-2, А
=-2, А  =
=  =4
=4
Следовательно:
 =
= 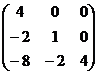
Далее:  =
= 
Находим:
А  =1/4∙
=1/4∙  =
= 
Делаем проверку
А∙А  =
=  ∙
∙  =
= 
Ответ: А  =
= 
Ранг матрицы
Рангом матрицы А называется наивысший порядок отличного от нуля минора этой матрицы.
Ранг матрицы А обозначается rangA или r(A).
Из определения следует:
1. Ранг матрицы А  не превосходит меньшего из ее размеров.
не превосходит меньшего из ее размеров.
2. r(А)=0 тогда и только тогда, когда все элементы матрицы равны 0.
3. Для квадратной матрицы n-ого порядка r(А)=n, тогда и только, когда матрица А – невырожденная.
Пример.
Найти ранг матрицы
А= 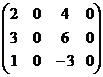
Решение:
Все миноры 3-ого порядка равны нулю. Есть минор 2-го порядка, отличный от нуля 
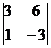 =-15
=-15  . Значит, ранг данной матрицы равен двум (rang А=2)
. Значит, ранг данной матрицы равен двум (rang А=2)
Ответ: r(А)=2
Ранг канонической матрицы равен числу единиц на главной диагонали. На этом основан один из способов вычисления ранга матрицы.
Пример.
Найти ранг матрицы путем элементарных преобразований
А= 
Решение:
 ~
~ 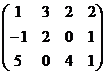 ~
~  ~
~  ~
~
~  ~
~ 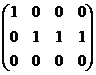 ~
~ 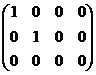
Ранг матрицы равен количеству ненулевых строк, следовательно, ранг данной матрицы равен двум (rang A=2).
Ответ: r(A)=2
Свойства ранга матрицы
1. При транспонировании матрицы ее ранг не меняется.
2. Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится.
3. Ранг матрицы не изменяется при элементарных преобразованиях матрицы.






