Если в общем уравнении прямой (5) В ¹0, то, решив его относительно у, получим уравнение вида
| y = kx + b | (6) |
здесь k =– A / B, b =–С/В. Его называют уравнением с угловым коэффициентом, поскольку k= tg a, где a - угол, образованный прямой с положительным направлением оси Ох. Свободный член уравнения(6) b равен ординате точки пересечения прямой с осью Оу.
Уравнение прямой, проходящей через заданную точку М(х0;у0) в заданном направлении

| (7) |
Уравнение прямой в отрезках
Если в общем уравнении прямой (5) С ¹0, то разделив все его члены на С, получим уравнение вида
| x / a + y / b =1 | (8) |
где а =–С/А, b =–С/В.
Его называют уравнением прямой в отрезках. В (8) а является абсциссой точки пересечения прямой с осью Ох, а b – ординатой точки пересечения прямой с осью Оу. Поэтому а и b называют отрезками прямой на осях координат.
Уравнение прямой, проходящей через две заданные точки М1(x1; y1) и М2(x2; y2)

| (9) |
Пример 1.
Составить уравнение прямой, отсекающей на оси ординат отрезок b =–2 и имеющей угловой коэффициент k =3.
Решение:
Применяя формулу (6), запишем уравнение искомой прямой:
у =3 х –2.
Ответ: у =3 х –2.
Пример 2.
Составить уравнение прямой, отсекающей на осях координат отрезки а =2,5 и b =1,5.
Решение:
Воспользовавшись формулой (8) имеем:
х /2,5+у/1,5=1.
Приведем это уравнение к общему виду:
(2/5)х+(2/3)у=1 или 6х+10у–15=0.
Ответ: 6х+10у–15=0.
Пример 3.
Дано общее уравнение прямой 2х–5у+10=0.
Написать: 1) уравнение с угловым коэффициентом;
2) уравнение в отрезках;
3) построить прямую.
Решение:
1) Разрешив уравнение относительно у, получим уравнение с угловым коэффициентом:
5у=2х+10 или у =(2/5)х+2.
Здесь k =2/5; b =2.
2) Перенесем свободный член уравнения в правую часть и разделим обе части на (–10):
2х/(–10)–5у/(–10)=1.
Здесь а =–5; b =2.
3) Построим прямую:

Пример 4.
Составить уравнение прямой, проходящей через начало координат и точку М (–1;5).
Решение:
Воспользуемся формулой (9)
 ;
;
– y=5 x;
5 x+ y=0 – общее уравнение прямой.
Ответ: 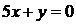
Пример 5.
Составить уравнение прямой, проходящей через точки А (2;–3) и
В (–4;5).
Решение:
Применяя формулу (9) и подставляя х 1=2, у1=–3, х2=–4, у2=5, получим:
(у–(–3))/(5–(–3))=(х–2)/(–4–2) или (у+3)/8=(х–2)/(–6), 4(х–2)=–3(у+3).
Искомое уравнение имеет вид 4х+3у+1=0.
Ответ: 4х+3у+1=0
Пример 6.
Даны вершины треугольника А (–1;1), В(5;7), С(–9;3).
Найти уравнения медиан А D, BE, CN.
Решение:
Найдем сначала координаты точки D – середины стороны ВС по формуле (4):
х =(5–9)/2=–2;
у =(7+3)/2=5,
т. е. D (–2; 5).
Уравнение медианы AD находится с помощью уравнения прямой, проходящей через две точки:
(у –1)/(5–1)=(х +1)/(–2+1) или (у –1)/4=(х +1)/(–1),
т. е. 4 х + у +3=0.
Ответ: Уравнение медианы AD 4х+у+3=0.
Уравнения медиан ВЕ и CN находятся аналогично.
Угол между двумя прямыми
Угол между прямыми y1= k 1 x + b 1 и y2 = k 2 x + b 2 определяется по формуле
| tg a =(k 2 – k 1)/(1+ k 2 k 1) | (10) |
Условие параллельности прямых
Две прямые параллельны тогда и только тогда, когда равны их угловые коэффициенты, т.е.
k 2= k 1.






