2.4.1 Понятие многомерной выборки
Во время статистических наблюдений для каждого объекта в ряде случаев требуется измерить значения сразу нескольких признаков (характеристик), например, xi, yi , и др. Таким образом, получается многомерная выборка.
Смысл обработки многомерных выборок состоит в том, чтобы установить связи между признаками. Связи могут быть строго функциональными, то есть каждому значению одной величины соответствует только одно, определённое значение другой величины.
Связь между случайными величинами часто носит случайный характер. Такая связь (зависимость) называется стохастической или статистической, если изменение одной величины вызывает изменение распределения другой величины. Если среднее значение одной случайной величины функционально зависит от значений другой случайной величины, то такая статистическая зависимость называется корреляционной.
Далее будем рассматривать в основном двумерные выборки.
2.4.2 Эмпирическая формула (зависимость)
Величины X и Y могут быть функционально зависимы, но на процесс измерения их значений влияют разные, в основном случайные, факторы. Установить по результатам измерений вид фактической зависимости не так просто.
Результаты измерений, наблюдений обычно фиксируют в таблице наблюдений (таблица 5):
Таблица 5
| X | x1 | x2 | x3 | … | xn |
| Y | y1 | y2 | y3 | … | yn |
Представим эти результаты на координатной плоскости (корреляционном поле) в виде точек, координатами которых являются парные значения признаков X и Y одного объекта (xi, yi), i = 1, …, n (рисунок 29).
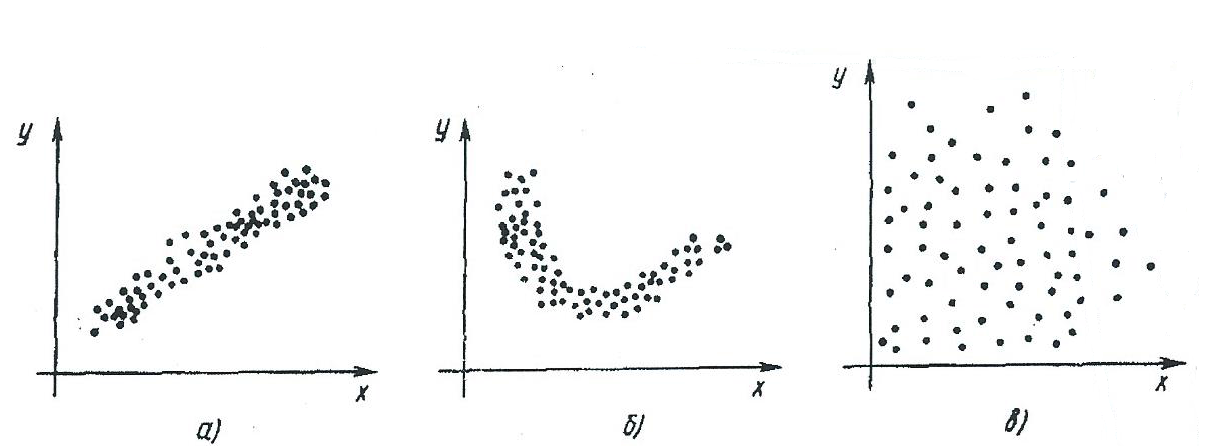
Рисунок 29. Представление двумерной выборки на корреляционном поле
Из рисунка 29 видно, что в случае a) следует искать линейную зависимость, в случае б) – нелинейную зависимость, а в случае в) вряд ли какая-то зависимость существует.
Конкретный вид функциональной зависимости между величинами X и Y, установленный по двумерной выборке, называют эмпирической формулой (зависимостью, моделью). Если построить график (линию) эмпирической формулы на корреляционном поле, то он не обязан проходить через все точки (xi, yi) выборки. а должен быть наилучшим приближением к этим точкам. Расстояние этих точек от графика должно быть в среднем минимальным. При этом предпочтение отдаётся эмпирической формуле, имеющей более простой, причём плавный, вид.
Простейшим видом эмпирической формулы является линейная функция
y = ax + b (2.57)
Задача установления эмпирической формулы заключается в вычислении по выборке коэффициентов a и b в формуле (2.57). Аналогично можно получить коэффициенты и других функций для представления результатов наблюдений, например y = ax 2 + bx + c и т. д.
2.4.3 Нахождение линейной эмпирической формулы
Для получения линейной эмпирической формулы (2.57) имеется несколько способов.
В простейшем из них, по сути графическом методе “натянутой нити”, все результаты измерений изображают в виде точек на корреляционном поле (см. рисунок 29). Далее следует мысленно натянуть через все эти точки нить так, чтобы по обе стороны осталось примерно одинаковое количество точек (точнее, чтобы их суммарные отклонения в обе стороны были примерно, “на глаз” равными). Возьмём на прямой, совпадающей с направлением нити, две точки с координатами (x 1, y 1) и
(x 2, y 2), которые не обязательно должны присутствовать в выборке, но быть достаточно удалёнными друг от друга (рисунок 30).

Рисунок 30. Метод “натянутой нити” и метод “центров масс”
Подставив найденные координаты в формулу (2.57), имеем систему линейных уравнений:
 (2.58)
(2.58)
где неизвестными являются коэффициенты a и b. Решая систему (2.58), получаем эмпирическую формулу (2.57). Таким образом получается прямая линия, приближенно представляющая результаты наблюдений, измерений.
Две характерные точки можно получить точнее. Надо разделить массив точек по x примерно на две равные группы (рис. 30)и для каждой из них найти координаты их «центров масс» ( по формулам:
по формулам:

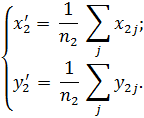
Записывая систему уравнений, аналогичную (2.58), получаем неизвестные коэффициенты a и b для эмпирической формулы (2.57).
Этот способ построения прямой (координаты «центров масс” на рисунке 30 показаны *) назовём методом “центров масс”. Здесь не нужны приближенные мысленные построения “на глаз”, это повышает точность.
Коэффициенты формулы (2.57), найденные разными методами, не обязаны совпадать.
Задача 2.13
Рассмотрим пример получения линейной эмпирической формулы методом “центров масс”для следующих результатов наблюдений:
Таблица 6
| х | 1,0 | 1,4 | 3,0 | 4,0 | 6,0 | 8,0 | 10 |
| у | 4,5 | 7,0 | 10,4 | 15 | 24 | 25 | 35 |
Решение: Так как число точек (пар) – нечётное, возьмём для 1-ой группы первые 4 значения (x, y), а для 2-ой - оставшиеся 3 значения. Получаем координаты двух “центров масс”:
 = 2,35;
= 2,35;  = 8,0;
= 8,0;
 = 9,23;
= 9,23;  = 28.
= 28.
Решая систему (2.58), получаем: а = 3,32; в = 1,43.
Таким образом, эмпирическая (линейная) формула имеет вид:

Позднее будет рассмотрен самый точный, но и более трудоёмкий метод наименьших квадратов. Метод “натянутой нити” самый простой, но и самый неточный.
2.4.4 Корреляционная таблица
По таблице наблюдений (смотри таблицу 5) невозможно судить о распределении случайных величин X и Y, а также об их общем распределении. По одномерной выборке мы составляли вариационные ряды, а в двумерном случае составляют корреляционные таблицы.
Все полученные (в опытах) варианты (значения) или интервалы значений одной случайной величины (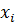 ) записывают в первый столбец корреляционной таблицы, а все варианты или интервалы другой случайной величины (
) записывают в первый столбец корреляционной таблицы, а все варианты или интервалы другой случайной величины (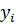 ) – в первую строку. По каждой паре значений (
) – в первую строку. По каждой паре значений (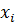 ,
, 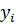 ) решают, в какую строку попадает первое значение (
) решают, в какую строку попадает первое значение (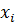 ) и в какой столбец – другое (
) и в какой столбец – другое (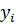 ). Затем подсчитываем получившееся при этом число значений в каждой из клеток таблицы и заменяем их соответствующим числом
). Затем подсчитываем получившееся при этом число значений в каждой из клеток таблицы и заменяем их соответствующим числом 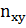 . Далее, суммируя числа
. Далее, суммируя числа 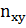 по строкам и столбцам, находим частоты
по строкам и столбцам, находим частоты  . В корреляционной таблице могут остаться пустые клетки, это означает, что в выборке отсутствуют соответствующие сочетания значений X и Y.
. В корреляционной таблице могут остаться пустые клетки, это означает, что в выборке отсутствуют соответствующие сочетания значений X и Y.
2.4.5 Регрессия
Если в двумерной случайной величине зафиксировать значение одной случайной величины, например, Y = y; то совокупность соответствующих значений другой случайной величины Х можно рассматривать как отдельную (одномерную) случайную величину со своим законом распределения и своими числовыми характеристиками распределения, которые, как и само распределение, называют условными (например, условное среднее).
Если рассмотреть условные средние значения одной случайной величины при всех значениях другой случайной величины, то получим функции, называемые функциями регрессии. Если функции регрессии известны, то можно по значению одной случайной величины прогнозировать значение другой случайной величины.
Обычно конкретный вид функции регрессии неизвестен и определяется по двумерной выборке. При этом используем те же методы, что и при установлении эмпирической формулы.
2.4.6 Эмпирическая регрессия
Эмпирическая регрессия показывает зависимость условного среднего арифметического одной случайной величины от значений другой случайной величины. Все вычисления выполняют по корреляционной таблице.
Если при составлении корреляционной таблицы использованы интервалы значений случайной величины, то представителями интервалов являются их середины.
Таким образом, получаются пары чисел: значения одной случайной величины и условные средние арифметические другой случайной величины. Эти пары чисел можно изобразить в виде точек на координатной плоскости (корреляционное поле). Проводя через эти точки плавную (усредненную по определенному правилу) линию, получаем график (линию) эмпирической регрессии  (
( ).
).
2.4.7 Метод наименьших квадратов (МНК)
Будем искать функции регрессии в самом простом – линейном виде. Для наблюдаемых случайных величин x и y можно рассматривать функции эмпирической регрессии двух видов:
 = f ̃(x) =
= f ̃(x) =  x +
x +  ; (2.67)
; (2.67)
или x ̃(y) = g (y) = 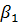 y +
y +  . (2.68)
. (2.68)
Графики их обычно не совпадают, так как коэффициенты регрессии являются случайными величинами.
Обе эти зависимости могут быть использованы равноправно.
Для определения этих функций, то есть коэффициентов  ,
,  ,
, 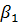 ,
,  , можно использовать приближенные методы, указанные в пункте 2.4.3.
, можно использовать приближенные методы, указанные в пункте 2.4.3.
Рассмотрим наиболее точный способ – метод наименьших квадратов. Находим отклонения (невязки) между измеренными 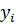 и вычисленными (по функциям регрессии) значениями Y в каждой точке
и вычисленными (по функциям регрессии) значениями Y в каждой точке 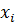 :
:
 =
= 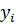 -
-  -
-  -
-  , i = 1, …, n, где
, i = 1, …, n, где 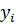 - измеренные (фактические) значения,
- измеренные (фактические) значения,
 рассчитанные (по 2.67) значения.
рассчитанные (по 2.67) значения.
В методе наименьших квадратов коэффициенты a1 и a0 определяют, исходя из критерия - требования минимума суммы квадратов отклонений  :
:
T =  =
=  -
-  -
-  = min. (2.69)
= min. (2.69)
Сумма (2.69) является функцией неизвестных коэффициентов  и
и  (значения
(значения  и
и 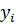 - известны). Для нахождения минимума запишем частные производные от суммы Т по этим коэффициентам:
- известны). Для нахождения минимума запишем частные производные от суммы Т по этим коэффициентам:
 =
=  ;
;
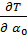 =
= 
Исходя из необходимого условия минимума (экстремума), приравняем эти частные производные нулю и получим систему линейных, так называемых нормальных, уравнений для определения коэффициентов  и
и  . Решая эту систему, находим коэффициенты линейной регрессии:
. Решая эту систему, находим коэффициенты линейной регрессии:
 =
=  -
-  ;
;  =
=  ; (2.70)
; (2.70)
где  =
=  ,
,  =
=  =
=  ,
,  =
= 
 - (
- (  .
.
Коэффициенты линейной регрессии часто вычисляют с помощью коэффициента линейной корреляции
r =  , (2.71)
, (2.71)
где часть величин определена выше, а

Отсюда, для коэффициентов  , с учетом (2.71), получаем
, с учетом (2.71), получаем
 =
=  -
-  . (2.72)
. (2.72)
Заменяя в этих формулах величины, связанные с х, соответствующими величинами, зависящими от y, и, наоборот, получим аналогичные формулы для вычисления коэффициентов 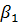 и
и  функции линейной регрессии х = g (y) [формула (2.68)]:
функции линейной регрессии х = g (y) [формула (2.68)]:
 . (2.73)
. (2.73)
Формулы (2.72) и (2.73) пригодны для вычислений с помощью ЭВМ или микрокалькулятора.
По найденным коэффициентам можно записать функции регрессии [см. формулы (2.67) и (2.68)] и построить их графики. Если все вычисления сделаны корректно и графики построены точно, то они пересекаются в некоторой точке с координатами (  ).
).
Задача 2.14 (на дом)
С помощью МНК (можно использовать программу Excel) найти функцию линейной регрессии  для прежних исходных данных из табл. 6 задачи 2.13. Построить график (линию) регрессии с исходными точками. Найти значение коэффициента линейной корреляции r.
для прежних исходных данных из табл. 6 задачи 2.13. Построить график (линию) регрессии с исходными точками. Найти значение коэффициента линейной корреляции r.
2.4.8 Коэффициент линейной корреляции
Линейная функция регрессии – самый простой вид такой функции. Для оценки возможности применения линейной функции существует несколько способов: приближенных и более точных.
Самым простым способом является визуальная оценка по расположению точек на корреляционном поле, полученном на основании выборки (смотри рисунок 29). На рисунке 29,а точки находятся вблизи воображаемой прямой и поэтому здесь разумно искать линейную функцию регрессии. На рисунке 29,б и 29,в изображены ситуации, в которых линейная функция плохо соответствует действительности.
Более точную оценку линейности связи можно получить с помощью коэффициента линейной корреляции r. Сформулируем свойства этого коэффициента.
1) Если случайные величины X и Y независимы, то теоретически r = 0. Противоположное утверждение неверно и не всегда выполняется.
2) Если в формуле (2.71) поменять местами величины, зависящие от X и Y, то значение r не изменяется, значит,  =
=  .
.
3) если случайные величины X и Y строго линейно зависимы, то есть имеем обычную функцию Y = αX + b, то
r = 
Если значение | r | близко к единице, то надо найти линейную функцию регрессии. Если | r | < 0,5, то обычно уже не стоит использовать линейную функцию. В этом случае можно попробовать найти нелинейную функцию, например, квадратичную функцию (или полиномиальную функцию более высокого порядка)
у =  +
+  (2.76)
(2.76)
коэффициенты которой вычисляют также методом наименьших квадратов, программа их вычисления на ЭВМ несложна. Степенную, экспоненциальную и некоторые другие функции можно линеаризовать путем логарифмирования.
2.4.9 Идея дисперсионного анализа
Случайные величины появляются вследствие воздействия, как правило, множества различных факторов и причин. В дисперсионном анализе исследуется значимость влияния (на результаты испытаний) отдельных факторов, сравнивается их влияние между собой и т. д. С этой целью разделяют дисперсию на части, независимые слагаемые, которые потом сравнивают между собой.
Пусть, например, некоторая величина имеет истинное (генеральное) значение М, в результате её измерения получено значение Х и пусть на процесс измерения влияют случайные независимые факторы А и В. Тогда можно представить отклонение М – Х = α + β + γ, где α – отклонение под влиянием фактора А, β – под влиянием фактора В, а γ – под влиянием остальных, неучтенных факторов, причем α, β и γ независимы.
Найдем дисперсию D (М – Х) = D (α + β + γ). На основании свойств дисперсии (см. п. 1.2.4.2) получаем D Х =  +
+  +
+  , где
, где  характеризует влияние на дисперсию фактора А,
характеризует влияние на дисперсию фактора А,  - влияние фактора В, а
- влияние фактора В, а  - влияние остальных, неучтенных факторов. Дисперсия
- влияние остальных, неучтенных факторов. Дисперсия  называется остаточной дисперсией. Для оценки значимости факторов А или В сравнивают соответствующие дисперсии
называется остаточной дисперсией. Для оценки значимости факторов А или В сравнивают соответствующие дисперсии  или
или  с остаточной дисперсией
с остаточной дисперсией  .
.
Если исследуется влияние одного фактора, то говорят об однофакторном (дисперсионном) анализе, при исследовании влияния двух факторов – о двухфакторном анализе и т. д.
2.4.10 Однофакторный дисперсионный анализ
2.4.10.1 Решение задачи однофакторного анализа
Рассмотрим пример. Пусть в каком - то цехе несколько рабочих выполняют одинаковые операции. Для планирования дальнейшей работы нужно знать, все ли рабочие дают одинаковую по качеству продукцию или нет. Иначе говоря, можно ли игнорировать влияние человеческого фактора на продукцию или нет?
Пусть этот фактор имеет m уровней (в цехе m рабочих). Из каждого уровня (продукции каждого рабочего) сделаем выборку из n элементов. Общее количество выбранных элементов обозначим N = m · n. Вся выборка представляет собой матрицу полученных значений контролируемого показателя х

 значения фактора в выборках
значения фактора в выборках
Полагая, что эта выборка сделана из нормально распределенной генеральной совокупности, и задавая уровень значимости α, нужно проверить основную гипотезу о равенстве средних значений на всех уровнях фактора:  . При альтернативной гипотезе
. При альтернативной гипотезе  не все средние значения
не все средние значения  должны быть равными.
должны быть равными.
В качестве статистики используем величину дисперсионного отношения
F =  , (2.77)
, (2.77)
где 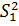 - дисперсия, характеризующая влияние исследуемого фактора
- дисперсия, характеризующая влияние исследуемого фактора  ;
;  – дисперсия, характеризующая влияние остальных факторов (остаточная дисперсия). Если гипотеза
– дисперсия, характеризующая влияние остальных факторов (остаточная дисперсия). Если гипотеза 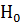 верна, то случайная величина F имеет F – распределение (Фишера) со степенями свободы
верна, то случайная величина F имеет F – распределение (Фишера) со степенями свободы  = m – 1 и
= m – 1 и  = N – m = m (n - 1), соответственно для числителя и знаменателя.
= N – m = m (n - 1), соответственно для числителя и знаменателя.
При проверке гипотезы 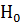 используем правостороннюю критическую область (см. п. 2.3.6), определяемую условием
используем правостороннюю критическую область (см. п. 2.3.6), определяемую условием
Р(F >  ) = α,
) = α,
где  - критическое (табличное) значение (квантиль F - распределения).
- критическое (табличное) значение (квантиль F - распределения).
Если значение статистики [см. формулу (2.77)] входит в критическую область, то гипотезу 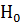 о равенстве средних значений на всех уровнях фактора отвергаем, то есть считаем влияние исследуемого фактора значимым. В противном случае (F <
о равенстве средних значений на всех уровнях фактора отвергаем, то есть считаем влияние исследуемого фактора значимым. В противном случае (F <  ) принимаем гипотезу
) принимаем гипотезу  то есть считаем, что значимость влияния фактора не установлена.
то есть считаем, что значимость влияния фактора не установлена.
Для нахождения величины F найдем сумму квадратов отклонений элементов выборки относительно общего среднего арифметического
Q =  (2.78)
(2.78)
где  =
=  , m – число уровней фактора, n - объём выборки для каждого уровня.
, m – число уровней фактора, n - объём выборки для каждого уровня.
Эту общую сумму можно разделить на два независимых слагаемых (части):
 -
-  ; (2.79)
; (2.79)
 =
=  (2.80)
(2.80)
так, чтобы выполнялось равенство Q = 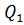 +
+  . Здесь
. Здесь  =
= 
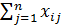 , j = 1, 2, …, m (
, j = 1, 2, …, m (  - групповые средние). Суммой квадратов межгрупповых отклонений, характеризующей влияние (уровня) фактора, является сумма квадратов отклонений групповых средних относительно общей средней (сумма Q 1); Q 2 представляет собой сумму квадратов отклонений значений выборки относительно групповых средних и называется суммой квадратов внутригрупповых отклонений. Эта сумма
- групповые средние). Суммой квадратов межгрупповых отклонений, характеризующей влияние (уровня) фактора, является сумма квадратов отклонений групповых средних относительно общей средней (сумма Q 1); Q 2 представляет собой сумму квадратов отклонений значений выборки относительно групповых средних и называется суммой квадратов внутригрупповых отклонений. Эта сумма  характеризует влияние остальных, неучтённых факторов.
характеризует влияние остальных, неучтённых факторов.
На основании сумм  можно вычислить соответствующие дисперсии:
можно вычислить соответствующие дисперсии:
 =
=  ,
, 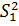 =
= 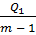 ,
,  =
=  , (2.81)
, (2.81)
где 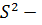 общая дисперсия, ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
общая дисперсия, ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">  дисперсия, характеризующая влияние исследуемого фактора,
дисперсия, характеризующая влияние исследуемого фактора,  остаточная дисперсия.
остаточная дисперсия.
Две последние дисперсии используют при вычислении дисперсионного отношения F (см. формулу 2.77).
При практических вычислениях обычно по выборке находят Q и 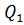 , а
, а  определяют как разность
определяют как разность  и
и 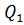 :
:
 = Q -
= Q - 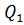 . (2.82)
. (2.82)
2.4.10.2 Решение задачи при одинаковом количестве элементов на всех уровнях
В простейшем случае на каждом уровне фактора выбирают одинаковое количество объектов исследования, то есть одинаковый объём выборок (как в п. 2.4.10.2). Но вычислять суммы по формулам (2.78) – (2.80) достаточно сложно. Более удобные формулы получаем, преобразуя выражения (2.78) и (2.79).
Обозначая N = m · n,  =
=  и
и 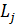 =
=  , окончательно получаем
, окончательно получаем
Q =  -
-  (
(  ; (2.83)
; (2.83)

 . (2.84)
. (2.84)
По исходной матрице (выборке) вычисляем суммы элементов и их квадратов по столбцам ( 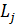 и
и  ).
).
2.4.10.3 Решение задачи при неодинаковом количестве элементов на различных уровнях
На практике не всегда удается гарантировать одинаковое количество элементов на каждом уровне фактора. Обозначим количество элементов на
j–м уровне через 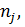 j = 1, 2, …, m. Тогда объём выборки
j = 1, 2, …, m. Тогда объём выборки
N = 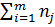 ,
,
формула (2.84) запишется в виде
 =
= 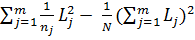 , (2.85)
, (2.85)
а суммы  в виде
в виде  =
= 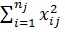 и
и 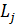 =
=  . Соответственно дисперсии [см. формулу (2.81)] таковы:
. Соответственно дисперсии [см. формулу (2.81)] таковы:
 ,
, 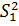 =
= 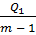 ,
,  =
=  . (2.86)
. (2.86)
Остальные формулы, используемые при решении задач, не изменяются.






