ОСНОВЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Первичная обработка выборок
2.1.1 Генеральная совокупность и выборка
Полная совокупность объектов, или, точнее, совокупность значений какого-то признака объектов, называется генеральной совокупностью. Основной задачей математической статистики является исследование генеральной (полной) совокупности статистически, то есть выяснение (оценка) вероятностных свойств совокупности: распределения, числовых характеристик и т. д.
Однако полное исследование генеральной совокупности обычно практически невозможно или неэкономно. Например, при проверке электролампы одним из её показателей качества считается общее время работы (до сгорания). Аналогичная ситуация имеет место и при проверке качества консервов, снарядов и т. д. Всеобщее исследование (проверку) применяют, как правило, редко. Например, всеобщую перепись населения проводят примерно через 10 лет.
Обычно из генеральной совокупности делают выборку, то есть исследуют только часть её объектов. С помощью выборки оценивают генеральную совокупность по вероятностным свойствам. Чтобы оценки были достоверными, выборка должна быть представительной, то есть её вероятностные свойства должны совпадать или быть близкими к свойствам генеральной совокупности. Для этого надо в достаточном объёме выбирать объекты для исследования случайным образом, то есть гарантировать всем объектам генеральной совокупности одинаковую вероятность подвергнуться исследованию.
Случайно выбранный объект после проверки нужного признака можно возвратить (возвратная или повторная выборка) или не возвратить (безвозвратная или бесповторная выборка) обратно в генеральную совокупность. В первом случае получаем более независимую и представительную выборку.
Часто под генеральной совокупностью понимают и сами исследуемые случайные величины, их значения. Совокупность полученных в испытаниях значений также называется выборкой и обрабатывается статистически. Методы статистической обработки повторной и бесповторной выборок аналогичны.
При исследовании объектов можно фиксировать или измерять значение одного или нескольких признаков (величин). Соответственно говорят об одномерной, двумерной, трехмерной и т. д. выборках. Вначале рассмотрим обработку одномерных выборок.
2.1.2 Вариационный ряд
Выбор объекта из генеральной совокупности и измерение значения признака называется статистическим наблюдением. Результаты наблюдений фиксируют в протоколе или дневнике наблюдений в порядке их появления.
Выборка будет намного наглядней, если все её элементы упорядочить по возрастанию или по убыванию признака. Но в выборке одно значение (варианта) может встречаться несколько раз, и поэтому целесообразно результаты записать в виде таблицы, в первом столбце которой находятся всевозможные значения xi генеральной совокупности (или случайной величины) X, а во втором – числа ni, то есть частоты появления i -го значения. Такую таблицу называют вариационной таблицей или вариационным рядом.
Для составления вариационного ряда нужно:
1) найти минимальное (xmin) и максимальное (xmax) значения в выборке;
2) в первый столбец таблицы записать полученные (различные) значения случайной величины (генеральной совокупности), начиная с xmin и кончая xmax, в порядке их возрастания;
3) подсчитать количество одинаковых значений xi и записать соответствующее им число ni ;
4) подсчитать общее количество элементов в выборке (объём выборки) n и сравнить его с найденным по формуле:
n = 
(2.1)
где m – количество различных значений в вариационном ряде. Если условие (2.1) не выполнено, то повторить все пункты, начиная с третьего.
Пример вариационного ряда по значениям дан в табл. 1 (выборка А).
Если количество вариантов m слишком велико или близко к объёму выборки, то целесообразно составить вариационный ряд по интервалам значений генеральной совокупности, его составляют по выборке из непрерывной генеральной совокупности.
Вариационный ряд по интервалам значений можно получить с помощью приведённого выше алгоритма, где во втором пункте следует:
- заполнить первый столбец таблицы интервалами значений X генеральной совокупности;
- все интервалы выбирать одинаковой длины таким образом, чтобы xmin вошло в первый, а xmax – в последний интервал. Обычно начало интервала входит в интервал, а его конец, – не входит.
В остальных пунктах алгоритма следует слово “значение” заменить словом “интервал”. Пример вариационного ряда по интервалам смотри в таблице 2 (выборка В).
2.1.3 Графики вариационных рядов
Значения генеральной совокупности будут сравнимыми, если использовать относительные частоты (частости) ni / n, их обычно используют при построении графиков. Сумма всех частот должна быть равна единице [см. формулу (2.1)], так как они являются аналогами вероятности:
. (2.2)
Используют два вида графиков выборочного распределения (вариационного ряда): полигон (частот) и гистограмму. Если вариационный ряд составлен по значениям, то полигон строят из отрезков, соединяющих точки, координатами которых являются значения xi и соответствующие относительные частоты ni / n (см. рисунок 17). При построении гистограммы над каждым значением xi строят прямоугольник, высота которого пропорциональна соответствующей относительной частоте ni / n (см. рис.18).
Если вариационный ряд составлен по интервалам, то в качестве значений xi следует рассматривать середины интервалов (см. рисунки 20, 21).
2.1.4 Эмпирическая функция распределения
Каждая генеральная совокупность имеет функцию распределения F (x) [см. формулу (1.19)], которая обычно неизвестна. По выборке можно найти эмпирическую функцию распределения F *(x), где на основании закона больших чисел (теорема Бернулли) вместо вероятностей pi берутся относительные частоты ni / n, так как они при n → 
стабилизируются около значений вероятности pi событий X = xi (это статистическое определение вероятности). Процесс нахождения эмпирической функции распределения F *(x) аналогичен процессу нахождения функции распределения F(x) дискретной случайной величины X [см. п. 1.2.3, формулы (1.20) и (1.21)]:
F *(x) = 
(2.3)
F *(x)= 
(2.4)
Значениями эмпирической функции распределения F *(x) [формула (2.4)] являются так называемые накопленные частоты (смотри таблицы 1 и 2). График эмпирической функции распределения строят так же, как и график функции распределения F (x) дискретной случайной величины (см. рисунок 3).
Если вариационный ряд составлен по интервалам значений и в качестве представителя интервала берётся его середина, то эмпирическая функция составляется так же, как по вариационному ряду по значениям. Таким образом, получаем ломаную линию, являющуюся довольно хорошим приближением графика функции распределения непрерывной случайной величины (сравни рисунки 5 и 22). Такой график является точным, если все значения в каждом интервале распределены равномерно.
2.1.5 Числовые характеристики выборки
2.1.5.1 Среднее арифметическое
Среднее арифметическое 
определяется по формуле:
= 
(2.5)
где xi – элементы выборки, n – её объём. Если объём n выборки и xi не слишком велики, то расчёт “вручную” по этой формуле не вызывает трудности. Для больших выборок необходимо прибегнуть к помощи микрокалькулятора или ЭВМ. Выборочное среднее является оценкой математического ожидания ( или среднего) генеральной совокупности Х.
Если составлен вариационный ряд, в котором могут повторяться одинаковые значения xi, то следует использовать следующую формулу:
где xi – неодинаковые значения (варианты) случайной величины в количестве m, ni – соответствующие им частоты, n – общий объём выборки.
Если вариационный ряд составлен по интервалам значений, то в роли xi в формуле (2.6) используют середины интервалов.
2.1.5.2 Дисперсия выборки
Дисперсию выборки обозначим через 
2. Для вычисления выборочной дисперсии 2 используются формулы:
2 = 
2 , (2.8)
где n – общий объём выборки;
2 = 
2 , (2.9)
где m – количество неодинаковых значений xi, ni – их частоты (повторения).
2.1.5.3 Стандартное отклонение
Выборочное стандартное, или среднеквадратичное, отклонение определяется как квадратный корень из дисперсии:
(2.10)
2.1.5.4 Мода
Если вариационный ряд составлен по значениям генеральной (дискретной) совокупности, то модой выборки является значение, имеющее максимальную частоту. Если вариационный ряд составлен по интервалам значений генеральной совокупности, то мода вычисляется по следующей приближённой формуле:
(2.11)
где x 0 – начало модального интервала, то есть интервала, имеющего максимальную частоту, k – длина модального интервала, ni - частота модального интервала, 
– частоты соответственно предшествующего и последующего за модальным интервалом.
2.1.5.5 Медиана
Медианой выборки является значение серединного элемента вариационного ряда. Если вариационный ряд составлен по значениям генеральной совокупности, то при нечётном объёме выборки n медиана – это действительное значение серединного элемента, а при n чётном - среднее арифметическое двух серединных элементов.
Если вариационный ряд составлен по интервалам значений, то медиана вычисляется по следующей приближённой формуле:
Ме = 
(2.12)
где x 0 – начало медианного интервала, то есть интервала, в котором содержится серединный элемента; k – длина медианного интервала; n – объём выборки; Ti -1 – сумма частот интервалов, предшествующих медианному; ni – частота медианного интервала.
В следующих задачах необходимо для заданных вариационных рядов:
· вычислить относительные и накопленные частоты (частости);
· построить графики вариационного ряда (полигон и гистограмму);
· составить эмпирическую функцию распределения;
· построить график эмпирической функции распределения;
· вычислить числовые характеристики вариационного ряда:
¾ среднее арифметическое ;
¾ дисперсию 
;
¾ стандартное отклонение S,
¾ моду M о;
¾ медиану Ме.
Задача 2.1
Имеется выборка A, её вариационный ряд xi и частоты появления xi (ni) и т. д. (см. таблицу 1).
Таблица 1. Выборка A
| xi | ni | относительные частоты ni / n | Накопленные относительные частоты |
| xmin =0 | 4 | 0,0506 | 0,0506 |
| 1 | 13 | 0,1646 | 0,2152 |
| 2 | 14 | 0,1772 | 0,3924 |
| 3 | 24 | 0,3038 | 0,6962 |
| 4 | 16 | 0,2025 | 0,8987 |
| 5 | 3 | 0,0380 | 0,9367 |
| 6 | 3 | 0,0380 | 0,9747 |
| xmax =7 | 2 | 0,0253 | 1,0000 |
| n =79 | 1,0000 | - |
Все относительные частоты вычисляем с одинаковой точностью. При построении графиков изображаем на оси x значения с 0 по 7 и на оси ni / n – значения с 0 по 0,3038 (рисунки 17 и 18).
Рисунок 17. Полигон вариационного Рисунок 18. Гистограмма ф ряда выборки A вариационного ряда выборки A
Полигон строится для точек xi, а гистограмма – для интервалов, где xi являются их серединами.
Эмпирическую функцию распределения F *(x) находим, используя формулу (2.4) и накопленные частоты, из таблицы 1. Имеем:
F *(x) = 
При построении графика F *(x) откладываем значения функции в интервале от 0 до 1 (рис. 19).
Рисунок 19. График эмпирической функции распределения для выборки A
Вычислим суммы для среднего арифметического и дисперсии по формулам (2.6 и 2.9) и по вариационному ряду (см. таблицу 1).
Далее по формуле (2.6) вычисляем среднее арифметическое
и по формуле (2.9) – дисперсию
2 = 2,3668.
Стандартное (или среднеквадратичное) отклонение 
Вспомним, что 
, 2 и являются выборочными (приближёнными) оценками генеральных (истинных) значений характеристик EX (или 
), DX (или 
) и 
Модой Мо здесь является значение с максимальной частотой, то есть Мо = 3 (см. п. 2.1.5.4). Медиана Ме данного вариационного ряда: Ме = 3 (см. п. 2.1.5.5).
Задача 2.2
Имеется выборка B, её интервалы и частоты ni и т. д. (см. таблицу 2). Рассмотрим вариационный ряд по интервалам значений:
Таблица 2. Выборка B
| Интервалы | ni | относительные частоты ni/n | Накопленные относительные частоты |
| 59-63 | 3 | 0,015 | 0,015 |
| 63-67 | 23 | 0,115 | 0,130 |
| 67-71 | 67 | 0,335 | 0,465 |
| 71-75 | 76 | 0,380 | 0,845 |
| 75-79 | 27 | 0,135 | 0,980 |
| 79-83 | 4 | 0,020 | 1,000 |
|
| n = 200 | 1,000 | - |
При построении графиков вариационного ряда откладываем по оси x значения с 61 по 81 и по оси ni / n – значения с 0.015 по 0,380 (рисунки 20,21).
Рисунок 20. Полигон (частот) вариационного ряда выборки B
Рисунок 21. Гистограмма вариационного ряда выборки B
Далее учитываем, что в качестве представителя каждого интервала взят его конец. Принимая за координаты точек концы интервалов и соответствующие накопленные частоты (см. таблицу 2), соединяя эти точки прямыми линиями, построим график эмпирической функции распределения F (x) - рис.22.
Рисунок 22. График эмпирической функции распределения F (x) выборки B
По формуле (2.6) вычисляем оценку среднего арифметического
а по формуле (2.9) – оценку дисперсии
2 = 14,6176.
Оценка стандартного отклонения = 
Моду находим по формуле (2.11):
Мо = 69 + 4 *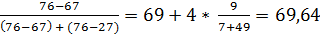 
.
Медиану находим по формуле (2.12):
Ме = 71 + 4 * 
Теория выборочных оценок
2.2.1 Понятие оценки
Генеральные совокупности характеризуются некоторыми постоянными, истинными числовыми характеристиками (распределения). По выборкам можно найти оценки этих характеристик. Вследствие случайности выборок значения оценок одной и той же числовой характеристики, вычисленные по разным выборкам из одной и той же генеральной совокупности, бывают, как правило, различными.
Обозначим неизвестный параметр распределения, то есть числовую характеристику генеральной совокупности X, через q, а оценку этого неизвестного параметра через 
. Оценка – это функция от выборки. Оценки неизвестного параметра можно находить различными способами. Например, если нужно оценить среднее значение q = µ нормального распределения, то можно использовать следующие оценки :
1) 
– единственный элемент выборки. На практике часто так и поступают: измеряют какую-то величину только один раз и этот результат используют как оценку среднего значения;
2) 
- среднее арифметическое максимального и минимального элементов выборки;
3) 
– мода, которая при нормальном распределении равна среднему значению μ;
4) Me – медиана, которая при нормальном распределении также равна среднему значению μ (для малых выборок даёт неплохой результат);
5) 
– среднее арифметическое.
Для того чтобы установить, какая из оценок лучше, надо знать основныесвойства (виды) оценок.
2.2.2 Несмещенные оценки
Несмещенной называется оценка 
среднее значение которой равно оцениваемому параметру θ:
Если это условие не выполняется, то оценку называют смещенной, при этом смещение вычисляется как разность 
Несмещенной оценкой среднего значения μ является среднее арифметическое по выборке.
Аналогично с помощью выборочной дисперсии 2 (см. (2.8)) можно оценить генеральную дисперсию 
Оказывается, что выборочная дисперсия 
является смещённой оценкой дисперсии :
E 
,
то есть смещение (разность) 
что при n → ∞ смещение стремится к нулю. Значит, при достаточно большом объеме выборки n выборочную дисперсию можно приближенно принимать за несмещенную оценку дисперсии . Для оценки дисперсии, несмещенной при малом объеме выборки, используют исправленную дисперсию (с учетом смещения):
, (2.13)
где (n -1)= f называют числом степеней свободы при оценке параметра (здесь одна степень свободы из общего числа n – количества опытов “истрачена” на нахождение по формуле, связи (2.5)).
Если сравнить эту формулу с формулой для выборочной дисперсии из пункта 2.1.5.2 [см. формулы (2.8) – (2.9)], то можно получить аналогичные формулы для вычисления несмещенной оценки 
дисперсии 
; (2.14)
. (2.15)
Задача 2.3
Используя выборку C (таблица 3), вычислить несмещённые оценки среднего значения µ, дисперсии σ2 и стандартного отклонения σ генеральной совокупности: 
Несмещённую оценку среднего значения вычислим по формуле (2.5), несмещённые оценки дисперсии S 2 формуле (2.14) и стандартного отклонения S по формуле S = 
. Вычисления оформляем в таблицу 3.
Таблица 3. Выборка C
| xi | xi -
| (xi - )2
|
| -35 | -5,8 | 33,64 |
| -32 | -2,8 | 7,84 |
| -26 | 3,2 | 10,24 |
| -35 | -5,8 | 33,64 |
| -30 | -0,8 | 0,64 |
| -17 | 12,2 | 148,84 |
| -175 | - | 234,84 |
Имеем:
;
S2 = 
= 46,968;
S = 
2.2.3 Доверительный интервал
Оценки неизвестного параметра θ, рассмотренные выше, называют точечными, так как они определяют одно значение, одну точку на числовой оси. Все точечные оценки параметров распределения генеральной совокупности вычисляют по выборкам, но из-за случайности выборок оценки также являются случайными величинами, отличающимися от постоянного истинного значения параметра θ. Обозначим точность оценки через 
| 
| 
меньше 
(односторонний доверительный интервал или полуинтервал неопределенности), тем точнее оценка.
Любую точность можно получить с определенной вероятностью (надежностью) γ:
P (| |≤ ∆)= γ (2.16)
Если преобразовать это выражение, то можно переписать
P ( 
≤ ∆)= γ
или
P ( 
≤ 
≤ 
∆)= γ (2.17)
Условие (2.17) означает, что интервал | , ∆| покрывает (т.е. включает в себя) значение генерального параметра 
с заданной доверительной вероятностью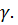 
Точность оценки фактически определяет длину доверительного (двухстороннего, симметричного) интервала (2 
Доверительная вероятность 
задается обычно значением, близким к единице, например, 0,90; 0,95; 0,98; 0,99 и т. д. Дополнительная (до 1) к ней величина α =1-γ называется уровнем значимости.
Доверительная вероятность γ, точность оценки ∆ и объем выборки n связаны между собой. Если определены две величины из них, то тем самым будет определена и третья.
2.2.4 Доверительный интервал для среднего значения μ нормального распределения при известном σ
Пусть задана генеральная совокупность с нормальным распределением X ∈ N (μ, σ ), для которой генеральное значение стандартного отклонения σ известно. Для оценки параметра μ воспользуемся величиной . Заметим, что и среднее арифметическое , и элементы выборки 
, 
из-за случайности выборок являются случайными величинами. Все элементы выборки имеют то же распределение, что и генеральная совокупность: 
∈ N (μ, σ), i = 1, 2, …, n. Среднее арифметическое также имеет нормальное распределение:
∈ N (μ,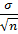 
).
По формуле (2.16) получим
P (| 
. (2.18)
C другой стороны, заменяя в (1.45) X на , σ на σ/ 
и ε на ∆ (допустимая точность оценки, допустимая погрешность), получим:
P (| 
) – 1 = 2Ф( 
) – 1 = γ, (2.19)
где 
= . Отсюда находим полуширину симметричного доверительного интервала
∆ = 
. (2.20)
Используя соотношения (2.17) и (2.18), можно записать формулу для вычисления доверительного интервала:
P ( 
где выражение в скобках определяет полный доверительный интервал (2 ∆).
Вычислим значение переменной . На основании формулы (2.19) получим условие
Ф( 
Согласно этому условию, из таблиц (см. приложение 3) найдем значение аргумента (его называют квантилем нормального распределения).
2.2.5 Доверительный интервал для среднего значения μ нормального распределения при неизвестном σ
Пусть задана генеральная совокупность с нормальным распределением X ∈ N (μ, σ), где значение стандартного отклонения σ неизвестно, то есть непосредственно воспользоваться нормальным распределением N (μ, σ) нельзя. Однако известно, что случайная величина
t = 
где S – несмещенная оценка стандартного отклонения (см. 2.14) генеральной совокупности, n – объем выборки, имеет распределение Стьюдента (t -распределение) с числом степеней свободы f = n – 1.
Для получения интервальной оценки – доверительного интервала потребуем, чтобы выполнялось условие
P (| 
где 
= t, а 
– доверительная вероятность.
Величина 
– квантиль (иначе - процентная точка) определяется по таблицам t -распределения Стьюдента (см. приложение 5). Соответственно для противоположного события t > нужно использовать условие
P (| 
где 
уровень значимости, обычно доверительная вероятность γ ≫ α, например, 0,95≫0,05.
Число степеней свободы для t -распределения равно f = n – 1.
Преобразуя условие (2.24), имеем
P ( 
) = γ, (2.25)
где двухсторонний доверительный интервал указан в скобках. Полученная формула аналогична формуле (2.20). Здесь допустимая точность (вернее допустимая погрешность)
∆ = . (2.26)
2.2.6 Доверительный интервал для дисперсии 
нормального распределения
Предположим, что генеральная совокупность имеет нормальное распределение X ∈ N (μ, σ). Тогда случайная величина
(2.27)
имеет 
– распределение (распределение Пирсона) с числом степеней свободы f = n - 1. Случайная величина с 
распределением принимает только неотрицательные значения. По таблицам 
-распределения (см. приложение 4) можно найти квантиль χα 2, удовлетворяющий следующему условию: P (χ2>χα 2) = α = 1- γ, где α – уровень значимости (см. п.2.3 и рис. 23).
По таблицам 
распределения всегда можно найти такие два числа 
, которые удовлетворяли бы условию
P ( 
. (2.28)
Таких пар чисел (границ) существует бесконечное множество. Чтобы зафиксировать одну такую пару 
, введем дополнительное условие (симметричность по вероятности) (рисунок 24):
P ( 
. (2.29)
Рисунок 23. Использование таблицы Рисунок 24. Нахождение чисел
распределения
Из таблиц (приложение 4), используя условие (2.29), получаем 
. Для нахождения 
используем вероятность противоположного события
P ( 
. (2.30)
Заменяя в формуле (2.28) его значением из формулы (2.27) и выполняя преобразования, получаем
) = γ, (2.31)
где в скобках задан доверительный интервал для дисперсии .
Извлекая квадратный корень из обеих сторон неравенства, определяющего доверительный интервал для дисперсии , получаем доверительный интервал для среднего квадратичного (стандартного) отклонения σ:
≤ σ ≤ 
. (2.32)
Задача 2.4
Найти доверительные интервалы для среднего значения µ, дисперсии σ2 и стандартного отклонения σ генеральных совокупностей при доверительной вероятности γ = 0,95, если из генеральной совокупности сделана выборка C (таблица 3 из задачи 2.3).
С доверительной вероятностью γ = 0, 95 по формуле (2.25) найдём доверительные интервалы для среднего значения (2.25), дисперсии σ2 по формуле (2.31) и стандартного отклонения σ по формуле (2.32), используя выборку C (n =6).
Из таблицы распределения Стьюдента (приложение 5) найдём квантиль = 2,571 (при f = 6-1 = 5; 
, а из таблицы
– распределения (приложение 4):
u 1 = 0, 831 и u 2 = 12,83, p = 
.
Найдем доверительные интервалы, при = -29,2; S 2 = 46,968; S = 6,85; n =6 (см. задачу 2.3):
-по формуле (2.26) получаем ∆ = 2,571 * 
, затем интервалы:
-для математического ожидания µ: (-29,2 - 7,19) ≤ µ ≤ (-29,2 + 7,19), то есть -36,39 ≤ µ ≤ -22,01;
-для дисперсии: при 
= 
,
а доверительный интервал для с.к.о σ:
18,30 
2.2.7 Определение необходимого объема выборки n
До сих пор мы рассматривали обработку готовых выборок с фиксированным объемом n. Часто стоит вопрос: какой объем должна иметь выборка, чтобы можно было получить результаты нужной точности? По закону больших чисел предпочтение отдается выборкам с большим объемом. Но обычно большой объем выборки требует и больших затрат для ее получения (и обработки). Поэтому на практике целесообразно использовать тот минимально необходимый объем, который позволяет получить удовлетворительные результаты по точности оценок при заданном уровне доверия γ.
Для вычисления доверительных интервалов среднего значения нормального распределения, можно, используя формулу (2.20), оценить необходимый объем выборки
n = 
Таким образом, объем выборки n прямо пропорционален (известной) дисперсии и квадрату квантиля нормального распределения 
(он зависит от γ) и обратно пропорционален квадрату допустимой погрешности 
Если мы хотим получить интервал с большей доверительной вероятностью γ (вместе с этим увеличивается и 
то следует увеличить объем выборки n. Если мы хотим сузить доверительный интервал, то есть интервал неопределенности оценки, то должны увеличить объем выборки n. Итак, с помощью формулы (2.33) вычисляется необходимый объем выборки при известном σ.
Однако, обычно значение σ неизвестно и тогда оценку для необходимого объема n выборки получаем из формулы (2.26):
n = 
По формуле (2.33), задавая σ, можно оценить соответствующий объем выборки n до получения самой выборки. По формуле (2.34) можно определить нужный объем выборки n после обработки результатов уже имеющейся пробной, небольшой серии опытов, по которой вычисляется несмещенная оценка дисперсии генеральной совокупности .
Целесообразно, используя последовательно формулы (2.33) и (2.34) при заданном γ, находить уточненное значение объема выборки n, необходимого для получения требуемой точности (погрешности) оценки ∆.
Задача 2.5
Считая выборку C, заданную в задаче 2.3, пробной, определить минимальный объём выборки (количество необходимых опытов) n для нахождения доверительного интервала среднего значения µ при допустимой точности ∆ = 3 и доверительной вероятности γ = 0,99.
Для оценки минимального объёма планируемой основной выборки воспользуемся формулой (2.34) и пробной выборкой С.
При = 0,99, ∆ = 3 и n = 6 имеем: f = n -1 = 6 – 1 = 5; S = 6, 85;
t 0,99 = 4,03 (двусторонняя критическая область).
Предварительно минимально необходимый объём выборки равен
n = 
(опытов, измерений), тогда
f = n -1 = 85-1= 84, а t 0,99 = 2,64.
Уточнение значения необходимого объёма выборки:
n ′ = (2,64∙6.85/3)² = 36,33 ≈ 37, при этом n ′ t 0,99 = 2,72 и
n ″=( 2,72∙6.85/3)² = 38,57 ≈ 39 опытов.
Статистические гипотезы
2.3.1 Понятие статистической гипотезы
Статистической гипотезой называется любое утверждение о виде или свойствах распределения, наблюдаемых в эксперименте случайных величин. Например, случайная величина Х имеет распределение Пуассона, случайная величина с нормальным распределением имеет среднее значение μ = 5 или μ ≠ 5 и т.д. Статистические гипотезы проверяются статическими методами, с помощью статистических критериев.
Гипотезы о неизвестном параметре θ распределения бывают простые и сложные; простая гипотеза утверждает, что параметр θ имеет одно конкретное значение ( например, θ = 
сложнаягипотеза утверждает, что параметр θ имеет значение из совокупности (интервала) значений (например, θ< 
.
Основную (проверяемую) гипотезу обозначим 
Обычно вырабатывают еще и альтернативную гипотезу 
, отрицающую или исключающую основную гипотезу Таким образом, в результате проверки можно принимать только одну из гипотез 
или , отвергая в это же время другую.
Гипотезу проверяют на основании выборки, полученной из генеральной совокупности. Из-за случайности и малого объема выборки в результате проверки могут возникать ошибки и приниматься неправильные решения. В принципе возможны два рода ошибок. Ошибка первого рода имеет место тогда, когда отвергается, будучи правильной, гипотеза 
, а принимается неверная гипотеза . При ошибке второго рода принимается неправильная гипотеза 
, хотя верна альтернативная .
Таким образом, по одним выборкам принимается правильное решение, а по другим – неправильное. Решение принимается по искомому значению некоторой характеристики (функции) выборки, называемой статистикой или статистической характеристикой (это может быть, например, среднее значение). Множество значений этой статистики можно разделить на два непересекающихся подмножества:
¾ значения статистики, при которых гипотеза Н0 принимается (не отклоняется), называемые областью принятия гипо тезы (допустимой областью), например, доверительный интервал;
¾ значения статистики, при которых гипотеза Н0 отвергается (отклоняется) и принимается гипотеза Н 1, называемая критической областью (см. рис. 25), ей соответствуетвероятность, равная 𝛼.
Очевидно, что проверка гипотез выполняется при малой вероятности принятия неправильных решений. Допустимая вероятность ошибки первого рода обозначается через a и называется уровнем значимости 𝛼 = 1 - 𝛾. Значение 𝛼 обычно мало (0,1, …, 0,001). Но уменьшение вероятности ошибки первого рода обычно вызывает увеличение вероятности ошибки второго рода(b).
Статистика выбирается так, чтобы вероятности α и β были бы минимальными (методы выбора наилучшей статистики здесь не рассматриваются). Будем предполагать, что распределение статистики при правильной гипотезе Н0известно.
Чтобы определить критическую область для статистики, используют уровень значимости α и учитывают вид альтернативной гипотезы Н1. Основная или нуль-гипотеза Н0 о значении неизвестного параметра q распределения обычно выглядит так:
Н0: q = q 0.
Альтернативная гипотеза Н1 может при этом иметь один из следующих видов:
Н1: q < q 0, Н1: q > q 0 или Н1: q ¹ q 0.
Соответственно этому можно получить левостороннюю, правостороннюю или двустороннюю критические области (рисунок 25). Граничные точки критических областей определяют по таблицам распределения статистики (считаем распределение известным), используя значения (квантили), отвечающие уровню доверительной вероятности γ (или уровню значимости α = 1- γ).
Проверка статистической гипотезы состоит из следующих эта пов:
1) определение (выбор) гипотез Н0 и Н1;
2) выбор статистической характеристики (статистики) и задание уровня значимости α;
3) определение границ критической области (по таблицам, по уровню значимости α и по альтернативной гипотезе Н1);
4) вычисление по выборке значения статистики (искомой статистической характеристики);
5) сравнение значения статистики с границей критической области;
6) принятие решения (гипотезы): если значение статистики не попадает в критическую область ( см. рис. 25 ), то принимается нуль-гипотеза Н0 и отвергается альтернативная гипотеза H 1 (здесь возможна ошибка второго рода), а если попадает в критическую область, то отвергается гипотеза Н0 и принимается гипотеза Н1 (в этом случае возможна ошибка первого рода).
допустимые области
α α α/2 α/2
k k k1 k2
| б) |
| в) |
| а) |
Рисунок 25. Критические области:
а – левосторонняя, б – правосторонняя, в – двусторонняя
Иногда целесообразно перед определением альтернативной гипотезы H 1 выполнить этап 4, где для получения значения статистики нужно вычислить несмещённые оценки параметров генеральной совокупности. Например, если проверяется нуль-гипотеза Н0: 𝜇 ≠ 5 и несмещенная оценка среднего значения = 7,2, т.е. > 𝜇, то имеют смысл только следующие альтернативные гипотезы Н1: 𝜇 > 5 или Н1: 𝜇 = 5.
Результаты проверки статистической гипотезы нужно интерпретировать так: если мы приняли альтернативную гипотезу Н1, то можно считать ее доказанной, а если приняли основную гипотезу Н0, то мы признали лишь, что гипотеза Н0 при заданном уровне значимости α не противоречит результатам наблюдений. Однако этим свойством наряду с Н0 могут обладать и другие гипотезы. Например, если мы принимаем гипотезу Н0: 𝜇 = 5, то может случиться, что по данной выборке можно, при заданном α, принять и другие гипотезы, например, Н0: 𝜇 = 5,5 или Н0:
𝜇 = 4 и т.д. Вопрос о том, как найти среди них наилучшую гипотезу, здесь не рассматриваем. Следует помнить, что, принимая гипотезу Н0, для надежности надо проводить еще дополнительные (дальнейшие) исследования.
2.3.2 Гипотеза о среднем значении нормального распределения при известном σ
Предполагаем, что генеральная совокупность имеет нормальное распределение X ∈ N (μ, σ), причём значение σ известно. При уровне значимости a нужно проверить нуль-гипотезу Н0: 
( например, µ0 = 5). В качестве альтернативной можно использовать одну из следующих гипотез Н1: 
, Н1: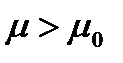 
или Н1: 
. В качестве статистики (статистической характеристики) воспользуемся нормированной (безразмерной) случайной величиной
, (2.35)
где 
- неизвестное генеральное среднее значение,
которая при истинной гипотезе Н0 имеет нормированное нормальное распределение Z ∈ N (0, 1) (см. п. 1.2.8, формулы 1.43 … 1.44).
Критическую область определяем с помощью таблицы функции распределения (см. приложение 3) Ф(х) нормального распределения ( x >0).
Если альтернативная гипотеза имеет вид Н1: 
, то используем левостороннюю критическую область, которая удовлетворяет (рисунок 26) следующему условию:
P (Z < - 
(2.36)
где аргумент 
- квантиль нормированного N -распределения (из приложения 3 для х = z). Вспомним, что 
- это вероятность попадания значения статистической характеристики (здесь z) в критическую область.
Таблицы составлены только для положительных значений аргумента (Z >0), поэтому из таблицы найдем , учитывая [см. формулу (1.17)], что
Ф( ) = 1 – . (2.37)
Отсюда следует, что критическая область (здесь - левосторонняя) – это множество таких Z, для которых
Z <- 
(2.38)
f (z) f (z)
- 
0 z 0
