Тесты по м атематике
| № | Вопрос | № правильного ответа | ||||||||
| Тема 1. Производная функции | ||||||||||
| 1.1 | Производная функции 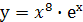 имеет вид:
а) имеет вид:
а)  б)
б)  в)
в)  г)
г) 
| |||||||||
| 1.2 | Производная функции 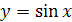 в точке в точке  равна:
а) -1
б) 1
в) равна:
а) -1
б) 1
в)  г)
г) 
| |||||||||
| 1.3 | Производная функции  имеет вид:
а) имеет вид:
а) 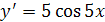 б)
б)  в)
в)  г)
г) 
| |||||||||
| 1.4 | Дифференциал функции  имеет вид:
а) имеет вид:
а)  б)
б)  в)
в)  г)
г) 
| |||||||||
| 1.5 | Дана функция  . Установите соответствие между производными функции в соответствующих точках и их значениями. . Установите соответствие между производными функции в соответствующих точках и их значениями.
а) 1- n, 2- m, 3- k; б) 1- m, 2- n, 3- k; в) 1- k, 2- m, 3- n; | |||||||||
| 1.6 | Производная функции 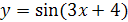 имеет вид:
а) имеет вид:
а)  б)
б) 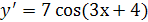 в)
в)  г)
г) 
| |||||||||
| 1.7 | Найдите производную функции  а) 2
б) 4х2
в) 12х
г) 12х2
а) 2
б) 4х2
в) 12х
г) 12х2
| |||||||||
| 1.8 | Найдите производную функции 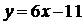 .
а) 6
б) -5
в) 11
г) 6х .
а) 6
б) -5
в) 11
г) 6х
| |||||||||
| 1.9 | Найдите производную функции  .
а) 1
б) .
а) 1
б)  в)
в)  г)
г) 
| |||||||||
| 1.10 | Вычислите значение производной функции  в точке хо=2.
а) 12
б) 0
в) 11
г) 6 в точке хо=2.
а) 12
б) 0
в) 11
г) 6
| |||||||||
| 1.11 | Найдите производную функции  .
а) .
а)  б)
б)  в)
в) 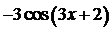 г) 6х
г) 6х
| |||||||||
| 1.12 | Найдите производную функции  .
а) -5
б) 0
в) 7
г) 12 .
а) -5
б) 0
в) 7
г) 12
| |||||||||
| 1.13 | Задана функция
 .
Найти производную функции
а) .
Найти производную функции
а) 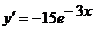 б)
б)  в)
в) 
| |||||||||
| 1.14 | Найти дифференциал функции 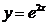 а)
а) 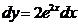 б)
б)  в)
в) 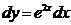
| |||||||||
| Тема 2. Интеграл функции | ||||||||||
| 2.1 | Укажите функцию, для которой
F(х) = 17х2 - 7cosx
является первообразной.
а) у = 17x+7sinx
б) у = 5  х3-7sinx
в) у = 7cosx
г) y = 34x+7sinx х3-7sinx
в) у = 7cosx
г) y = 34x+7sinx
| |||||||||
| 2.2 | Укажите первообразную функции y=5x а) 2,5x2 б) 1 в) 5 г) 9+5x2 | |||||||||
| 2.3 | Определенный интеграл – это… а) формула.; б) совокупность первообразных функций; в) первообразная функция; г) число | |||||||||
| 2.4 | Найдите неопределенный интеграл  а)
а) 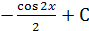 б) 2
в)
б) 2
в)  г)
г) 
| |||||||||
| 2.5 | 
 а) 3
б) 0
в) 6x
г) 2
а) 3
б) 0
в) 6x
г) 2
| |||||||||
| 2.6 | Найдите неопределенный интеграл
 а)
а)  б)
б) 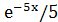 в)
в) 
| |||||||||
| 2.7 | Найдите неопределенный интеграл
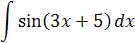 а)
а)  б)
б)  в)
в) 
| |||||||||
| 2.8 | Найдите неопределенный интеграл
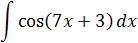 a)
a)  б)
б)  в) 7
в) 7 
| |||||||||
| Тема 3. Дифференциальные уравнения | ||||||||||
| 3.1 | Чем определяется порядок дифференциального уравнения? а) высшим порядком входящей в него производной б) порядком наименьшей входящей в него производной в) степенью функции | |||||||||
| 3.2 | Какое количество произвольных постоянных содержит частное решение дифференциального уравнения первого порядка? а) не содержит вообще б) 1 в) 2 | |||||||||
| 3.3 | Какое количество произвольных постоянных содержит общее решение дифференциального уравнения первого порядка? а) 1 б) 2 в) 0 | |||||||||
| 3.4 | Укажите общее решение дифференциального уравнения
 а)
а)  б)
б) 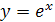 в)
в) 
| |||||||||
| 3.5 | Найти решение дифференциального уравнения
 k =const
а)
k =const
а)  б)
б)  в)
в) 
| |||||||||
| 3.6 | Общим решением дифференциального уравнения является: а) функция, при подстановке которой в исходное уравнение оно обращается в тождество б) производная функции, входящей в это уравнение; в) значение аргумента; г) порядок уравнения | |||||||||
| 3.7 | Частным решением дифференциального уравнения является: а) функция, не содержащая произвольных постоянных и при подстановке обращающая уравнение в тождество б) конкретное значение аргумента; в) конкретное значение функции; г) корень характеристического уравнения | |||||||||
| 3.8 | Дифференциальное уравнение  в результате разделения переменных сводится к уравнению:
а) в результате разделения переменных сводится к уравнению:
а)  ;
б) ;
б)  ;
в) ;
в) 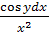 =dy;
г) =dy;
г) 
| |||||||||
| 3.9 | Укажите частное решение дифференциального уравнения
 , , 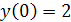 а)
а) 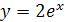 б)
б) 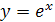 в)
в) 
| |||||||||
| 3.10 | Дифференциальное уравнение  в результате разделения переменных сводится к уравнению:
а) в результате разделения переменных сводится к уравнению:
а)  ;
б) ;
б)  ;
в) ;
в)  =dy;
г) =dy;
г) 
| |||||||||
| Тема 4. Теория вероятности. Математическая статистка | ||||||||||
| 4.1 | Теория вероятности – это…. а) раздел математики, изучающий связи между вероятностями случайных событий; б) раздел математики, изучающий связи между экспериментальными данными; в) раздел математики, изучающий связи между разделами систематизации; г) раздел математики, изучающий связи между функциями. | |||||||||
| 4.2 | В урне 4 черных и 6 белых шаров. Из урны случайным образом берут один шар. Вероятность того, что этот шар окажется черным, равна: а) 0.4 б) 0.2 в) 0.6 г) 1 | |||||||||
| 4.3 | Закон распределения дискретной случайно величины Х имеет вид:
Вероятность а) 0.3 б) 0.7 в) 0 г) 0.5 | |||||||||
| 4.4 | Математическое ожидание дискретной случайной величины, заданной законом распределения, равно
а) 5.9 б) 15 в) 5 г) 1 | |||||||||
| 4.5 | По цели произведено 10 выстрелов, зарегистрировано 7 попаданий, тогда относительная частота попадания в цель равна: а) 0.7 б) 0.5 в) 0.35 г) 0.3 | |||||||||
| 4.6 | Вероятность появления одного из двух несовместных событий А и В, вероятности которых соответственно Р(А)=0.4 и Р(В)=0.3, равна: а) 0.7 б) 0.1 в) 0.12 г) 0.3 | |||||||||
| 4.7 | Если вероятность попадания в мишень составляет 0.3, тогда вероятность промаха равна: а) 0.7 б) 0.5 в) 1.2 г) 0.3 | |||||||||
| 4.8 | Если вероятность попадания в мишень первым стрелком равна 0.4, вторым – 0.5, тогда вероятность поражения цели обоими стрелками равна: а) 0.2 б) 0.45 в) 0.9 г) 0.3 | |||||||||
| 4.9 | Дисперсия случайной величины, заданной законом распределения, равна
а) 0.76 б) 1.4 в) 0.8 г) 2.04 | |||||||||
| 4.10 | В урне 3 желтых и 7 синих шаров. Из урны случайным образом берут один шар. Вероятность того, что этот шар окажется желтым равна: а) 0.3 б) 0.2 в) 0.5 г) 1 | |||||||||
| 4.11 | При увеличении математического ожидания μ нормально распределенной случайной величины абсцисса максимума кривой Гаусса: а) смещается вправо – в область положительных значений; б) смещается влево – в область отрицательных значений; в) остается неизменной; г) результат зависит от конкретного значения μ. | |||||||||
| 4.12 | При увеличении σ нормально распределенной случайной величины абсцисса максимума кривой Гаусса: а) не меняет своего значения; б) смещается влево– в область отрицательных значений; в) смещается вправо– в область положительных значений; г) результат зависит от конкретного значения σ. | |||||||||
| 4.13 | Полигоном частот называется: а) графическое изображение дискретного статистического ряда распределения; б) графическое изображение интервального ряда распределения; в) график функции; г) графическое изображение отношения частоты и относительной частоты. | |||||||||
| 4.14 | Гистограммой частоты называется: | |||||||||
| а) графическое изображение интервального ряда распределения; б) графическое изображение дискретного ряда распределения; в) график функции; г) графическое изображение отношения частоты и относительной частоты. | ||||||||||
| 4.15 | Математическая статистика -- это: а) раздел математики, посвященный математическим методам систематизации, обработки и использования статистических данных для научных и практических выводов; б) раздел математики, изучающий связи между экспериментальными данными; в) раздел математики, изучающий связи между методами систематизации; г) раздел математики, изучающий связи между функциями. | |||||||||
| 4.16 | Выборкой называется: а) множество объектов, случайно отобранных из генеральной совокупности; б) множество объектов, однородных относительно нескольких признаков; в) множество объектов, однородных относительно одного признака; г) множество объектов, собранных по одному признаку. |