Решение задач С2 из методом координат.
Люди делятся по своим наклонностям на два
типа: одним больше нравятся выкладки, другим -
- наглядность.
Прасолов В.В., Тихомиров В.М.
Из предисловия к книге «Геометрия»
Применение координатного метода в стереометрии чаще всего встречается в задачах на нахождение угла между двумя прямыми. Между тем возможности его намного шире. В отношении школьного курса геометрии можно сказать, что в некоторых случаях метод координат дает возможность строить доказательства и решать многие задачи более рационально, красиво, чем чисто геометрический способ. Этим методом легко решаются задачи на нахождение угла между прямой и плоскостью, угла между двумя плоскостями, расстояния от прямой до плоскости, расстояния между скрещивающимися прямыми.
Как показывает практика, этот метод доступен учащимся даже с недостаточно развитым пространственным воображением, что позволяет повысить уровень их подготовки к ЕГЭ.
Что же требуется, чтобы освоить пространственный метод координат?
Во – первых, знание определенных формул; во – вторых, умение вычислять координаты вершин многогранников и точек, расположенных на их ребрах и гранях.
Формулы и методы решения.
Угол между прямыми.
Вектор 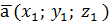 лежит на прямой а, вектор
лежит на прямой а, вектор  лежит на прямой b. Косинус угла
лежит на прямой b. Косинус угла  между прямыми a и b определяется по формул
между прямыми a и b определяется по формул
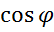
 (1)
(1)
( 0, так как угол
0, так как угол 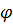 - острый).
- острый).
Угол между прямой и плоскостью.
Прямая Ɩ образует с плоскостью α угол  (
(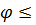 90˚). Вектор
90˚). Вектор 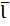 (
( ) – направляющий вектор прямой Ɩ.
) – направляющий вектор прямой Ɩ.
Плоскость α задана уравнением
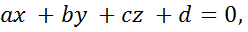
и  - вектор нормали. Синус угла
- вектор нормали. Синус угла  определяется по формуле
определяется по формуле
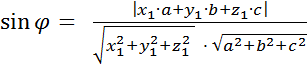 . (2)
. (2)
Угол между двумя плоскостями.
Плоскость α задана уравнением 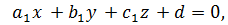
и ее вектор нормали 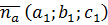 ; плоскость
; плоскость 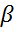 задана уравнением
задана уравнением  ее вектор нормали
ее вектор нормали 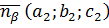 . Для угла
. Для угла 
между плоскостями α и 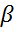 справедлива формула
справедлива формула
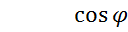
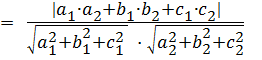 (3)
(3)
( 0, так как угол
0, так как угол 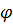 - острый).
- острый).
Расстояние от точки до плоскости.
Расстояние h от точки  до плоскости α, заданной уравнением
до плоскости α, заданной уравнением 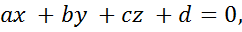 определяется по формуле
определяется по формуле
 . (4)
. (4)
Расстояние между двумя точками.
Расстояние d между двумя точками,  , равно
, равно
 . (5)
. (5)
Координаты вершин многогранников.
Определим координаты вершин некоторых многогранников.
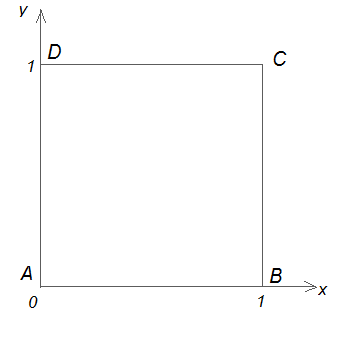
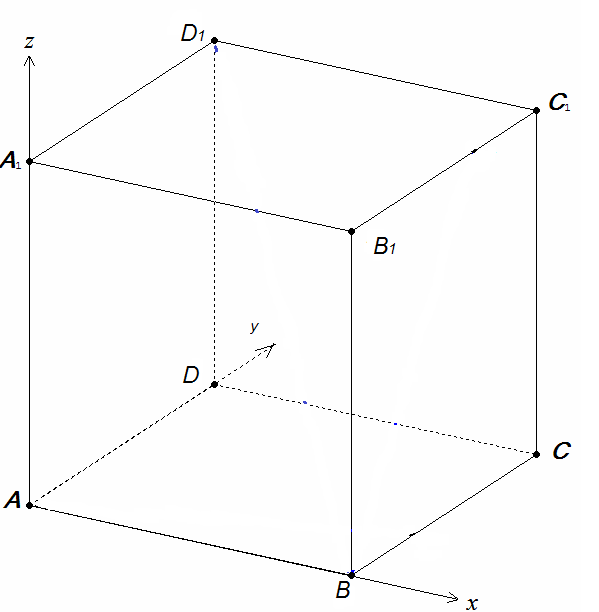
1. Единичный куб А…D 1 .
Начало координат – в точке А; прямая АВ – ось x, прямая АD – ось y, прямая АА1 – ось z. Тогда вершины куба имеют координаты: А (0;0;0), В (1;0;0), С (1;1;0), D (0;1;0), А1 (0;0;1), В1 (1;0;1), С1 (1;1;1), D1 (0;1;1).
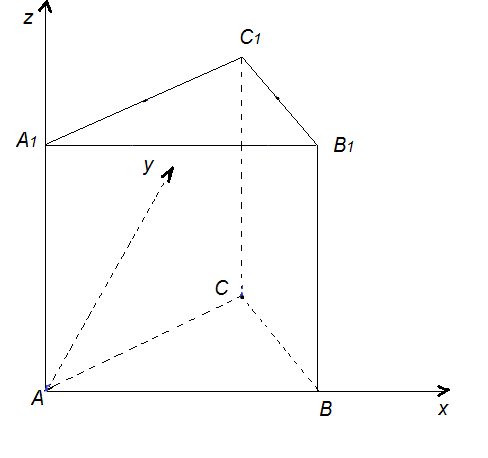
2. Правильная треугольная призма АВСA1B1C1, все ребра которой равны 1.
Начало координат – в точке А; прямая АВ – ось x; прямая, проходящая через точку А в плоскости АВС перпендикулярно прямой АВ, - ось y; прямая АА1 – ось z. Тогда вершины призмы имеют координаты: А (0;0;0), В (1;0;0), С (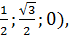 А1 (0;0;1), В1 (1;0;1), С1 (
А1 (0;0;1), В1 (1;0;1), С1 (

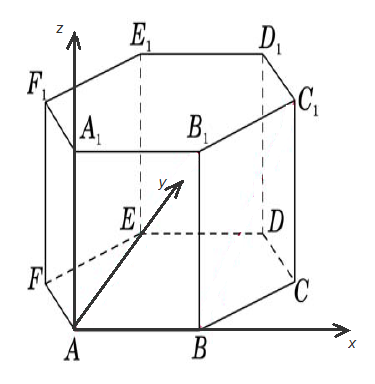
3. Правильная шестиугольная призма А…F1, все ребра которой равны 1.
Начало координат – в точке А; прямая АВ – ось х; прямая, проходящая через точку А в плоскости АВС перпендикулярно прямой АВ, - ось у; прямая АА1 – ось z. Тогда вершины призмы имеют координаты:А(0;0;0), В(1;0;0), С ( D (1;
D (1; 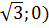 , Е (0;
, Е (0; 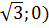 , F (
, F ( ;
; 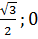 ), А1 (0;0;1), В1 (1;0;1), С1 (
), А1 (0;0;1), В1 (1;0;1), С1 (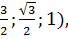 D 1 (1;
D 1 (1; 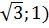 , Е1 (0;
, Е1 (0; 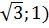 , F1 (
, F1 ( ;
; 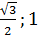 ).
).
На выносном чертеже основания АD = BE = CF = 2R = 2; R – радиус окружности, описанной вокруг правильного шестиугольника; R = 1; АЕ = 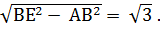

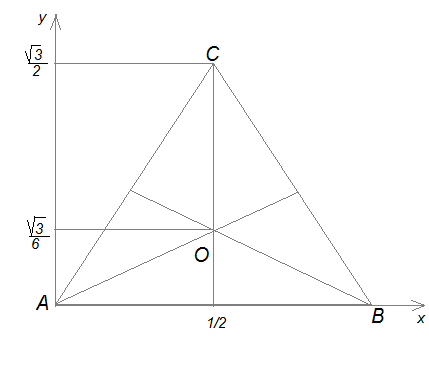
4. Правильная треугольная пирамида (тетраэдр) ABCD, все ребра которой равны 1.
Начало координат – в точке А; прямая АВ – ось х; прямая, проходящая через точку А в плоскости АВС перпендикулярно прямой АВ, - ось у; прямая, проходящая через точку А перпендикулярно плоскости АВС, - ось z. Тогда вершины тетраэдра имеют координаты: А (0;0;0), В (1;0;0), С (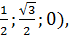 D (
D ( . Точка D проектируется в точку О – точку пересечения медиан треугольника АВС, которая делит медианы в отношении 2:1, считая от вершин треугольника. Высота тетраэдра DO выражается из прямоугольного треугольника АОD: DA = 1, AO =
. Точка D проектируется в точку О – точку пересечения медиан треугольника АВС, которая делит медианы в отношении 2:1, считая от вершин треугольника. Высота тетраэдра DO выражается из прямоугольного треугольника АОD: DA = 1, AO = 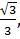 DO =
DO = 

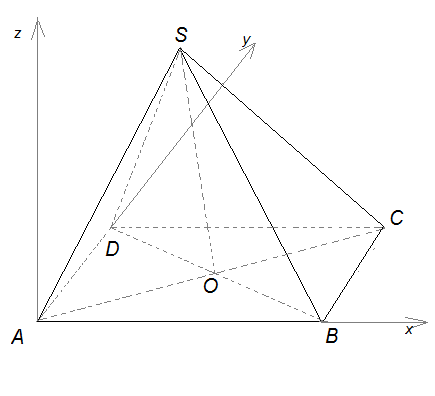
5. Правильная четырехугольная пирамида SA BCD, все ребра которой равны 1.
Начало координат – в точке А; прямая АВ – ось х; прямая АD – ось у; прямая, проходящая через точку А перпендикулярно плоскости АВС, - ось z. Тогда вершины пирамиды имеют координаты: А (0;0;0), В (1;0;0), С (1;1;0), D (0;1;0), S ( Точка S проектируется на плоскость АВС в точку пересечения диагоналей квадрата АВС D – точку О. Высота пирамиды SO выражается из прямоугольного треугольника АОS: SO =
Точка S проектируется на плоскость АВС в точку пересечения диагоналей квадрата АВС D – точку О. Высота пирамиды SO выражается из прямоугольного треугольника АОS: SO = 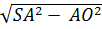 , SA = 1, AO =
, SA = 1, AO = 
SO = 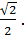

6. Правильная шестиугольная пирамида SABCDEF, стороны которой равны 1, а боковые ребра равны 2.
Начало координат в точке А; прямая АВ – ось х; прямая, проходящая через точку А в плоскости АВС перпендикулярно прямой АВ, - ось у; прямая, проходящая через точку А перпендикулярно плоскости АВС, - ось z. Тогда вершины пирамиды имеют координаты: А (0;0;0), В (1;0;0), С (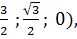 D (1;
D (1;  0), Е (0;
0), Е (0; 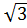 ; 0), F (
; 0), F ( ;
;  Точка S проектируется на плоскость АВС в точку О – точку пересечения диагоналей шестиугольника АВСDEF. Высота пирамиды SO выражается из прямоугольного треугольника АОS:
Точка S проектируется на плоскость АВС в точку О – точку пересечения диагоналей шестиугольника АВСDEF. Высота пирамиды SO выражается из прямоугольного треугольника АОS:
SO = 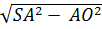 , SA = 2, AO = 1, SO =
, SA = 2, AO = 1, SO = 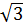 .
.


Примеры решения задач.
Угол между прямыми.
1. В единичном кубе ABCDA1B 1 C 1 D1 найдите угол между прямыми A1D и D1E, где Е – середина ребра CC1.
Решение.
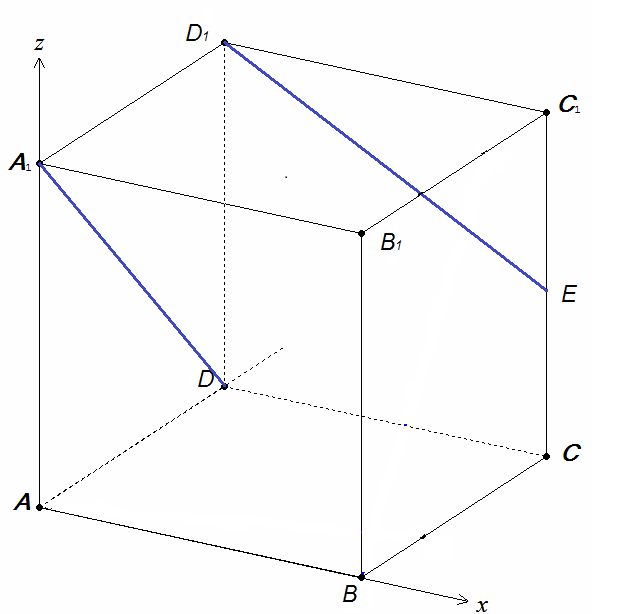
Введем прямоугольную систему координат, как указано на рисунке. Найдем координаты точки Е (1;1;  ) и координаты направляющих векторов прямых A1D и D1E:
) и координаты направляющих векторов прямых A1D и D1E: 
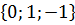 ,
, 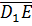 =
=  .
.
Косинус угла 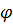 между прямыми А1 D и D 1 E определяется по формуле (1):
между прямыми А1 D и D 1 E определяется по формуле (1):
 =
=  ,
, 
Ответ: 






