Гипербола – геометрическое место точек на плоскости, разность расстояний которых по модулю от двух фиксированных точек (фокусов), есть величина постоянная (рис. 2.31).
Рис. 2.31
Итак, имеем
(2.75)
Рационализируя это уравнение, получим каноническое уравнение эллипса в виде
(2.76)
где 
так как 
Пример 2.26. Составить уравнение гиперболы, если известно, что еe фокусы расположены на оси 
и 
Решение. Из условий задачи имеем
Тогда уравнение гиперболы будет иметь вид 
Ответ: 
Каноническое уравнение параболы.
Парабола – геометрическое место точек на плоскости, для которых расстояния до некоторой прямой (директрисой) и до фиксированной точки (фокуса) равны (рис. 2.32).
Рис. 2. 32
Итак, согласно определению имеем
Рационализируя это уравнение, получим каноническое уравнение параболы в виде
где 
называется параметром параболы.
Пример 2.27. Написать уравнение параболы, если она симметрична относительно оси 
, проходит через точку 
и вершина совпадает с началом координатной системы.
Решение. Так как точка 
принадлежит параболе, то координаты этой точки удовлетворяют уравнению параболы 
Подставляя координаты точки 
в уравнение параболы, получим
Тогда уравнение параболы будет иметь вид 
Ответ: 
Задачи с ответами.
2.7.1. Найти решение линейной неоднородной системы по правилам Крамера
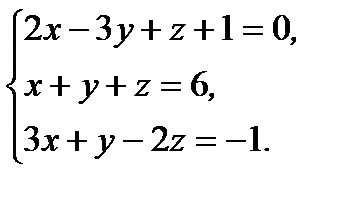
Ответ: 
2.7.2. Даны векторы 
и 
. Найти их скалярное произведение 
Ответ: 
2.7.3. С помощью векторного произведения найти площадь параллелограмма, сторонами которого являются векторы 
Ответ: 
2.7.4. Вычислить смешанное произведение 
Ответ: 
2.7.5. Даны координаты начала 
и конца 
отрезка 
Где строить универсам между 
и 
(точка 
), чтобы суммарная длина пути была одинакова для жителей обоих микрорайонов и в случаях: 1. Населения микрорайонов одинаковы. 2. Население микрорайона с центром в в 
раз больше населения микрорайона с центром в .
Ответ: 1. 
2. 
2.7.6. Предприятие предусматривает выпустить продукции трех видов в количестве 
единиц, которые принесут прибыль в 40, 60, 80 рублей с единицы. 1. Определить так, чтобы прибыль предприятия равнялась 600 рублям. 2. Предполагая, что при изменении технологии прибыль на единицу продукции изменится и составит соответственно 20, 50, 70 рублей с единицы, определить производственные программы, дающие при разных технологиях одинаковую прибыль, равную 600 рублям.
Ответ: 1. 
2. 
2.7.7. На предприятии постоянные общие издержки производства составляют 4000 рублей, а переменные издержки на единицу продукции – 500 рублей. Определить себестоимость 
одной единицы продукции как функцию объема производства 
Ответ: 
2.7.8. Найти длины осей, координаты фокусов и эксцентриситет эллипса, заданного уравнением: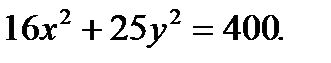 
Ответ: 
и 
и 
; 
2.7.9. Фокусы гиперболы совпадают с фокусами эллипса 
Составить уравнение гиперболы, если ее эксцентриситет 
Ответ: 
2.7.10. Определить точки пересечения эллипса 
и параболы 
Ответ: 
и 
