Ниже перейдем к нахождению экстремумов функции двух переменных, аргументы которой удовлетворяют условию связи. Пусть имеем функцию двух переменных  Нужно найти экстремумы этой функции при условии связи
Нужно найти экстремумы этой функции при условии связи
 (4.24)
(4.24)
то есть нужно исследовать функцию  на условный экстремум методом Лагранжа. Суть метода состоит в том, что составляем функцию Лагранжа
на условный экстремум методом Лагранжа. Суть метода состоит в том, что составляем функцию Лагранжа  где
где 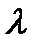 пока неопределенный множитель Лагранжа и эту функцию исследуем на экстремум, пользуясь необходимым условием экстремума (4.21) и условием связи (4.24). Итак, имеем
пока неопределенный множитель Лагранжа и эту функцию исследуем на экстремум, пользуясь необходимым условием экстремума (4.21) и условием связи (4.24). Итак, имеем
 (4.25)
(4.25)
Решая систему уравнений (4.25) относительно трех неизвестных  , найдем
, найдем  и точки возможного экстремума (стационарные точки). Далее с помощью достаточных условий исследуем каждую стационарную точку на экстремум.
и точки возможного экстремума (стационарные точки). Далее с помощью достаточных условий исследуем каждую стационарную точку на экстремум.
Пример 4.13. ( пример экономического характера) Пусть функция полезности имеет вид,  где
где  количество единиц первого товара,
количество единиц первого товара,  количество единиц второго товара. Потребитель имеет возможность потратить всего 1200 денежных единиц на приобретение
количество единиц второго товара. Потребитель имеет возможность потратить всего 1200 денежных единиц на приобретение  единиц первого товара, цена единицы которого составляет 1 денежную единицу, и
единиц первого товара, цена единицы которого составляет 1 денежную единицу, и  единиц второго товара, цена единицы которого составляет 4 денежных единиц. Найти значения
единиц второго товара, цена единицы которого составляет 4 денежных единиц. Найти значения  и
и  при которых полезность будет наибольшей.
при которых полезность будет наибольшей.
Решение. Очевидно, что функция Лагранжа имеет вид:

Тогда, согласно (4.25) имеем
Тогда функция Лагранжа принимает вид
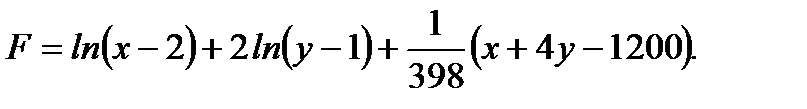
Проводя исследование полученной функции  на обычный экстремум в точке с координатами
на обычный экстремум в точке с координатами 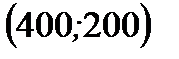 , получим, что исходная функция имеет max, при этом
, получим, что исходная функция имеет max, при этом 
Ответ: Полезность будет наибольшей при 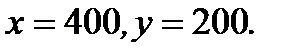
Задачи с ответами.
4.5.1. 

Ответ:  ;
;  ;
; 
4.5.2. Найти частные производные третьего порядка от функции

Ответ: 
4.5.3. Исследовать на экстремум функцию
 .
.
Ответ: 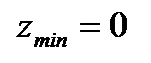 в точке
в точке 
4.5.4. Исследовать на экстремум функцию
 .
.
Ответ:  в точке
в точке 
4.5.5. Исследовать на условный экстремум функцию
 при условии
при условии 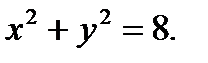
Ответ:  в точках
в точках  и
и  ,
,  в точках
в точках  и
и  .
.
4.5.6. Пусть функция полезности имеет вид 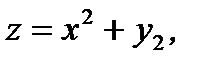 где
где  количество единиц первого товара,
количество единиц первого товара,  количество единиц второго товара. Потребитель имеет возможность потратить всего
количество единиц второго товара. Потребитель имеет возможность потратить всего  денежных единиц на приобретение
денежных единиц на приобретение  единиц первого товара, цена единицы которого составляет 1 денежную единицу, и
единиц первого товара, цена единицы которого составляет 1 денежную единицу, и  единиц второго товара, цена единицы которого составляет 2 денежных единиц. Найти значения
единиц второго товара, цена единицы которого составляет 2 денежных единиц. Найти значения  и
и  при которых полезность будет наибольшей.
при которых полезность будет наибольшей.
Ответ:  при
при 
4.5.7. Найти производную  от функции
от функции  , если
, если 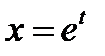 ,
, 
Ответ: 
4.5.8. Найти  от функции
от функции 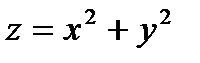 в точке
в точке 
Ответ: 
4.5.9. Найти производные  ,
,  от функции
от функции  , если
, если  ,
,  .
.
Ответ: 

4.5.10. Дано 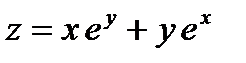 . Показать, что функция
. Показать, что функция  удовлетворяет соотношению
удовлетворяет соотношению 
 Нужно найти экстремумы этой функции при условии связи
Нужно найти экстремумы этой функции при условии связи (4.24)
(4.24) на условный экстремум методом Лагранжа. Суть метода состоит в том, что составляем функцию Лагранжа
на условный экстремум методом Лагранжа. Суть метода состоит в том, что составляем функцию Лагранжа  где
где 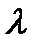 пока неопределенный множитель Лагранжа и эту функцию исследуем на экстремум, пользуясь необходимым условием экстремума (4.21) и условием связи (4.24). Итак, имеем
пока неопределенный множитель Лагранжа и эту функцию исследуем на экстремум, пользуясь необходимым условием экстремума (4.21) и условием связи (4.24). Итак, имеем (4.25)
(4.25) , найдем
, найдем  и точки возможного экстремума (стационарные точки). Далее с помощью достаточных условий исследуем каждую стационарную точку на экстремум.
и точки возможного экстремума (стационарные точки). Далее с помощью достаточных условий исследуем каждую стационарную точку на экстремум. где
где  количество единиц первого товара,
количество единиц первого товара,  количество единиц второго товара. Потребитель имеет возможность потратить всего 1200 денежных единиц на приобретение
количество единиц второго товара. Потребитель имеет возможность потратить всего 1200 денежных единиц на приобретение  единиц первого товара, цена единицы которого составляет 1 денежную единицу, и
единиц первого товара, цена единицы которого составляет 1 денежную единицу, и  единиц второго товара, цена единицы которого составляет 4 денежных единиц. Найти значения
единиц второго товара, цена единицы которого составляет 4 денежных единиц. Найти значения  и
и  при которых полезность будет наибольшей.
при которых полезность будет наибольшей. 
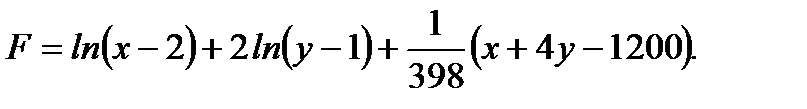
 на обычный экстремум в точке с координатами
на обычный экстремум в точке с координатами 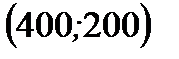 , получим, что исходная функция имеет max, при этом
, получим, что исходная функция имеет max, при этом 
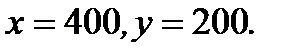


 ;
;  ;
; 


 .
.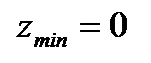 в точке
в точке 
 .
. в точке
в точке 
 при условии
при условии 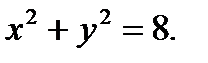
 в точках
в точках  и
и  ,
,  в точках
в точках  и
и  .
.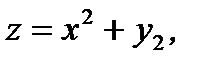 где
где  количество единиц первого товара,
количество единиц первого товара,  количество единиц второго товара. Потребитель имеет возможность потратить всего
количество единиц второго товара. Потребитель имеет возможность потратить всего  денежных единиц на приобретение
денежных единиц на приобретение  единиц первого товара, цена единицы которого составляет 1 денежную единицу, и
единиц первого товара, цена единицы которого составляет 1 денежную единицу, и  единиц второго товара, цена единицы которого составляет 2 денежных единиц. Найти значения
единиц второго товара, цена единицы которого составляет 2 денежных единиц. Найти значения  и
и  при которых полезность будет наибольшей.
при которых полезность будет наибольшей.  при
при 
 от функции
от функции  , если
, если 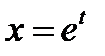 ,
, 

 от функции
от функции 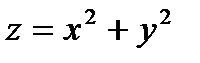 в точке
в точке 

 ,
,  от функции
от функции  , если
, если  ,
,  .
.

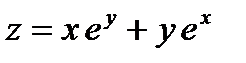 . Показать, что функция
. Показать, что функция  удовлетворяет соотношению
удовлетворяет соотношению 






